If (ik<is) or (jk<js) then

Пример 1.

В прямоугольной матрице поменять местами строки, содержащие максимальный и минимальный ее элементы.

По условию задачи не требуется определять положение максимального и минимального элементов в строке. Поэтому в программе используются лишь переменные и 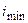, отмечающие номера строк, содержащих эти элементы. Если 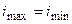, обмен строк не производится (нет смысла менять строку саму с собой).

Program Task201;

Const Mmax = 20; Nmax = 15;

Type Matrix = array [1..Mmax,1..Nmax] of real;

Var i,j,m,n,imax,imin: byte;

Amax,Amin,R: real;

A: Matrix;

Begin

В в о д m, n, A

Amax:=a[1,1]; imax:=1;

Amin:=a[1,1]; imin:=1;

For i:=1 to m do { Поиск в матрице }

For j:=1 to n do { максимального и }

If a[i,j]>Amax then { минимального }

Begin { элементов }

Amax:=a[i,j]; imax:=i;

End

Else

Ifa[i,j]<Amin then

Begin

Amin:=a[i,j]; imin:=i;

End;

If imax<>imin then

For j:=1 to n do { Обмен строк матрицы }

Begin

R:=a[imin,j]; a[imin,j]:=a[imax,j]; a[imax,j]:=R

End;

Печать A

End.

Пример 2.

Найти максимальный элемент среди элементов квадратной матрицы, расположенных выше главной диагонали, и минимальный элемент среди тех элементов, которые расположены ниже главной диагонали, после чего найденные элементы обменять местами.

Выпишем в явном виде элементы, расположенные выше главной диагонали (верхний треугольник квадратной матрицы):

a[1,2] a[1,3] a[1,4]... a[1,n-1] a[1,n]

a[2,3] a[2,4]... a[2,n-1] a[2,n]

a[3,4]... a[3,n-1] a[3,n]

...............................

a[n-2,n-1] a[n-2,n]

a[n-1,n]

Для общего элемента 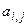номер строки изменяется от 1 до n-1, т.е. i = 1.. (n-1); номер столбца - от i+1 до n, т.е. j = (i+1).. n.

Аналогично для элементов нижнего треугольника:

a[2,1]

a[3,1] a[3,2]

a[4,1] a[4,2] a[4,3]

.......................

a[n,1] a[n,2] a[n,3]... a[n,n-2] a[n,n-1]

Здесь i = 2.. n, j = 1.. (i-1).

Program Task202;

Const Nmax = 20;

Type Matrix = array [1..Nmax,1..Nmax] of real;

Var i,j,n,imax,imin,jmax,jmin: byte;

Amax,Amin: real;

A: Matrix;

Begin

В в о д n, A

Amax:=a[1,2]; imax:=1; jmax:=2;

For i:=1 to n-1 do { Поиск максимального }

For j:=i+1 to n do { элемента выше }

If a[i,j]>Amax then { главной диагонали }

Begin

Amax:=a[i,j]; imax:=i; jmax:=j

End;

Amin:=a[2,1]; imin:=2; jmin:=1;

For i:=2 to n do { Поиск минимального }

For j:=1 to i-1 do { элемента ниже }

If a[i,j]<Amin then { главной диагонали }

Begin

Amin:=a[i,j]; imin:=i; jmin:=j

End;

a[imin,jmin]:=Amax; a[imax,jmax]:=Amin;

Печать A

End.

Пример 3.

Среди диагоналей квадратной матрицы, параллельных главной и расположенных выше нее (включая главную диагональ), найти такую, сумма модулей элементов которой максимальная.

Индексы элементов, входящих в рассматриваемые диагонали:

1,1 2,2 3,3 4,4... n-2,n-2 n-1,n-1 n,n

1,2 2,3 3,4 4,5... n-2,n-1 n-1,n

1,3 2,4 3,5 4,6... n-2,n

.......................................

1,n-1 2,n

1,n

Будем считать номер диагонали k равным номеру столбца ее начального элемента: 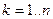. Тогда индексы элементов, входящих в k-ую диагональ, равны j = k.. n; i = j - k +1.

Program Task203;

Const Nmax = 20;

Type Matrix = array [1..Nmax,1..Nmax] of real;

SumType = array [1..Nmax] of real;

Var i,j,k,kmax,n: byte;

SumMax: real;

A: Matrix;

S: SumType;

Begin

В в о д n, A

For k:=1 to n do { Формирование массива S, }

Begin { содержащего суммы }

S[k]:=0; { элементов диагоналей }

For j:=k to n do

Begin

i:=j-k+1; S[k]:=S[k]+abs(a[i,j]);

End;

SumMax:=S[1]; kmax:=1;

For k:=2 to n do { Определение максимального }

If S[k]>SumMax then { значения в массиве S }

Begin

SumMax:=S[k]; kmax:=k

End;

П е ч а т ь SumMax, kmax

End.

Примечание. Нетрудно заметить, что для диагоналей, параллельных главной, соблюдается следующая закономерность между индексами их элементов: j - i = k - 1, где k - номер диагонали.

Используя эту закономерность, программу можно организовать следующим образом:

- обнулить элементы массива S;

- перебирая все элементы матрицы, расположенные выше главной диагонали и на главной диагонали (по циклу i = 1.. n, j = i.. n), модуль очередного элемента 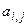добавлять к сумме ;

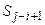- определить порядковый номер максимального элемента в одномерном массиве S.

Пример 4.

Побочной диагональю квадратной матрицы называют диагональ, соединяющую левый нижний угол матрицы с ее верхним правым углом. Среди диагоналей, параллельных побочной и расположенных ниже нее, найти такую, среднее арифметическое значение элементов которой максимальное.

Индексы элементов, входящих в рассматриваемые диагонали:

n,2 n-1,3 n-2,4... 4,n-2 3,n-1 2,n

n,3 n-1,4 n-2,5... 4,n-1 3,n

n,4 n-1,5 n-2,6... 4,n

.......................................

n,n-1 n-1,n

n,n

Будем считать номер диагонали k равным номеру столбца ее начального элемента: . Тогда индексы элементов, входящих в k-ую диагональ, равны i = n.. k; j = n - i+k. Количество элементов в диагонали равно n-k+1.

Program Task204;

Const Nmax = 20;

Type Matrix = array [1..Nmax,1..Nmax] of real;

Ar = array [2..Nmax] of real;

Var i,j,k,kmax,n: byte;

ArMax: real;

A: Matrix;

Sar: Ar;

Begin

В в о д n,A

For k:=2 to n do { Формирование массива Sar, }

Begin { содержащего средние }

Sar[k]:=0; { арифметические значения }

For i:=n downto k do { элементов диагоналей }

Begin

j:=n-i+k; Sar[k]:=Sar[k]+a[i,j];

End;

Sar[k]:=Sar[k]/(n-k+1);

End;

ArMax:=Sar[2]; kmax:=2;

For k:=3 to n do { Определение }

If Sar[k]>ArMax then { максимального }

Begin { значения в массиве Sar }

ArMax:=Sar[k]; kmax:=k

End;

П е ч а т ь ArMax, kmax

End.

Примечание. Для диагоналей, параллельных побочной, соблюдается следующая закономерность между индексами их элементов: i + j = n + k, где k - номер диагонали. Используя эту закономерность, программу можно организовать аналогично рекомендациям, отраженным в примечании к задаче 3.

Пример 5.

Расположить элементы прямоугольной матрицы в обратном порядке.

В программе Task205 сначала переставляются в обратном порядке строки матрицы, а затем - ее столбцы.

Program Task205;

Const Mmax = 20; Nmax = 15;

Type Matrix = array [1..Mmax,1..Nmax] of real;

Var i,j,k,m,n: byte;

R: real;

A: Matrix;

Begin

В в о д m, n, A

i:=1; k:=m; { Перестановка строк матрицы }

While i<k do { в обратном порядке }

Begin

For j:=1 to n do

Begin

R:=a[i,j]; a[i,j]:=a[k,j]; a[k,j]:=R;

End;

Inc(i); Dec(k);

End;

j:=1; k:=n; { Перестановка столбцов матрицы }

While j<k do { в обратном порядке }

Begin

For i:=1 to m do

Begin

R:=a[i,j]; a[i,j]:=a[i,k]; a[i,k]:=R;

End;

Inc(j); Dec(k);

End;

Печать A

End.

Пример 6.

Найти максимальное из чисел, встречающихся в целочисленной прямоугольной матрице более одного раза.

Функция RepElem в программе Task206 определяет, является ли элемент с индексами i и j повторяющимся в матрице A. Если RepElem(i, j) = true и Cond = true (повторяющийся элемент встретился впервые), то переменные запоминают индексы, а переменная - значение этого элемента. При Cond = false изменение значений переменных , , производится, если новый повторяющийся элемент превышает значение .

Program Task206;

Const Mmax = 30; Nmax = 50;

Type Matrix = array [1..Mmax,1..Nmax] of integer;

Var m,n, { размер матрицы }

imax,jmax, { позиция макс.элемента }

i,j,is,js: byte;

Amax: integer; { значение макс.элемента }

Cond: boolean;

A: Matrix; { исходная матрица }

{ -------------------------------------------- }

Function RepElem(ik,jk:byte):boolean;

{ RepElem=true, если элемент a[ik,jk] повторяющийся }

Var i,j,is,js: byte;

R: integer;

Begin

R:=a[ik,jk]; RepElem:=false;

For i:=1 to m do

For j:=1 to n do

If (R=a[i,j]) and (i<>ik) and (j<>jk) then

Begin

RepElem:=true; Exit

End;

End { RepElem };

{ -------------------------------------------- }

Begin

imax:=0; jmax:=0; Amax:=0; Cond:=true;

For i:=1 to m do

For j:=1 to n do

Begin

If RepElem(i,j) then

IfCond then

Begin

imax:=i; jmax:=j;

Amax:=a[i,j]; Сond:=false

End

Else

Ifa[i,j]>Amax then

Begin

imax:=i; jmax:=j; Amax:=a[i,j];

End

End;

Writeln('imax = ',imax,' jmax = ',jmax,' Amax = ',Amax);

End.

Пример 7.

Элементам целочисленной квадратной матрицы присвоить значения натурального ряда чисел в порядке прохождения правосторонней спирали, начиная с заданного углового элемента.

Например, для матрицы 6-го порядка с начальным элементом (1,6) имеем:

16 17 18 19 20 1

15 30 31 32 21 2

14 29 36 33 22 3

13 28 35 34 23 4

12 27 26 25 24 5

11 10 9 8 7 6

Program Task207;

{ Нумерация углов матрицы: 1 - левый верхний; 2 - правый }

{ верхний; 3 - правый нижний; 4 - левый нижний }

Const Nmax = 30;

Type Matrix = array [1..Nmax,1..Nmax] of word;

Var n, { размер матрицы А }

i,j,

k, { условный номер угла матрицы }

is, { индекс нач.эл-та формируемой части строки }

ik, { то же для конечного элемента строки }

js, { индекс нач.эл-та формируемой части столбца }

jk: byte; { то же для конечного элемента столбца }

Number: word; { заполняемое значение }

Cond: boolean;

A: Matrix;

{ ---------------------------------------------- }

Procedure ToRight;

{ Движение вправо по строке }

Var j: byte;

Begin

For j:=js to jk do

Begin

a[is,j]:=Number; Inc(Number);

End;

End { ToRight };

{ ---------------------------------------------- }

Procedure ToDown;

{ Движение вниз по столбцу }

Var i: byte;

Begin

For i:=is to ik do

Begin

a[i,jk]:=Number; Inc(Number);

End;

End { ToDown };

{ ---------------------------------------------- }

Procedure ToLeft;

{ Движение влево по строке }

Var j: byte;

Begin

For j:=jk downto js do

Begin

a[ik,j]:=Number; Inc(Number);

End;

End { ToLeft };

{ ---------------------------------------------- }

Procedure ToUp;

{ Движение вверх по столбцу }

Var i: byte;

Begin

For i:=ik downto is do

Begin

a[i,js]:=Number; Inc(Number);

End;

End { ToUp };

{ ---------------------------------------------- }

Begin

Ввод размера матрицы n и номера начального угла k

Number:=1; Cond:=true;

is:=1; js:=1; ik:=n; jk:=n;

While Cond do

Begin

Case k of

1: Begin

ToRight; Inc(is);

End;

2: Begin

ToDown; Dec(jk);

End;

3: Begin

ToLeft; Dec(ik);

End;

4: Begin

ToUp; Inc(js);

End;

end;

Inc(k);

If k>4 then k:=1;

If (ik<is) or (jk<js) then

Cond:=false;

End;

End.

Пример 8.

Элементы целочисленной прямоугольной матрицы A строго упорядочены по возрастанию:

a[1,1] < a[1,2] < a[1,3] <... < a[1,n] < a[2,1] <...

... < a[2,n] < a[3,1] <... < a[m,n]

Найти элемент, равный заданному числу , и отпечатать его индексы. Число действий в решении должно быть порядка , а не .

Последнее ограничение означает, что последовательный перебор всех элементов матрицы не допускается.

Вариант 1.

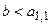Если или 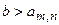, то матрица не содержит элемента, равного значению . В противном случае будем сравнивать переменную с первым элементом каждой строки матрицы. Если , = 2.. , то элемент, равный , может находиться в строке -1. Тогда производится последовательный просмотр элементов ( -1)-ой строки. Если условие ни разу не было выполнено, то просматриваются элементы m-ой строки.