Лекция 4
Раздел 3. Матрицы.
Первоначальные сведения о матрице.
Определение 1. Прямоугольной, или  - матрицей называется совокупность
- матрицей называется совокупность  чисел
чисел  , расположенных в виде прямоугольной таблицы из т строк и п столбцов:
, расположенных в виде прямоугольной таблицы из т строк и п столбцов:
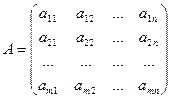 . (1)
. (1)
Размер матрицы А обозначается символом:  . Числа
. Числа  называются элементами матрицы А. У элемента
называются элементами матрицы А. У элемента  первый индекс
первый индекс 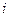 указывает номер строки, а второй индекс j – номер столбца, на пересечении которых находится этот элемент в матрице.
указывает номер строки, а второй индекс j – номер столбца, на пересечении которых находится этот элемент в матрице.
Например, матрица

имеет размер  , её элемент
, её элемент  , принадлежащий 3-ей строке и 1-му столбцу, равен
, принадлежащий 3-ей строке и 1-му столбцу, равен  .
.
Определение 2. Матрица называется комплексной, если хотя бы один ее элемент является комплексным числом, и действительной, если все ее элементы – действительные числа.
Пример.
 - комплексная матрица,
- комплексная матрица,  - действительная матрица.
- действительная матрица.
В учебной и математической литературе встречаются следующие обозначения матриц:  ,
,  ,
, 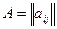 , где
, где  ,
,  . (Запись
. (Запись  означает, что
означает, что  )
)
Матрицы А и В имеют одинаковый размер, т.е.  , если они содержат равное количество строк и столбцов.
, если они содержат равное количество строк и столбцов.
Определение 3. Матрицы А и В называются равными, если  , и их соответствующие элементы равны, т.е.
, и их соответствующие элементы равны, т.е.  ,
,  ,
,  . В таких случаях пишут
. В таких случаях пишут 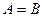 .
.
Матрица, состоящая из одной строки, называется матрицей-строкой:
 ,
, 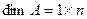 .
.
Матрица, имеющая лишь один столбец, называется матрицей-столбцом:
 ,
,  .
.
Матрица, состоящая из нулей, называется нулевой. Нулевые матрицы разных размеров принято обозначать одним и тем же символом О, что не приводит к недоразумениям.
Линейные действия над матрицами.
Определение 1. Пусть матрицы А, В и С такие, что  . Суммой матриц А и В называется такая матрица
. Суммой матриц А и В называется такая матрица  , элементы которой определяются равенствами
, элементы которой определяются равенствами 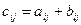 , где
, где  ,
,  .
.
Пример.
а) 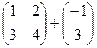 - сложение не имеет смысла, т.к. матрицы разного размера;
- сложение не имеет смысла, т.к. матрицы разного размера;
б)  .
.
Определение 2. Матрица  называется противоположной матрицей к матрице А, если
называется противоположной матрицей к матрице А, если  и каждый элемент матрицы
и каждый элемент матрицы  есть элемент матрицы А, взятый с противоположным знаком.
есть элемент матрицы А, взятый с противоположным знаком.
Пример. Если 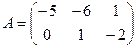 , то противоположная матрица
, то противоположная матрица  .
.
Свойства операции сложения матриц.
Для матриц А, В, С, О таких, что  , справедливы следующие утверждения:
, справедливы следующие утверждения:
1.  (сложение матриц коммутативно);
(сложение матриц коммутативно);
2.  (сложение матриц ассоциативно);
(сложение матриц ассоциативно);
3.  (свойство нулевой матрицы);
(свойство нулевой матрицы);
4.  .
.
Сложение матриц обладает обратной операцией – вычитанием.
Определение 3. Пусть матрицы А, В и С такие, что  . Разностью матриц А и В называется такая матрица
. Разностью матриц А и В называется такая матрица  , элементы которой определяются равенствами
, элементы которой определяются равенствами  , где
, где  ,
,  .
.
Пример.
а) 
б)  - вычитание не имеет смысла, т.к. матрицы разного размера.
- вычитание не имеет смысла, т.к. матрицы разного размера.
Определение 4. Пусть матрицы А и В такие, что 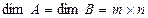 . Произведением матрицы А на число l называется матрица
. Произведением матрицы А на число l называется матрица 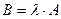 , элементы которой определяются равенствами:
, элементы которой определяются равенствами:  , где
, где  ,
,  .
.
Пример.

Свойства операции умножения матрицы на число.
Для матриц А и В таких, что  , и любых действительных чисел a и b справедливы равенства:
, и любых действительных чисел a и b справедливы равенства:
1.  ;
;
2.  ;
;
3.  ;
;
4. 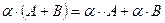 .
.
Умножение матриц.
Определение 1. Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В, т.е.  ,
, 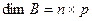 .
.
Из согласованности матрицы А с матрицей В, не следует согласованность матрицы В с матрицей А.
Пример.
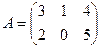 ,
,  .
.
Матрица А согласована с матрицей В (А имеет 3 столбца, В – 3 строки), но матрица В не согласована с матрицей А (В имеет 3 столбца, А – 3 строки).
Определение 2. Пусть матрица А согласована с матрицей В, т.е.  ,
, 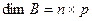 . Произведением матрицы А на матрицу В называется матрица
. Произведением матрицы А на матрицу В называется матрица  , размер которой равен
, размер которой равен  , а элементы вычисляются по формулам:
, а элементы вычисляются по формулам:
 ,
,  ;
;  .
.
Пример.
1)  ,
,
 . В этом примере произведение
. В этом примере произведение  определено, а произведение
определено, а произведение  не определено, т.к. число столбцов матрицы В не равно числу строк матрицы А.
не определено, т.к. число столбцов матрицы В не равно числу строк матрицы А.
Оба произведения  и
и  определены, если
определены, если  ,
,  .
.
Пример. Для матриц  и
и  определены произведения
определены произведения  и
и  , т.к.
, т.к.  ,
, 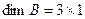 . Найдем произведение
. Найдем произведение  :
:
 ,
,  .
.
Вычислим  :
:
 ,
,  .
.
Из приведенных примеров видно, что если даже оба произведения  и
и  имеют смысл, то эти произведения могут оказаться не одинаковыми, т.е. умножение матриц не обладает свойством коммутативности.
имеют смысл, то эти произведения могут оказаться не одинаковыми, т.е. умножение матриц не обладает свойством коммутативности.
Свойства операции умножения матриц.
1.  ;
;
2.  ;
;
3. 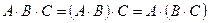 .
.
Эти свойства доказываются непосредственной проверкой. Докажем, например, свойство 3. Пусть  ,
, 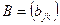 ,
,  . По определению произведения матриц элементами произведений
. По определению произведения матриц элементами произведений  и
и  будут элементы
будут элементы  и
и  , а элементами двойных произведений
, а элементами двойных произведений  и
и  - соответственно элементы
- соответственно элементы  и
и  . Таким образом, соответствующие элементы матриц
. Таким образом, соответствующие элементы матриц  и
и  равны. Следовательно, сами эти матрицы равны.
равны. Следовательно, сами эти матрицы равны.
3.4 Операции над матрицами: транспонирование, комплексное сопряжение, сопряжение по Эрмиту.
Определение 1. Транспонированием матрицы А называется операция замены каждой ее строки столбцом с тем же номером. Полученную в результате этой операции матрицу называют транспонированной к матрице А и обозначают через  .
.
Если А – матрица размера  , то
, то  - матрица размера
- матрица размера  .
.
Пример.  ,
,  .
.
Запишем транспонированную матрицу:  ,
,  .
.
Определение 2. Комплексным сопряжением матрицы А называется операция замены каждого элемента матрицы А на комплексно сопряженный ему элемент. Матрица, полученная в результате этой операции, называется комплексно сопряженной с матрицей А и обозначается  .
.
Пример. Пусть  .
.
Представим все элементы матрицы А в алгебраической форме
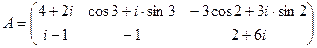 ,
,
тогда комплексно сопряженная матрица имеет вид
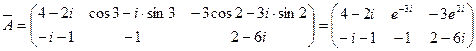 .
.
Определение 3. Сопряженим по Эрмиту матрицы А называется операция сочетающая транспонирование и комплексное сопряжение. Матрица, полученная в результате этой операции, называется эрмитово-сопряженной с матрицей А и обозначается  , т.е.
, т.е.  .
.
Пример. Пусть  ,
,
тогда  и
и  .
.
Для всех трех операций, непосредственной проверкой, можно доказать следующие свойства:
I. II.
1) 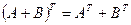 ; 4)
; 4)  ;
;
2)  ; 5)
; 5)  ;
;
3)  ; 6)
; 6)  ;
;
III. IV.
7) 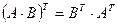 ; 10)
; 10) 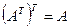 ;
;
8)  ; 11)
; 11) 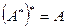 .
.
9)  ;
;
3.5 Квадратные матрицы.
Определение 1. Квадратной матрицей называется матрица А, у которой число строк равно числу столбцов, т.е.  .
.
В квадратной матрице совокупность элементов на линии, соединяющей верхний левый угол с правым нижним, называют главной диагональю. У элементов главной диагонали номер строки совпадает с номером столбца. Например, у матрицы размера  элементы
элементы  образуют главную диагональ.
образуют главную диагональ.
Определение 2. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, т.е.

называют диагональными.
Диагональная матрица, у которой все элементы главной диагонали одинаковые, называется скалярной. Частным случаем скалярных матриц является единичная матрица
 .
.
Легко видеть, что  .
.
Определение 3. Квадратную матрицу называют треугольной, если все ее элементы, стоящие выше (или ниже) главной диагонали, равны нулю. При этом матрицу вида

называют верхней треугольной матрицей, а матрицу вида

- нижней треугольной матрицей.
Определение 4. Квадратную матрицу А называют симметрической, если она не меняется при транспонировании, т.е.  .
.
Например, рассмотрим матрицу  . Так как транспонированная матрица имеет вид:
. Так как транспонированная матрица имеет вид: 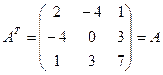 , то матрица А симметрическая.
, то матрица А симметрическая.
Определение 5. Квадратная матрица А называется кососимметрической, если при транспонировании она меняет свой знак, т.е.  .
.
Например, для матрицы  , транспонированная матрица имеет вид:
, транспонированная матрица имеет вид:  , поэтому матрица А кососимметрическая.
, поэтому матрица А кососимметрическая.
Определение 5. Квадратная матрица называется эрмитовой, если она равна эрмитово-сопряженной, т.е.  .
.
Определение 6. Квадратная матрица называется ортогональной, если ее произведение на
транспонированную матрицу равно единичной матрице, т.е.
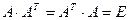 .
.
Определение 7. Квадратная матрица называется унитарной, если ее произведение на
эрмитово-сопряженную матрицу равно единичной матрице, т.е.
 .
.
При помощи матриц изучаются свойства различных устройств в электротехнике и технике сверхвысоких частот (СВЧ).
В частности, в технике сверхвысоких частот (СВЧ) применяют матрицу рассеяния S, связывающую амплитуды волн, бегущих к устройству  и амплитуды волн, бегущих от устройства
и амплитуды волн, бегущих от устройства  :
:
 ,
,
где п – число каналов, по которым волны бегут к устройству или от него. В теории устройств СВЧ доказывается, что необходимым и достаточным условием отсутствия потерь в устройстве служит унитарность матрицы рассеяния.
Пример. Проверить, обладает ли потерями устройство, описываемое матрицей рассеяния
 .
.
Решение. Проверим, будет ли матрица S унитарной.
1. Ищем эрмитово-сопряженную матрицу.
 Þ
Þ 
2. Проверяем равенство  .
.







