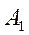Транспортная задача
Рассмотрим так называемую транспортную задачу по критерию стоимости. Данная задача используется для оптимизации планирования грузоперевозок.
Постановка задачи
1. В m пунктах отправления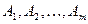 
, которые будем в дальнейшем называть поставщиками, сосредоточено определенное количество единиц некоторого однородного продукта, которое обозначим 
.
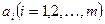Однородный – одного вида (например: пищевые продукты, одежда, обувь, ткани).
2. Данный продукт потребовался в n пунктах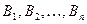 
, которые будем называть потребителями. Объем потребителя обозначим 
.
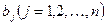3. Известны расходы на перевозку единицы продукта из пункта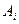 
в пункт 
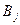, которые равны 
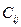и приведены в матрице транспортных расходов 
.
4. Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором
1) весь продукт вывозится из пунктов в пункты в соответствии с потребностью
2) общая величина транспортных издержек будет минимальной.
|
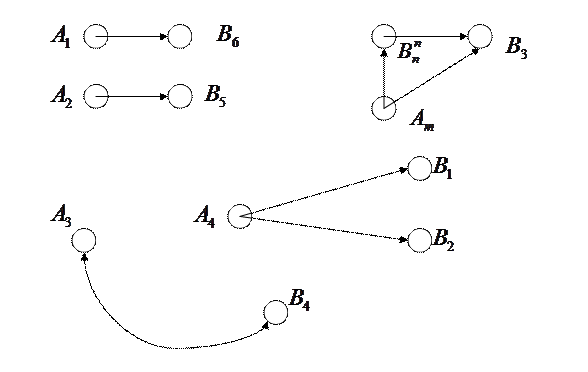
Обозначим количество продукта, перевозимого из пункта 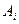в пункт 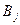через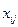 
. Тогда получим матрицу перевозок 
.
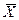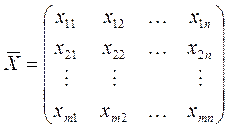
А также матрицу стоимости перевозок (иногда ее называют «матрицей тарифов»)
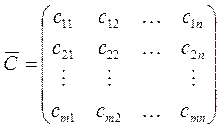
Тогда целевая функция задачи имеет вид
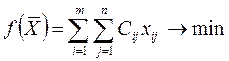(1)
а ограничения выделяют следующим образом:
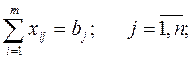(2)
(Условие по потребности)
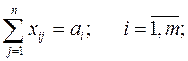(3)
(Условие по запасам)
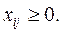(4)
Необходимым и достаточным условием того чтобы задача имела решение, является условие баланса:
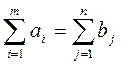(5)
Транспортная задача, в которой имеет место равенство (5) называется закрытой.
Решение транспортной задачи состоит из 2-х этапов:
1) Нахождение первоначального опорного плана.
2) Нахождение оптимального плана перевозок по методу потенциалов.
Виды моделей транспортной задачи
Модель транспортной задачи включает в себя: целевую функцию (1) и систему ограничений (2), (3) и (4).
Модель транспортных задач бывает 2-х типов.
1. Закрытая модель .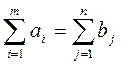
Для того чтобы решать транспортную задачу ее необходимо привезти к закрытому виду.
Для закрытых моделей доказана теорема о существовании допустимого плана.
Теорема. Для того чтобы транспортная задача имела допустимые планы необходимо и достаточно, чтобы объем запасов совпадал с объемом потребностей.
2. Открытые модели:
2а)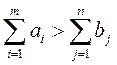 
Запасы превышают потребности
В этом случае вводится фиктивный потребитель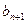 
, потребности которого равны 
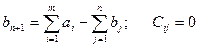. Стоимость перевозки единицы груза от поставщиков к 
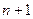-му потребителю равна 0.
2б)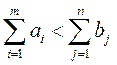 
Потребности превышают запасы
В этом случае вводится фиктивный поставщик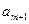 
. Запасы которого равны 
.
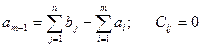Построение первоначального опорного плана
В транспортной задаче существуют понятия вырожденного и невырожденного плана.
План невырожденный, когда количество занятых клеток равно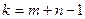 
, где m – число поставщиков, n – число потребителей.
План вырожденный, когда количество занятых клеток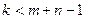 
.
Если план оказывается вырожденным, то следует часть свободных клеток условно считать занятыми. Для этого в них реально записываются нули, которые стоят там «негласно». Это делают в одной или нескольких клетках, исходя из требования, состоящего в том, что общее число занятых клеток должно быть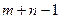 
. В дальнейшем с другими клетками обращаются как с занятыми.
| Поставщики | Потребители | Запасы | ||||
| 
| 
| … | 
| ||
| 
| 
| 
| |||
| 
| |||||
| 
| |||||
| … | … | |||||
| 
| 
| ||||
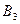
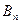
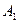
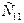
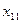
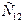
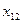
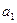
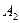
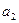
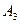
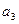
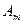
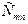
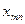
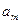
| Потребности |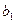 
| 
| 
| … | 
|
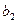
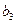
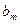
