Фдз 1. Матрицы. Операции над матрицами.
Операции с матрицами: равенство матриц; умножение матрицы на число; сложение матриц; перемножение матриц.
Транспонирование матрицы.
Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица.
Возведение квадратной матрицы в натуральную степень.
Фдз 2. Определители.
Определитель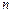 
-го порядка. Правила Саррюса вычисления определителей 2-го и 3-го порядков.
Основные свойства определителей.
Фдз 3. Определители (продолжение). Обратная матрица
Миноры и алгебраические дополнения.
Разложение определителя по строке (столбцу).
Обратная матрица, ее нахождение.
Фдз 4. Использование матриц и определителей при решении линейных алгебраических систем.
Совместные, несовместные линейные системы. Матричная запись линейной системы.
Невырожденные линейные системы.
Решение невырожденных систем по правилу Крамера и с помощью обратной матрицы.
Фдз 5. Метод Гаусса решения линейных алгебраических систем.
Приведение системы к треугольному виду.
Выделение свободных и базисных неизвестных.
Получение общего решения системы или вывода о несовместности системы.
Фдз 6. Векторы в,. Скалярное произведение векторов.
Вектор как направленный отрезок. Проекции вектора, длина вектора, направляющие косинусы.
Сложение векторов. Умножение вектора на число. Условие коллинеарности двух векторов.
Скалярное произведение векторов, его свойства, координатное выражение. Условие ортогональности двух векторов.
Фдз 7. Векторное и смешанное произведение векторов.
Компланарные, некомпланарные тройки векторов. Ориентация тройки векторов.
Векторное произведение: определение; свойства; координатное выражение.
Смешанное произведение: определение; свойства; координатное выражение. Условие компланарности тройки векторов.
Фдз 8. Прямая на плоскости.
Различные виды задания прямой на плоскости. Основные задачи по нахождению прямой на плоскости.
Взаимное расположение двух прямых. Угол между прямыми. Расстояние от точки до прямой.
Фдз 9. Плоскость и прямая в пространстве.
Общее уравнение плоскости. Нормальный вектор.
Прямая в пространстве: канонические, параметрические уравнения.
Фдз 10. Обзор основных задач занятий 1-9.
Фдз 11. Кривые второго порядка.
Эллипс. Каноническое уравнение. Полуоси, эксцентриситет, график.
Гипербола. Каноническое уравнение. Полуоси, эксцентриситет, асимптоты, график.
Парабола. Каноническое уравнение. Параметр параболы, график.
Фдз 12. Поверхности второго порядка.
Канонические уравнения эллипсоида, конуса, гиперболоидов, параболоидов, цилиндров.
Построение графиков поверхностей второго порядка по их сечениям плоскостями, параллельными координатным плоскостям.
Фдз 13. Комплексные числа.
Комплексные числа в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел.
Модуль, аргумент комплексного числа. Тригонометрическая и показательная формы записи комплексного числа.
Возведение в целую степень и извлечение корня из комплексного числа.
Фдз 14. Многочлены.
Корни многочлена, их кратность. Деление многочлена на многочлен (алгоритм Евклида). Целая и дробная части отношения двух многочленов.
Теорема Безу. Основная теорема алгебры многочленов.
Многочлены с действительными коэффициентами, их разложение на множестве действительных и комплексных чисел.
