Кодирование звуковой информации. Метод FM. Метод WT

В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды.

Т.о. при двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала.

Метод FM. Основан та том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот, каждый из которых представляет собой правильную синусоиду, а, следовательно, может быть описан числовыми параметрами, т.е. кодом. В природе звуковые сигналы имеют непрерывный спектр, т.е. являются аналоговыми. Их разложение в гармонические ряды и представление в виде дискретных цифровых сигналов выполняют специальный устройства — аналогово-цифровые преобразователи (АЦП)

Метод WT. Метод таблично волнового (Wave-Table) синтеза лучше соответствует современному уровню развития техники. В заранее подготовленных таблицах хранятся образцы звуков для множества различных музыкальных инструментах. В технике такие образцы называют сэмплами. Числовые коды выражают тип инструмента, номер его модели, высоту тона, продолжительность и интенсивность звука, динамику его изменения, некоторые параметры среды, в которой происходит звучание, а также прочие параметры, характеризующие особенности звучания. Поскольку в качестве образцов исполняются реальные звуки, то его качество получается очень высоким и приближается к качеству звучания реальных музыкальных инструментов.

 

15.Определение системы счисления, цифры, непозиционной и позиционной системы счисления, основания.

Система счисле́ния

Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимно-однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Множество символов, используемых для такого представления, называют цифрами.

В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.

В непозиционных системах любое число определяется как некоторая функция от численных значений совокупности цифр, представляющих это число. Цифры в непозиционных системах счисления соответствуют некоторым фиксированным числам. Пример непозиционной системы - римская система счисления. В вычислительной технике непозиционные системы не применяются.

Систему счисления называют позиционной, если одна и та же цифра может принимать различные численные значения в зависимости от номера разряда этой цифры в совокупности цифр, представляющих заданное число. Пример такой системы - арабская десятичная система счисления.

В позиционной системе счисления любое число записывается в виде последовательности цифр:

A = + a_m-1 a_m-2... a_k... a₀, a_-1... a_-l (I)

— символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

*даёт представления множества чисел (целых и/или вещественных);

*даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);

*отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на позиционные, непозиционные и с мешанные.

*В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.

*В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

*Цифры - система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т. н. «арабские цифры»). Сочетания этих цифр порождают дву-(и более) значные коды и числа.

 

16. Правило перевода: 1)числа из q-ичной СС в десятичную; 2)целого числа из 10-ной в q-ичную; 3)десятичные дроби в q-ичную; 4)нецелого числа из 10 в q-ичную. Арифметика двоичной системы счисления.

 

17. Основы машиной арифметики:

Целые числа в ЭВМ могут быть представлены в виде:

прямого кода. Прямой код двоичного числа совпадает по изображению с записью самого числа.

обратного кода. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

дополнительного кода. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.

 

18.Формы представления чисел в ЭВМ. В вычислительных машинах применяются две формы представления чисел:

*естественная форма или форма с фиксированной запятой (точкой);

*нормальная форма или форма с плавающей запятой (точкой);

Естественная форма

В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.

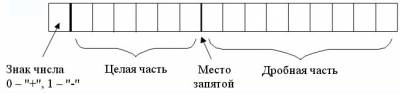
Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.

A = [A] · K^А,

где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, K^А - масштабный коэффициент.

Естественная форма числа в неявном, условном виде реализуется формулой:

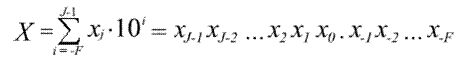
т.е. число записывается только с помощью набора значащих цифр x_j без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

Нормальная форма

С плавающей запятой (ПЛЗ) числа изображаются в виде:

X = ± M×P ^±r,

где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×10², 0,36×10^-2, –0,1082×10³.

Нормализованная экспоненциальная запись числа - это запись вида a= m*P^q, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом m - мантиссa числа, q - порядк числа.

Tо есть нормальная форма реализуется формулой: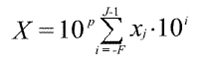

Нормальная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

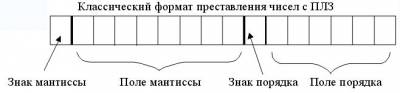
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, используется так называемый смещённый порядок, который рассчитывается по формуле 2^(a-1) + ИП, где a - количество разрядов, отводимых под порядок, ИП - истинный порядок.

В конкретной ЭВМ диапазон представления чисел с плавающей запятой зависит от основания системы и числа разрядов для представления порядка. При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Точность вычислений при использовании формата с плавающей запятой определяется числом разрядов мантиссы. Она увеличивается с увеличением числа разрядов.

Алгоритм представления числа с плавающей запятой:

перевести число из p-ичной системы счисления в двоичную;

представить двоичное число в нормализованной экспоненциальной форме;

рассчитать смещённый порядок числа;

разместить знак, порядок и мантиссу в соответствующие разряды сетки.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена информацией, экономии памяти и удобства операций над десятичными числами предусматриваются специальные форматы их представления: зонный (распакованный) и упакованный. Зонный формат используется в операциях ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.