ОТЧЕТ ПО ЛАБАРАТОРНОЙ РАБОТЕ
«Изучение закона динамики вращательного движения с помощью маятника Обербега»
Вариант №7
| Выполнила: Л. А. Мурадова Студент 1 курса группы М-153 Выполнил: Л. А. Мурадова «18» ноябрь 2013г. Принял: Т. Ю. Васинькина «» 2013г. Работа защищена с оценкой __________________________ «__» ____________ 2013 г. Т. Ю. Васинькина |
Работа №3. Изучение закона динамики вращательного движения с помощью маятника Обербега
ЦЕЛЬ: Получить экспериментальную зависимость углового ускорения от момента силы и определить момент инерции маятника динамическим методом.
ОБОРУДОВАНИЕ: Маятник Обербека, секундомер, штангенциркуль, линейка, набор грузов, весы.
ОПИСАНИЕ УСТАНОВКИ
Основная часть установки – крестообразный маятник, который может вращаться с малым трением вокруг оси О.
По стержням крестовины могут перемещаться подвижные цилиндры (3) массой m0 = 144 г. На одной оси с крестовиной насажены шкивы (1) и (2) разного радиуса r (r 1 = 18 мм, r 2 = 10 мм). К концу нити, намотанной на один из шкивов и перекинутой через невесомый блок (4), прикрепляют груз массой m, приводящий маятник во вращательное движение. Время прохождения грузом расстояния h измеряют секундомером. Маятник в исходном положении удерживается электромагнитом, при нажатии клавиши «пуск» секундомера электромагнит отключается, груз начинает двигаться и одновременно включается секундомер. Счет времени заканчивается при достижении грузом нижнего положения. Для того, чтобы секундомер сработал, необходимо установке с помощью винтов в основании платформы придать такое положение, при котором груз опускался бы точно в отмеченный круг. В этот круг вмонтирован датчик, выключающий секундомер.
Расстояние h отмечается по линейке, установленной в верхней части установки, на которой указывается расстояние груза в начальном положении от основания установки.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
Приняв, что нить невесома и нерастяжима, можно считать движение грузов равноускоренным. Ускорение груза a определяют, измерив время его движения t и пройденный путь h:
.
Угловое ускорение маятника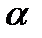 
выразим через линейное ускорение и радиус шкива r:
.
Силу натяжения нити Т можно определить, применив к движению груза массой m закон Ньютона (пренебрегая при этом сопротивлением воздуха):
,
так как обычно 
.
Таким образом, измерив для груза массой m время t прохождения им расстояния h, можно рассчитать угловое ускорение а маятника и определить момент силы, действующий на маятник:
.
При вращении маятника на него действует также тормозящий момент сил трения Mтр, и поэтому закон динамики принимает вид:
.
Это уравнение позволяет найти момент инерции блока I динамическим методом, измерив ряд величин а и М. Для более точного определения величины I в опыте получают зависимость 
, линейный характер которой позволяет рассчитать среднее значение I по угловому коэффициенту опытной прямой.
ОПЫТНЫЕ ДАННЫЕ
Задание 1. Изучение закона вращения маятника.
Таблица 1
| h = м | |||||
| r, мм | № | m, г | t, с | M, Н  м
| α, с-2 |
| r1 = 10 | 90,1 | 22,7 | 8,83*10-3 | 0,214 | |
| 146,2 | 18,1 | 14,33*10-3 | 0,34 | ||
| 192,6 | 18,88*10-3 | 0,56 | |||
| 248,7 | 12,3 | 24,37*10-3 | 0,73 | ||
| r2 = 17,5 | 90,1 | 12,7 | 16*10-3 | 0,39 | |
| 146,2 | 10,1 | 25,1*10-3 | 0,62 | ||
| 192,6 | 33*10-3 | 0,78 | |||
| 248,7 | 7,6 | 42,7*10-3 | 1,09 | ||
| Координаты средней точки | 22,9*10-3 | 0,6 |
РАСЧЕТЫ
| 
|
|
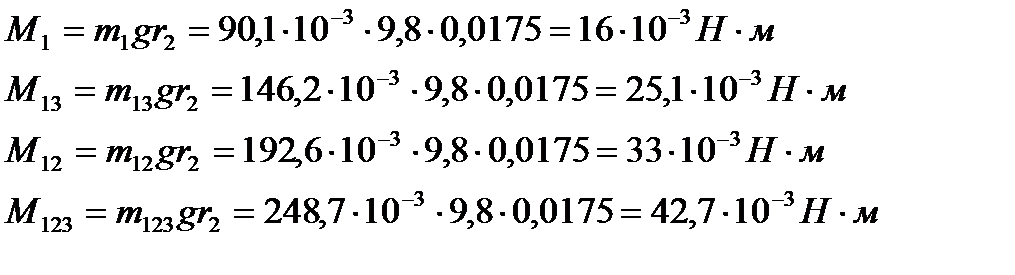
∆α=0,11
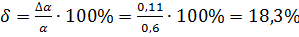
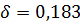
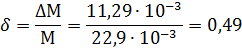
Задание 2. Измерение динамическим методом момента инерции крестовины маятника.
Таблица 2
| h =0,55 м, m =248,7*10-3 кг, r=175 мм | ||||
| № | l, см | t, с | l2, см2 | I, кг м2
|
| 26,4 | 10,5 | 696,96 | 77,57*10-3 | |
| 24,4 | 10,3 | 595,36 | 71,68*10-3 | |
| 22,4 | 10,1 | 501,76 | 68,92*10-3 | |
| 20,4 | 9,7 | 416,16 | 63,57*10-3 | |
| 18,4 | 9,1 | 338,56 | 55,94*10-3 | |
| 16,4 | 8,6 | 268,96 | 49,95*10-3 | |
| 14,4 | 8,1 | 207,36 | 44,3*10-3 | |
| Lср= 20,4 | tср = 9,5 | Lср 2 = 432,16 | Iср =61,7*10-3 |
РАСЧЕТЫ
Вывод
Полученная масса грузов примерно равна массе, указанной на стенде. Относительная погрешность измерений составила:
=0,49
Следовательно, измерения были достаточно точными.
Доверительная вероятность:
0,98
Учитывая полученную величину относительной погрешности, можно утверждать, что точность измерений в ходе работы была достаточной.
Ответы на контрольные вопросы
1. Закон динамики вращательного движения: 
2. Равноускоренное вращение - это движение тела по окружности с постоянным угловым и линейным ускорением. Чтобы тело совершало равноускоренное вращательное движение, необходимо наличие силы, действующей на тело по касательной к траектории движения.
3. Вектор момента силы 
, приводящий маятник во вращение, направлен так же как и сама сила – в плоскости траектории движения по касательной.
Вектор углового ускорения 
сонаправлен с вектором угловой и линейной скорости, а также с вектором линейного ускорения, который, в свою очередь сонаправлен с вектором силы. Таким образом, вектор углового ускорения направлен по касательной в плоскости траектории движения.
Момент импульса тела 
сонаправлен с импульсом, а следовательно и с силой.
Таким образом, все вышеперечисленные векторы – 
и направлены по касательной к траектории движения.
4. а) Угловая скорость зависит от массы грузов.
б) Момент инерции маятника зависит от расстояния цилиндров маятника от оси вращения.
в) Момент силы, действующий на маятник, зависит от момента инерции и углового ускорения – 
которые в свою очередь зависят от массы грузов и от расстояния, на котором расположены цилиндр маятника от оси вращения.
5. В основе динамического метода измерения момента инерции лежит прямая пропорциональная (линейная) зависимость.
6. Величины, определяющие наклон прямой на указанном графике – масса груза и время.
7. В данной работе изменяют момент силы путем изменения массы грузов, либо путем изменения радиуса шкива, либо изменением расстояния цилиндров маятника от оси вращения.
8. Для определения величины углового ускорения в данной работе измеряют время движения, расстояние, которое проходит груз (высоту), а также радиус шкива.
Для определения величины момента силы в данной работе измеряют массу груза и радиус шкива.
9. В данной работе для изменения момента инерции маятника можно изменять расстояние, на котором расположены цилиндры от оси вращения.
