Лабораторная работа №1
Исследование характеристик реактивных двухполюсников.
Цель работы: изучение свойств различных реактивных двухполюсников по данным измерений их основных характеристик.
Измерение модуля и угла сопротивления двухполюсника.
Для измерения модуля и угла сопротивления двухполюсника применяется схема:
Измерение модуля и угла сопротивления двухполюсника Z дв производится при помощи неуравновешенного дифференциального моста. При измерениях таким мостом в качестве эталонного сопротивления, включаемся в одно из плеч моста, используя лишь один магазин сопротивления Rм.
Для измерения модуля сопротивления двухполюсника включаем в схему генератор и подаем от него сигнал. За тем изменяя сопротивления магазинов сопротивления добиваемся равенства напряжений на сопротивлении Rм и Z дв.
При равенстве этих напряжений получаем Rм = Z дв, т.е.модуль измеряемого двухполюсника будет равен сопротивлению магазина сопротивлений. При этом условии однако мост не уравновешен: между точками 1 и 4 его схемы будет напряжение, зависящее от угла сопротивления двухполюсника φдв. Сравнивая это неуравновешенное напряжение с напряжением на одном из плеч моста, можно определить угол φдв.
Угол сопротивления двухполюсника определяется по формуле:
Для L и С
| Частота f,Гц | Напряжение на полуобмотке дифференциального трансформатора,U 3-4,В | Напряжение в диагонали моста,U1-4,В | Модуль сопротивления 2-х полюсника |Zдв|,Ом | Угол сопротивления
2-х полюсника,
|
| 0.33 | 0.25 | -1.297 | ||
| 0.58 | 0.39 | -1.325 | ||
| 0.49 | 0.31 | -1.128 | ||
| 0.61 | 0.38 | -1.114 | ||
| 0.55 | 0.27 | -0.913 | ||
| 0.53 | 0.24 | 0.85 | ||
| 0.55 | 0.27 | 0.913 | ||
| 0.60 | 0.35 | 1.056 | ||
| 0.67 | 0.44 | 1.162 | ||
| 0.77 | 0.55 | 1.24 | ||
| 0.72 | 0.52 | 1.251 |
Графики зависимостей величин и от частоты тока
| Частота f,Гц | Катушка индуктивности | ||||
| Модуль сопротивления |XL|,Ом | Напряжения U3-4,В | Напряжения U1-4,В | Угол сопротивления | добротность QL | |
| 0.66 | 0.52 | 1.335 | 1.009 | ||
| 0.58 | 0.48 | 1.383 | 0.998 | ||
| 0.5 | 0.47 | 1.509 | 0.996 | ||
| 0.56 | 0.55 | 1.553 | 0.998 | ||
| 0.57 | 0.56 | 1.553 | 0.998 | ||
| 0.4 | 0.41 | 1.595 | 1.009 | ||
| 0.42 | 0.49 | 1.724 | 1.026 |
| Частота f,Гц | Конденсатор | ||||
Модуль сопротивления  ,Ом
| Напряжения U3-4,В | Напряжения U1-4,В | Угол сопротивления
| добротность Qс | |
| 0.53 | 0.54 | 1.589 | 0.928 | ||
| 0.48 | 0.47 | 1.55 | 0.945 | ||
| 0.39 | 0.38 | 1.545 | 0.986 | ||
| 0.51 | 0.5 | 1.551 | 0.999 | ||
| 0.5 | 0.49 | 1.551 | 0.999 | ||
| 0.55 | 0.56 | 1.589 | 1.011 | ||
| 0.36 | 0.39 | 1.651 | 1.045 |
Кривые зависимостей величин , 
, от частоты тока в катушке индуктивности.
Кривые зависимостей величин,, от частоты тока в конденсаторе.
2. Определение добротности двухполюсников.
Добротность реактивного элемента определяется по формуле:
где ω – частота тока
Добротность резонансного контура определяется по формуле:
,
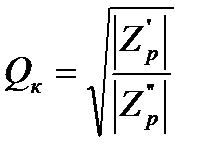где 
и 
– соответственно модули сопротивлений параллельного и последовательного контуров на резонансной частоте.
Кривые зависимостей величин и,от частоты тока в катушке индуктивности и конденсаторе.
Измерение резонансной характеристики и определение полосы частот пропускания контура.
Схема для определения резонансной характеристики параллельного контура.
| f | |||||||||||
| U | 0.07 | 0.085 | 0.1 | 0.14 | 0.22 | 0.3 | 0.26 | 0.19 | 0.13 | 0.1 | 0.08 |
Кривя зависимости напряжения Uк. от частоты тока, полоса пропускания.
0.707-const-корень из общей (P) мощности
Вывод: Для определения ширины полосы пропускания частот контура, необходимо найти на кривой точки, соответствующие отметкам на оси напряжений Um/ 
, где Uрк – напряжение на контуре при резонансной частоте. Полоса частот Δf, заключенная между этими точками и будет полосой пропускания частот контура. Δf= 695-670 =25
Добротность контура определим по формуле: Qk=fp/ Δf, где fр – резонансная частота контура. Qk=695/25=27,8. Чем Δf уже, тем добротность больше.
Лабораторная работа №2
