Принцип оптимальности: каково бы ни было состояние S системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.
Уравнения Беллмана. На каждом шаге любого состояния системы Sk-1 решение Хk нужно выбирать "с оглядкой", так как этот выбор влияет на последующее состояние Sk и дальнейший процесс управления, зависящий от Sk. Но есть один шаг, последний, который можно для любого состояния Sn-1 планировать локально-оптимально, исходя только из
соображений этого шага. Zn = fn(Sn-1; Xn) Согласно принципу оптимальности Хn нужно выбирать так, чтобы для любых состояний Sn-1 получить максимум целевой функции на этом шаге. Zn*(Sn-1) = opt fn(Sn-1; Xn) - называется условным оптимумом (max, min) целевой функции на n-м шаге.
Решение Хn при котором достигается Zn* также зависит от Sn-1 и называется условным оптимальным управлением на n-м шаге. Решив одномерную задачу локальной оптимизации по уравнению Zn*(Sn-1) = opt fn(Sn-1; Xn) найдем для всех возможных состояний Sn-1 две функции: Zn*(Sn-1) и Xn*(Sn-1).
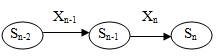Рассмотрим теперь двухшаговую задачу: присоединим к n-му шагу (n-1)-й: fn-1(Sn-2; Xn-1),
fn-1(Sn-2; Xn-1)+Zn*(Sn-1) – значение целевой функции на 2-х последних шагах.
Согласно принципу оптимальности для любых Sn-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения по всем допустимым управлениям Xn-1.
Z*n-1(Sn-2) = opt (fn-1 (Sn-2; Xn-1)+Zn*(Sn-1)). Z*(n-2) – условный max (min) целевой функции при оптимальном управлении на 2-х последних шагах. Управление, соответствующее этому значению целевой функции обозначается X*n-1(Sn-2) и называется условным оптимальным управлением на n-1 – шаге.
Sn-1 = φ n-1 (Sn-2; Sn-1), Z*n-1(Sn-2), т.к. состояние Sn-1 можно выразить через состояние Sn-2, то Z зависит только от Sn-2.
Z*k(Sk-1) = opt (fk(Sk-1;Xk) + Z*k+1(Sk)) – уравнение Беллмана, k=n-1, n-2, n-3 (изменяется в сторону уменьшения).
Постановка и решение задачи о распределении ресурсов между предприятиями.
Постановка и решение задачи о ремонте и замене оборудования.
Постановка и решение задачи о выборе оптимального маршрута.
V. Задачи Теории игр
