Анализ чувствительности
В соответствии с рис.1 два ресурса – Материал 1 и Материал 2 – расходуются полностью. Эти ограничения называются лимитирующими. Однако для обоих типов изделий остается неиспользованной часть производственных мощностей.
Определим предел лимитирующих и нелимитирующих ресурсов, для этого представим систему ограничений в виде уравнений. Для этого в каждое ограничение введем дополнительную переменную для преобразования неравенств в уравнения.
При этом должно соблюдаться условие не отрицательности:
х 3… х 6 ≥ 0
х 1 + х 3 = 11 (1)
х 2 + х 4 = 8 (2)
10 х 1 + 15 х 2 + х 5 = 150 (3)
20 х 1 + 12 х 2 + х 6 = 240 (4)
Подставим координаты точки D (10;3,33).
1) для (1)-го ресурса х 3 = 11-10 = 1 шт.
Ресурс (1) не лимитирующий. Имеются лишние площади и оборудование, позволяющее выпускать 1 шт. продукции А.
2) для (2)-го ресурса
3,33 + х 4=8 ⇒ х 4=4,67 шт.
Ресурс (2) не лимитирующий. Имеются лишние площади и оборудование, позволяющее выпускать 4,67 шт. продукции В.
3) для (3)-го ресурса
х 5=150-10*10-15*3,33=0
Ресурс (3) – Материал 1 расходуется полностью и является лимитирующим.
4) для (4)-го ресурса
х 6=240-20*10-12*3,33=0
Ресурс (4) – Материал 2 расходуется полностью и является лимитирующим.
II. Исследование возможности увеличения лимитирующих ресурсов.
Поскольку два ресурса используются полностью, то значение целевой функции ограничено.
1) Пусть есть возможность увеличения ресурса (3).
Так как жесткость лимитирующего ограничения постепенно снижается, его график будет перемещаться параллельно своему начальному положению в сторону противоположную от начала координат, одновременно будет происходить перемещение оптимальной крайней точки в направлении, которое улучшает значение целевой функции. Снижение жесткости на Материал1 является эффективным до тех пор, пока линия ограничения не достигнет точки пересечения ограничений на производственную мощность на производство изделия В и линии ограничения на Материал2. Получили точку D′.
Найдем координаты точки D'.
В точке D' пересекаются линии (2) и (4). Решаем систему уравнений, х 2=8 20 х 1+12 х 2=240 20 х 1+96=240 ⇒ х 1=7,2 D' (7,2; 8) Подставляем координаты в целевую функцию:
15*7,2+12*8=204 у.е. в неделю.
Таким образом, увеличение дохода в неделю составит:
= 204-189,96 = 14,04 у.е.
Количество Материала 1, используемое для производства данного ассортимента равно:
10*7,2 + 15*8 = 192 кг Оно превышает начальное количество (192 кг -150 кг) на 42 кг в неделю. В новой оптимальной точке производственная мощность для продукции В используется максимально. Дополнительное количество Материала1 – 42 кг – позволяет получать дополнительный доход, равный 14,04 у.е. следовательно теневая цена данного ресурса составит:
у.е. за килограмм. Каждый дополнительный килограмм Материала1 ведет к увеличению еженедельного дохода 0,33 у.е. Из этого следует, что сверхнормативный запас этого ресурса целесообразен только в случае, если дополнительная стоимость получения любого дополнительного количества ресурса не превышает 0,33 у.е. за 1 кг Материала1. 2) Предположим, что ограничение на Материал1 остается неизменным, применим аналогичную процедуру к Материалу2, т.е. пусть есть возможность увеличения ресурса (4).
Так как жесткость лимитирующего ограничения постепенно снижается, его график будет перемещаться параллельно своему начальному положению в сторону противоположную от начала координат, одновременно будет происходить перемещение оптимальной крайней точки Е в направлении, которое улучшает значение целевой функции. Снижение жесткости на Материал2 является эффективным до тех пор, пока линия ограничения не достигнет точки пересечения ограничений на производственную мощность на производство изделия А и линии ограничения на Материал1. Получили точку Е′.
Найдем координаты точки Е'.
В точке Е' пересекаются линии (1) и (3). Решаем систему уравнений, х 1=11 10 х 1+15 х 2=150 110+15 х 2=150 ⇒ х 2=2,7 Е' (11; 2,7) Подставляем координаты в целевую функцию:
15*11+12*2,7= 197,4 у.е. в неделю
Таким образом, увеличение дохода в неделю составит:
= 197,4-184,92 = 12,48 у.е.
Количество Материала 2, используемое для производства данного ассортимента равно:
R Е′ = 20*11 + 12*2,7 = 252,4 кг Оно превышает начальное количество (252,4 кг - 240 кг) на 12,4 кг в неделю. В новой оптимальной точке производственная мощность для продукции А используется максимально. Дополнительное количество Материала2 – 12,4 кг – позволяет получать дополнительный доход, равный 12,48 у.е. следовательно теневая цена данного ресурса составит:
у.е. за килограмм. Каждый дополнительный килограмм Материала2 ведет к увеличению еженедельного дохода на 1,01 у.е. Из этого следует, что сверхнормативный запас этого ресурса целесообразен только в случае, если дополнительная стоимость получения любого дополнительного количества ресурса не превышает 1,01 у.е. за 1 кг Материала2.
III. Исследование возможности изменения коэффициентов целевой функции.
Рассмотрим изменение коэффициентов целевой функции. Т.к. коэффициенты целевой функции определяют прибыль и изменение стоимости сырья приведет к изменению значений коэффициентов целевой функции, то необходимо определить, каков промежуток значений единичного дохода, для которых Д остается оптимальной точкой.
Построим условную функцию q, проходящую через точку Д.
При 
, 
Получили координаты первой точки (0; 15,8)
Вторую точку можно не находить, т.к. целевая функция проходит через точку Д.
Обозначим а доход от единицы продукции А и б доход от единицы продукции В.
1) Запишем выражение целевой функции в виде:
Выразим отсюда х 2
(*) Ограничениями для целевой функции являются линии: нижняя (3) и верхняя (4).
Начинаем вращать целевую функцию вокруг точки Д и совместим ее с линией (3)
10 х 1+15 х 2=150
Рассчитаем нижнее ограничение:
⇒ a = 8
Совместим q с линией (4) и найдем верхнее ограничение.
20 х 1+12 х 2 = 240
⇒ a = 20
Следовательно, определился предел изменения коэффициентов:
8 ≤ а ≤ 20
2) Определим при каком изменении коэффициента б сохраняется максимальное значение целевой функции.
Выразим отсюда х 1
Ограничениями для целевой функции являются линии: нижняя (4) и верхняя (3).
Начинаем вращать целевую функцию вокруг точки Д и совместим ее с линией (4)
20 х 1+12 х 2=240
Рассчитаем нижнее ограничение:
⇒ б = 9
Совместим q с линией (3) и найдем верхнее ограничение.
10 х 1+15 х 2 = 150
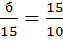⇒ б = 22,5
Следовательно, определился предел изменения коэффициентов для продукта В:
9 ≤ а ≤ 22,5
