Принцип управления по возмущению

Основные принципы регулирования. Регулирование по разомкнутому циклу. Регулирование по возмущению. Регулирование по отклонению (по ошибке). Обратная связь.

В основе построения системы автоматического управления лежат некоторые общие фундаментальные принципы управления, определяющие, каким образом осуществляется увязка алгоритмов функционирования и управления с фактическим функционированием или причинами, вызывающими отклоне­ние функционирования от заданного. В настоящее время в тех­нике известны и используют три фундаментальных принципа: разомкнутого управления, компенсации и обратной связи.

Принцип разомкнутого управления

используется на вспомогат. операц. (закрыт - открыт)

Работу систем автоматического управления можно описывать с помощью функциональных схем, которые показывают из каких элементов состоит система и как эти элементы связаны между собой.

Под функциональным элементом понимается конструктивно обособленная часть системы выполняющая определенные функции: измерения, усиления, сравнения, преобразования.

Недостаток: невысокая точность системы управления — отсутствие информации о действительном значении управляемой величины.

Принцип управления по возмущению.

Идея принципа: необходимо каким-либо образом измерить возмущающее воздействие и в зависимости от результатов измерения оказать на объект управления управляющее воздействие, устанавливающее вредное влияние измеренного возмущения.

Недостатки принципа:

- инвариантность управляемой величины обеспечивается лишь по отношению к тому возмущению, которое измеряется.

- инвариантность управляемой величины достигается лишь при строгом соответствии параметров элементов системы расчетным образом.

3. Принцип обратной связи:

ОУ — объект управления; ИП — измерительный преобразователь

ЗУ — задающее устройство; ЭС — элемент сравнения

У — усилитель устройства; ИУ — исполнительное устройство

РО — регулирующий орган

y(t) — управляемая, регулируемая величина.; g(t) — задающее воздействие

E(t) — ошибка регулирования; f(t) — внешнее воздействие

 

Принципы управления. Выделяют три фундаментальных принципа создания систем управления: разомкнутое управление, компенсирующее управление и управление с обратной свя- зью (замкнутое управление).

При разомкнутом управлении программа управления жестко задана в УУ и влияние возму- щений на параметры процессов не учитывается. Примерами таких систем являются часы, магни- тофон, компьютер, и т.п. Разомкнутое регулирование применяется при наличии двух условий:

- достаточной информации о свойствах объекта и их постоянстве в процессе работы;

- незначительном уровне помех или их полном отсутствии.

В простых разомкнутых системах (рис. 1.3.1) управляющее воздействие u(t) формируется управляющим устройством как функция задающе- го или возмущающего воздействия. Если известна модель объекта у = G(u, x) в алгебраической или дифференциальной форме и известна необходимая реакция у(t), то решается обратная задача u(t) =

Y(у(t), x(t)) и определяется управление, которое необходимо для реализации реакции объекта 2. Найденный закон управления u(t) реализуется регулятором 1. Однако такое управление можно реализовать в том случае, если x(t) = const.

Для уменьшения или устранения отклонения управляемой величины от требуемого значе- ния, вызываемого влиянием того или иного фактора, необходимо, чтобы управляющее воздействие было определенной функцией этого фактора и характеристик объекта.

На рис. 1.3.2 представлена структура, реа- лизующая принцип управления по возмущению, которая применяется при x(t) = var, но величина x(t) поддается измерению и ее значение может по- даваться на вход управляющего устройства, обес- печивая соответствующую реакцию воздействия u(t) на изменения значения x(t).

Принцип управления по возмущению состоит в том, что для уменьшения или устранения отклонения y(t) управляемой величины от требуемого значения, вызываемого возмущающим воз- действием x(t), измеряется это воздействие и в результате его преобразования вырабатывается управляющее воздействие u(t), которое, будучи приложено к входу объекта управления 2, вызывает компенсирующее отклонение управляемой величины противоположного знака по сравнению с от- клонением y(t).

Основной недостаток разомкнутых систем - практическая невозможность иметь идеально

точную модель системы у = G(u, x) с учетом всех действующих возмущений, равно как и измерять все регулярные и нерегулярные возмущения. Разомкнутые системы обычно не применяются для управления неустойчивыми объектами и объектами с изменяющимися параметрами.

Если воздействие возмущающих факторов может искажать выходную величину системы до недопустимых пределов, то применяют принцип компенсации с использованием корректирую- щего устройства. Для задания параметров коррекции должно проводиться изучение соответст-

вующего возмущающего фактора или создаваться его математическая модель. Примеры систем компенсации: биметаллический маятник в часах, компенсационная обмотка машины постоянного тока и т.п. Принцип компенсации обеспечивает быструю реакции на возмущения и более высокую эффективность управления, но, как правило, используется для компенсации только определенных дестабилизирующих факторов и не может защитить от всех возможных возмущений.

Наибольшее распространение в технике получило управление с обратной связью, при ко- тором управляющее воздействие корректируется в зависимости от выходной величины y(t). Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Для выполнения данной операции выход ОУ соединяется с вхо- дом устройства управления главной обратной связью (ОС). Это самый дорогой вид управления, при этом канал обратной связи является наиболее уязвимым местом системы. При нарушении его работы система может стать неустойчивой или полностью неработоспособной.

 

 

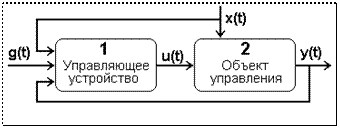
Структура замкнутых систем управления представлена на рис. 1.3.3. Управляющее воздействие u(t) формируется как функция рассогласо- вания (t) = g(t) - y(t) текущего значения управ- ляемой переменной от требуемого задающего воздействия. Эта фундаментальная идея лежит в основе принципа управления по отклонению, ко-

торый реализуется замкнутыми системами. Принцип управления по отклонению универсален, т. к. позволяет достигать цели управления независимо от причин рассогласования - изменения внут- ренних свойств объекта и внешних воздействий.

Замкнутые системы позволяют решать все задачи управления: стабилизации, слежения и программного управления. Неустойчивые объ- екты могут быть управляемы только системами с замкнутыми структурами. Обобщением рас- смотренных принципов управления является принцип комбинированного управления (рис. 1.3.4), который позволяет в замкнутой системе

использовать и принцип управления по возмущению.

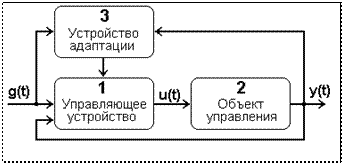Системы, способные изменять закон управления с целью осуществления наилучшего в некотором смысле качества управления неза- висимо от внешних воздействий (рис. 1.3.5), ис- пользуют принцип адаптации. Показатель каче- ства обрабатывается устройством адаптации 3 для изменения структуры управляющего уст- ройства или его параметров.

Отметим, что при введении обратной связи система управления становится инерци-

онной. Поэтому часто применяют комбинацию обратной связи с принципом компенсации, что по- зволяет объединить достоинства обоих принципов: быстроту реакции на возмущение при компен- сации и точность регулирования независимо от природы возмущений от обратной связи.

 

43) Раскройте управляемость в линейных системах управления.

Управляемость и наблюдаемость относятся к основным понятиям теории автоматического регулирования, которые позволяют оценить структуру системы на этапе анализа.

Если в системе управления формируется управляющее воздействие размерности , превышающее число степени свободы объекта, описанного уравнением

,

то система является неуправляемой. В такой системе нельзя перевести объект из начального состояния в любое конечное состояние под действием некоторого управляющего воздействия. Таким образом, систему называют полностью управляемой, если ее можно перевести в конечное состояние в течение фиксированного интервала времени.

 

 

Необходимое и достаточное условие полной управляемости для линейной стационарной системы, представленной уравнением:

,

где -мерный вектор; -матрица; -матрица; -мерный вектор,заключается в том, чтобы матрица управляемости

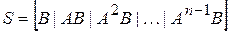
должна иметь ранг .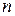

С понятием управляемости связано понятие наблюдаемости, которое позволяет установить начальное состояние системы по результатам измерений одного выходного сигнала.

Необходимое и достаточное условие полной наблюдаемости для линейной стационарной системы, представленной уравнениями:

,

,

где – n -мерный вектор, -матрица, -матрица, -мерный вектор, -мерный вектор, -матрица, -мерная матрица,заключается в том, что матрица наблюдаемости

 

должна иметь ранг .

Матрицы и являются сопряженными матрицами по отношению к матрицам и . При действительных значениях элементов 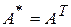и . При комплексных числах матрицы и равны соответствующим комплексно-сопряженным.

Для линейных стационарных систем матрица наблюдаемости записывается:

или

.

При выполнении условия наблюдаемости возможно определение начального состояния по следующим данным:

а) по матрицам 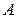и ;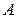

б) по выходному сигналу от начальных условий при , заданному на конечном интервале времени 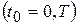, где Т – интервал функционирования системы регулирования.

Рассмотрим два типа систем автоматического регулирования.

Первый тип. Система имеет только один выходной сигнал

.

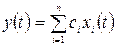Для такой системы необходимым и достаточным условием полной наблюдаемости является отличие от нуля всех коэффициентов .

Второй тип. Система имеет несколько выходных сигналов

, .

Необходимым и достаточным условием полной наблюдаемости является то, что для каждого -го произведения один из коэффициентов не должен равняться нулю.

Практический пример

Определить выполнение условий управляемости и наблюдаемости системы регулирования, представленной следующей структурной схемой (рис. 4).

 

Рис. 4. Структурная схема системы регулирования

Запишем уравнения состояния системы, используя определение передаточной функции. Передаточные функции первого и второго звена записываются в виде:

,

.

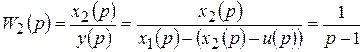Данные уравнения позволяют записать:

После преобразований запишем:

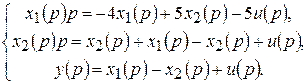
Заменяем и символ «» в скобках переменных на символ «»:

(1)

.

В векторно-матричной форме уравнения (1) имеют вид:

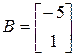, , , (2)

, , . (3)

Матрица имеет размерность и ее ранг равен (т.к. ).

 

44) Какие критерии управляемости Вы знаете?

45) Раскройте наблюдаемость линейных системах управления.

Управляемость и наблюдаемость. Критерии управляемости и наблюдаемости линейных стационарных многомерных объектов При проектировании систем управления сложными многомерными объектами необходимо предварительно оценить такие структурные свойства объектов, как управляемость и наблюдаемость. Математическое описание объекта управления представим в параметрах состояния [3]: , (81) , (82) где X(t) - вектор параметров состояния, X(t) = {X1(t), X2(t),..., Xn(t)}; U(t) - вектор управляющих воздействий, U(t) = {U1(t), U2(t),..., Ur(t)}; Y(t) - вектор выходных переменных, Y(t) = {Y1(t), Y2(t),...,Y l (t)}; А, В, С - матрицы постоянных коэффициентов с размерами соответственно n x n, n x r, l x n. Объект (81) называют полностью управляемым, если его можно с помощью некоторого ограниченного управляющего воздействия U(t) перевести в течение конечного интервала времени tк из любого начального состояния X(0) в заданное конечное состояние X(tк). Для осуществления такого перевода объекта необходимо, но не достаточно, чтобы каждая из переменных состояния Xi (i=1,...,n) зависела хотя бы от одной из составляющих Uj (j=1,...,r) вектора управлений U(t). Без доказательства приведём критерий управляемости линейных стационарных объектов. Пусть матрицы А и В постоянны. Введём так называемую матрицу управляемости , (83) которая состоит из столбцов матрицы В и произведений матриц , ,..., и имеет размерность (n * nr). Справедлив следующий критерий управляемости: линейный стационарный объект X вполне управляем тогда и только тогда, когда ранг матрицы управляемости (83) равен размерности n пространства состояний объекта, то есть если . (84) Запись в правой части (83) означает матрицу, у которой первые r столбцов совпадают со столбцами матрицы В, следующие r столбцов со столбцами произведения матриц АВ и т.д., а последние r столбцов образованы столбцами произведения матриц . Ранг матрицы находят как наибольший порядок отличных от нуля квадратных миноров матриц. Необходимое и достаточное условие (84) означает, что матрица управляемости (83) должна содержать n линейно независимых столбцов. В частном случае, когда ранг матрицы В больше единицы, например равен , условие управляемости имеет вид: . (85) Если управление U(t) - скалярная функция времени и матрица В превращается в матрицу-столбец, то для полной управляемости необходимо и достаточно, чтобы квадратная матрица управляемости Qy не была вырожденной, то есть чтобы её определитель det Qy ¹ 0. В другом частном случае, когда А - диагональная матрица и все её элементы различны, для управляемости необходимо и достаточно, чтобы матрица В не содержала нулевых строк. Если ранг матрицы Qy меньше n, то система будет не полностью управляемой. Наряду с управляемостью состояния X(t) можно рассматривать управляемость выхода Y(t) объекта [3]. Условие управляемости выхода объекта , (86) где - размерность вектора выхода Y(t).