Пример №5
¾ В ходе изучения термического разложения динитроксида на золоте при 990оС получены следующие кинетические данные:
время, мин 30 53 100
степень превращения, % 32 50 73
Определить порядок реакции n и константу скорости k с помощью вычислительной машины. Для решения задачи надо подготовить четыре вычислительных блока: блок, моделирующий собственно химическую реакцию, блок, воспроизводящий экспериментальную кривую,
В уравнении (Т) производим замену: С = С0(1-x), где С0 – начальная концентрация. Получаем: 
(Т*). Для вычисления степени превращения x необходим дополнительный сумматор: - (-x = (1-x) – 1). (константа скорости реакции должна получиться 2.1×10-4 с-1.
Задание аналогично предыдущему, подробно не рассматривается, имеются код программы и различные этапы ее выполнения.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls,Math, ExtCtrls, TeeProcs, TeEngine, Chart, Series;
type
TForm1 = class(TForm)
Memo1: TMemo;
Chart1: TChart;
Edit1: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Button1: TButton;
Button2: TButton;
Button3: TButton;
Chart2: TChart;
Edit2: TEdit;
Label6: TLabel;
Series2: TFastLineSeries;
Edit3: TEdit;
Label7: TLabel;
Edit4: TEdit;
Label8: TLabel;
Memo2: TMemo;
Series4: TFastLineSeries;
Memo3: TMemo;
Memo4: TMemo;
Series3: TLineSeries;
Series1: TLineSeries;
procedureFormCreate(Sender: TObject); {вывод на экран экперимен-тальных данных и построение полулогарифмической зависимости}
procedure Button2Click(Sender: TObject); {очисткатекстовыхполей}
procedure Button3Click(Sender: TObject); {очисткаграфиков}
procedure Button1Click(Sender: TObject); {основнаяпрограмма}
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
i:integer;
tt,al:array [0..3] of real;
k,dt,t,c,n:real;
implementation
{$R *.dfm}
procedure TForm1.FormCreate(Sender: TObject);
begin
tt[0]:=0; al[0]:=0;
tt[1]:=30; al[1]:=0.32;
tt[2]:=53; al[2]:=0.5;
tt[3]:=100; al[3]:=0.73;
memo1.Clear;
memo2.Clear;
memo3.Clear;
memo4.Clear;
for i:=0 to 3 do begin
memo1.Lines[0]:=memo1.Lines[0]+' '+floattostr(tt[i]);
memo2.Lines[0]:=memo2.Lines[0]+' '+floattostr(al[i]);
series1.AddXY(tt[i],1-al[i],'');
series2.AddXY(tt[i],Ln(1-al[i]),'')
end;
k:= abs(ln(1-al[3])-ln(1-al[1]))/(tt[3]-tt[1]);
edit2.Text:=floattostr(k);
n:=100*(ln(al[3])-ln(al[1]))/((ln((1-al[1])/(1-al[3])))*(tt[3]-tt[1]));
//n:=(ln((1-al[1])/(1-al[3]))+(ln(tt[1]/tt[3])))/(ln((1-al[3])/(1-al[1])));
edit3.Text:=floattostr(n);
memo3.Lines[0]:='зеленая - эксперимент, красная - расчет';
memo4.Lines[0]:='зеленая -Ln(1-al[i]), красная - 1-al[i] ';
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
edit1.Text:='';
edit4.text:='';
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
series3.Clear;
series4.Clear;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
c:=strtofloat(edit1.text);
dt:=strtofloat(edit4.text);
t:=0;
while c>0.001 do begin
series3.AddXY(t,c,'');
t:=t+dt;
c:=c-k*power(c,n)*dt;
end;
c:=strtofloat(edit1.text);
for i:=0 to 3 do
series4.AddXY(tt[i],c*(1-al[i]),'');
end;
end.
Рис. 27 Исходная форма.
Рис. 28 Окно программы с расчетом константы скорости (k) и порядка реакции (n)
Рис. 29 Окно программы, ввод данных с клавиаткры
Рис. 30 Рабочее окно с экспериментальной и теоретической зависимостями.
Рис. 31 Рабочее окно, ввод новых данных
Рис. 32Рабочее окно с экспериментальной и теоретической зависимостями.
Задания для лабораторных работ
Все задания, приведенные в пособии, взяты из книг Луценко В.И., Финякин Л.Н. Математическое моделирование химико-технологических процессов на аналоговых вычислительных машинах. Лабораторный практикум (М., Химия, 1984) [1] и К. Эберт, Х. Эдерер Компьютеры. Применение в химии. Пер. с нем., под ред. Н.С.Зефирова (М., Мир, 1988) [13].
Моделирование гомогенных химических реакций
Стехиометрическое уравнение реакции показывает, в каких соотношениях компоненты участвуют в химической реакции. Это уравнение связывает исходные реагенты и конечные продукты и представляет собой материальный баланс в целом или ее отдельных элементарных стадий.
aA + bB Û cC
cC – aA – bB = 0
где а, b, с – количество молей вещества А, В и С и называются стехиометрическими коэффициентами реакции.
В отличие от стехиометрической схемы механизм химической реакции раскрывает элементарные стадии превращения исходных компонентов в конечные продукты. Скорость химической реакции (u)–есть изменение количества молей компонента (ni), происходящее в единицу времени (dt) в единице объема (dV). Кинетическое уравнение реакции записывается в виде:
ui = 
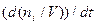
Отношение числа молей i–того компонента к объему реакционной массы V представляет собой концентрацию этого компонента Ci:
Поэтому при постоянном объеме реагентов скорость реакции можно выразить через концентрацию как:
ui 
Для реакции типа aA + bBÛcC скорость при постоянной температуре выражается уравнением uA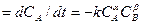 
. Это выражение получают на основании закона действия масс. Здесь a и b определяют порядок реакции. Если стехиометрическое уравнение соответствует механизму реакции (или одной из ее стадий), то ее порядок равен числу молекул, вступивших в реакцию (молекулярность реакции), т.е. a=a, b=b.
Механизм реакции называют истинным, если каждая стадия описывается кинетическим уравнением, составленным в соответствии со стехиометрическим уравнением этой стадии. При этом сумма стехиометрических коэффициентов исходных компонентов равна общему порядку реакции, а порядок реакции по отдельному компоненту равен стехиометрическому коэффициенту этого компонента. В уравнении закона действия масс коэффициент k есть константа скорости химической реакции. Зависимость константы от температуры Т носит нелинейный характер и обычно описывается уравнением Аррениуса:
где k0 – предэкспоненциальный множитель, T – термодинамическая температура, E - энергия активации, R – универсальная газовая постоянная.
Чтобы упростить запись кинетических уравнений, константу скорости реакции рекомендуется относить к одному молю реагента, а соответствующем выражении скорости реакции (или стадии) умножать ее на стехиометрический коэффициент. Таким образом, при выводе уравнения скорости стехиометрию химической реакции следует учитывать не только в величинах порядков, но и в коэффициентах дифференциального уравнения скорости. Например, в реакции H2 + 2NO ® N2O + H2O скорость поглощения NO в два раза выше, чем H2, поэтому система дифференциальных уравнений кинетики имеет вид:
.
Следует подчеркнуть, что для решения системы дифференциальных уравнений с целью получения кинетических кривых для каждого из них необходимо задать начальные условия, т.е. оговорить исходные концентрации соответствующих реагентов. Иногда для формального описания кинетики используют дифференциальные уравнения, подобные приведенным выше, но при этом степени a и b выступают в роли некоторых эмпирических констант и часто принимают дробные значения.
1. Моделирование изотермических реакций, описываемых линейными дифференциальными уравнениями (упражнения).
Задание 1 необходимо получить модели простой необратимой реакции первого порядка, сложной мономолекулярной реакции, протекающей в две последовательные стадии, сложной обратимой реакции первого порядка. Получить кинетические кривые для всех компонентов химических реакций.
¾ получение модели необратимой реакции первого порядка вида А ® В, если известны: начальные концентрации СА(0), кмоль/м3, СВ(0), кмоль/м3, константа скорости химической реакции при температурах Т1 и Т2. Требуется найти для каждой температуры кинетические зависимости компонентов реакции в виде функций СА(t), СВ(t) и время 50%-ного и 80%-ного превращения компенента А.
Для моделирования запишем кинетичекие уравнения для компонента А 
(1) и для компонента В: 
(2). Уравнения (1) и (2) представляют систему линейных уравнений с заданными начальными условиями.
Результаты выводятся в виде таблицы, графиков С(t). Для сравнения времени 50%-ного и 80%-ного превращения компонента А с теоретическим значением применяют выражение: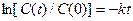 
.
Задание2 моделирование двухстадийной последова-тельной химической реакции вида: А 
В 
С, если известны начальные концентрации СА(0), СВ(0), СС(0), кмоль/м3 и константы скорости k1, k2, с-1. Получить кинетические зависимости компонентов реакции в виде графиков функций С(t), для промежуточного продукта В определить максимально возможный выход, а также момент времени, в который этот максимум достигается. Кинетические уравнения имеют вид: для компонента А - 
; для компонента В -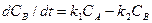 
; для компонента С - 
. Поскольку реакция идет до конца, и вещества А и В полностью превращаются в конечный продукт С, то можно записать следующее: СА max = СА(0) и ССmax = CА(0) + CВ(0) + СС(0). Максимальное значение концентрации продукта В заранее не известно, можно заметить лишь, что СВmax< СА(0) + СВ(0).
По полученной кинетической кривой промежуточного продукта В определяем СВmax и момент времени tBmax, при котором этот максимум достигается. Напоследок целесообразно сравнить получаемое значение СВmax с теоретическим, вычисляемым как СВmax = СА(0)×g1/(1-g), где g = к1/к2 при СВ(0)=0.
Задание 3 Составить кинетическую модель обратимой химической реакции первого порядка вида 
и получить кинетические кривые СА(t) и СВ(t), если известны: начальные концентрациии СА(0) и СВ(0), кмоль/м3 и константы скорости k1 и k2, с-1. Кинетические зависимости компонентов реакции представить в виде графиков функций СА(t) и СВ(t), определить равновесные концентрации и время достижения равновесия при различных соотношениях начальных концентраций и констант скорости прямой и обратной реакций. Кинетические уравнения имеют вид: для компонента А - 
, для компонента В - 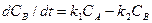. Кроме того, необходимо получить кинетические кривые при различных начальных условиях: СА(0)>СВ(0) для случаев k1<k2, k1=k2, k1>k2; CA(0)=СВ(0) для случаев k1<k2, k1=k2, k1>k2; CA(0)<CB(0) для случаев k1<k2, k1=k2, k1>k2. (В случае, когда СА(0) + СВ(0) = const независимо от начальных условий концентрации стремятся к равновесным значениям, определяемым константой равновесия kp = k1/k2 = CB(¥)/CA(¥).
2. Моделирование изотермических реакций, описываемых нелинейными диференциальными уравнениями.
Задание 4 Составить кинетическую модель необратимой реакции второго порядка вида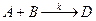 
, если известны: начальные концентрации реагентов СА(0) и СВ(0), кмоль/м3, константа скорости реакции к, м3/(кмоль×с). Получить кинетические зависимости компонентов реакции в виде графиков функций СА(t), CB(t), CD(t); определить время 50%-ного превращения компонента А. Кинетические уравнения имеют вид: для компонента А –
, для компонента В - 
, для компонента D - 
. Искомые кинетические зависимости СА(t), CB(t), CD(t) получаем в виде графиков, по графику СА(t) определяем время 50%-ного превращения компонента А.
Задание 5 Составить кинетическую модель обратимой реакции второго порядка вида: 
, если известны: начальные концентрации компонентов СА(0), СВ(0), СD(0) кмоль/м3; константы скорости реакции к1, к2 м3/(кмоль×с). Получить кинетические зависимости реагентов в виде графиков функций CA(t), CB(t), CD(t) и определить время, в течение которого образуется половина максимального количества продукта D. Кинетические уравнения имеют вид: для компонента А - 
, для компонента В - 
, для компонента D -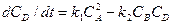 
. Надо учесть, что продукты В и D образуются в эквимолярных количествах и при нулевых начальных концентрациях их концентрации не могут превысить величины, равной половине начальной концентрации исходного компонента А, т.е. (СВ макс. = СD макс.) £ 0.5 СА(0).
Задание 6 Составить модель сложной последовательно-параллельной гомогенно-каталитической реакции второго порядка вида 
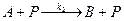. Реакция двухстадийная, каждая стадия протекает по второму порядку. Известны: начальные концентрации CD = 0.2, Cp =0.3 кмоль/м3; константы скорости к1 = 5×10-3, к2 = 2×10-3 м3/(кмоль×с).
Найти кинетические зависимости CD(t), CP(t), CA(t), CB(t).
Задание 7 Получить также кинетические зависимости при условии, что вторая стадия не является каталитической и протекает по первому порядку: 
при к2 = 3×10-4 с-1. Сравнить полученные кривые с соответствующими кривыми из предыдущего варианта. Кинетические уравнения имеют вид: для компонента D - 
, для компонента Р - 
, для компонента А - 
, для компонента В - 
.
Для второго варианта кинетическое уравнение будет иметь вид: для компонента А - , для компонента В -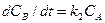 
. При моделировании реакции по второму варианту константу скорости второй стадии следует откорректировать так, чтобы кинетическая кривая компонента В могла быть наложена на соответствующую кривую, получаемую по первому варианту.
3. Моделирование неизотермических реакций.
Получить модель химической реакции, протекающей с тепловым эффектом. Определить зависимость между степенью превращения (концентрацией) исходного компонента и температурой реакционной смеси при двух режимах проведения реакции – адиабатическои и изотермическом.
Задание 8 Составить модель реакции разложения первого порядка типа А ® В + С, протекающей в адиабатическом режиме с тепловым эффектом, если известны: начальные концентрации и температура, тепловой эффект, теплоемкости реагентов, зависимость константы скорости реакции от температуры, приведенная ниже:
Т, оС ……50 55 60 65 70 72.5 78 84
к, ч-1 …1.4 1.6 2.2 3.0 4.0 4.7 7.2 9.4
Получить временные зависимости концентрации исходного компонента, концентраций продуктов реакции и температуры, построить зависимость скорости превращения реагента А от его концентрации в виде функции dCA/dt = -k(T)CA(t). Математическое описание химической реакции с тепловым эффектом включает уравнение материального (кинетические) и теплового балансов. Кинетическое уравнение для исходного компонента реакции: 
. Уравнение теплового баланса при адиабатическом режиме имеет вид: 
, где cV = (cACA + cBCB + cCCC)V. Здесь сV – объёмная теплоемкость системы, зависящая от текущих концентраций компонентов реакции, их теплоемкостей сi и объема реакционной смеси V. В качестве упрощающего предположения допустим, что объемная теплоемкость сV – величина постоянная, численно равная среднему значению теплоемкостей отдельных компонентов cV = (cA + cB + cC)/3. Окончательно дифференциальные уравнения балансов для данной реакции запишем в виде: 
(А)
Искомые зависимости концентрации и температуры реакции от времени получают при интегрировании системы уравнений (А) (также д/б зависимость к от времени, полученная на машине). Если в процессе реакции выделяется тепло, которое (частично) отводится через стенку реактора при помощи хладагента, то при составлении уравнений математической модели, кроме уже приведенных исходных данных, необходимо знать: коэффициент теплоотдачи через стенку l, поверхность теплообмена S, температуру хладагента Тx. В этом случае дифференциальное уравнение скорости изменения температуры реакционной массы имеет вид: 
(Б).
Скорость реакции описывается уравнением: (В). Уравнение (В) подставим в уравнение (Б) 
(Г). Совместное решение уравнений (Г) и (В) на машине позволяет изучить химическую реакцию, например, с выделением тепла при отводе избытка тепла. При этом можно варьировать S, l, температуру хладагента Тx.
Реакцию с тепловым эффектом иногда необходимо исследовать в условиях постоянной температуры. В этом случае тепло, выделяемое в ходе химической реакции, должно полностью отводиться через стенки реактора. При этом Т=const, следовательно, dT/dt=0, k(t)=const и уравнение (Г) можно преобразовать к виду: 
. С помощью этого уравнения можно найти закон программного изменения температуры хладагента, которое обеспечивает постоянство температуры реакционной массы. Здесь концентрация СА – переменная величина, поэтому, чтобы равенство не нарушалось, температура Тx должна изменяться по следующему закону: 
Теперь получаем закон изменения Тx от времени при постоянной к.
Моделирование гетерогенно-каталитических реакций
Работа заключается в ознакомлении с приемами составления кинетических уравнений гетерогенно-каталитических реакций и моделирования таких реакций на вычислительной машине. Обычно гетерогенно-каталитические процессы протекают в жидкой, газовой или паровой фазе при участии твердого катализатора. В случае газовой гетерогенно-каталитической реакции исходные реагенты и продукты реакции – газы. При их участии в реакции каждая молекула реагента последовательно проходит следующие стадии: диффузионный перенос из газовой среды к поверхности катализатора, адсорбцию на его поверхности, химическое превращение в адсорбированном слое, десорбцию продуктов реакции, диффузионный перенос продуктов реакции с поверхности катализатора в газовую среду. На скорость гетерогенно-каталитической реакции большое влияние оказывает площадь активной поверхности твердого катализатора, Для ее увеличения катализаторы обычно выполняют в виде зерен с сильно развитой пористостью. При этом кажущаяся поверхность зерен ничтожна по сравнению с поверхностью внутренних пор и каналов в зерне. Значения длины и диаметра внутренних ходов должны исключать сильное торможение диффузионно-транспортных стадий процесса (внутренняя диффузия). Однако, внешняя термодинамическая обстановка снаружи зерна катализатора не должна затруднять транспорт вещества к катализатору и от него (внешняя диффузия). Наиболее выгоден режим, при котором лимитирующей стадией, определяющей скорость гетерогенно-каталитической реакции, является собственно химическое превращение. В таком случае говорят, что процесс идет в кинетической области (в противоположность внутридиффузионной и внешнедиффузионной области). Однако, практически не всегда удается устранить диффузионное торможение.
Известны различные теоретические подходы к выводу кинетических уравнений. При этом скорость реакции u определяется как изменение числа молей dN (например, продукта реакции) за время dt при участи катализатора массой G.
Иногда скорость реакции записывают относительно единицы поверхности катализатора
S: 
.
Если гетерогенная каталитическая реакция является многокомпонентной, вид кинетической функции может оказаться достаточно громоздким. Здесь рассмотрено моделирование реакций с использованием кинетических представлений Ленгмюра –Хиншельвуда. Формы других кинетических уравнений, например Хоугенга и Ватсона, аналогичны рассматриваемой. Уравнения кинетики Ленгмюра – Хиншельвуда выводят на основе предположения об ограниченной активности поверхности катализатора. Предполагают, что химическое превращение может происходить только при участии молекул, попавших за счет адсорбции на активный центр катализатора. Принимают, что число активных центров на единице поверхности (поверхностная концентрация) ограничено. Кроме того, для упрощения считают, что каждый активный центр может удерживать лишь определенное число молекул (или атомов) реагирующего вещества (обычно одну). При таких предпосылках скорость химического превращения оказывается пропорциональной концентрациям реагирующих веществ, адсорбированным на поверхности, т.е. поверхностным концентрациям. Для описания зависимости поверхностной концентрации некоторого вещества от его концентрации в объеме окружающего газа используют уравнение изотермы адсорбции Ленгмюра. Для упрощения принимают условия равновесия адсорбции и десорбции. Скорость адсорбции ra некоторого компонента может быть принята пропорциональной его давлению Р и концентрации свободных активных центров, определяемой как разность между полной концентрацией активных центров Са и концентрацией занятых центров С: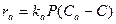 
. Скорость десорбции rd пропорциональна концентрации занятых активных центров С: 
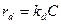. Предполагая равновесие между адсорбцией и десорбцией, т.е. приняв, что ra=rd, получаем: 
. Отсюда концентрация занятых активных центров С равна С = КРСа/(КЗ + 1) здесь К=ка/кд – константа равновесия адсорбции.
В практике моделирования гетерогенно-каталитических процессов вместо поверхностных концентраций активных центров используют относительные концентрации q = С/Са, называемые обычно степенью заполнения активных центров. Используя параметр q последнее уравнение можно записать следующим образом: q = КР/(1 + КР). Если процесс адсорбции сопровождается обратимой диссоциацией на n частиц, то скорости адсорбции ra и десорбции rd являются функциями n–й степени от соответствующих концентраций, тогда
(Д)
Если газовая фаза содержит несколько компонентов, адсорбируемых поверхностью катализатора, необходимо вычислить степень заполнения поверхности каждым компонентом. При этом следует учитывать, что концентрация свободных мест определяется разностью между полной концентрацией активных центров и суммой центров, занятых всеми компонентами. Например, при адсорбции двух газов (А и В) степени заполнения поверхности можно записать следующим образом:
qА = КАРА / (1 + КАРА + КВРВ) (З) и qВ = КВРВ / (1 + КАРА + КВРВ) (К)
При диссоциации адсорбируемых компонентов так же, как в уравнении (Д), появляются дробные степени. Например, при диссоциации компонента А на две частицы вместо уравнения (З) и (К) получаем:
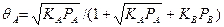(Л) и
(М).
Если в газовой среде присутствует инертный компонент, не участвующий в химической реакции, но адсорбируемый поверхностью, в знаменатель выражений типа (Д)-(М) добавляют соответствующее слагаемое. Как отмечалось выше, скорость химического превращения пропорциональна поверхностным концентрациям реагирующих компонентов: 
, где к – константа скорости реакции.
Рассмотрим, например, скорость реакции типа А + В ® М. При отсутствии диссоциации реагентов и без учета инертного компонента получаем:
W = kqAqB = kKAKBPAPB / (1 + KAPA + KBPB + KMPM)2.
Проведя аналогичные рассуждения, можно вывести кинетическое уравнение Ленгмюра – Хиншельвуда для более сложных случаев.
Если адсорбционные свойства компонентов реакции существенно различны, то вид уравнения Ленгмюра может быть изменен. Рассмотрим, например, реакцию вида А ®Р. Для этого случая уравнение Ленгмюра будет иметь вид 
(Н). Если реагирующий газ адсорбируется слабо, а продукт реакции – умеренно, то КАРА<< 1, и уравнение (Н) можно записать следующим образом: 
. Кинетическое уравнение для такого случая имеет вид: W = kFPA / (1 + KPPP), здесь kF = kKA – кажущаяся константа скорости реакции. В случае сильной адсорбции реагирующего вещества и продукта реакции можно пренебречь единицей в знаменателе уравнения (Н), тогда уравнение скорости имеет вид: W = kFPA / (KAPA + KPPP). При слабой адсорбции реагирующего вещества и сильной адсорбции продукта КАРА << 1 << КРРР. Следовательно, кинетическое уравнение примет вид: W = kFPA / (КPPP). Если допустить, что может происходить химическое взаимодействие адсорбированных молекул одного из реагентов с молекулами другого, приходящими из газовой фазы, то общий вид кинетической функции следует изменить на: 
.Примером кинетической функции такого вида может служить выражение скорости гидрохлорирования ацетилена (С2H2 + HCl ® C2H3Cl): 
. Скорость реакции определяется концентрацией ацетилена в газовой фазе (причем ацетилен практически нне адсорбируется на поверхности катализатора), а также поверхностной концентрацией хлористого водорода. Вследствие слабой адсорбции продукта реакции для расчета поверхностной концентрации хлористого водорода применяют уравнение, не учитывающее адсорбцию продукта. Для практических расчетов в ограниченной области режимных параметров часто используют аппроксимирующие степенные кинетические выражения, аналогичные формально-кинетическим уравнениям гомогенных реакций: W = kPaA×PbB×…×PmM, где a,b,m – частные порядки реакции. Так, например, скорость окисления водорода на палладиевом катализаторе прималой концентрации может быть описана следующим простым уравнением: 
. При моделировании реакций в неизотермических условиях следует учитывать зависимость коэффициентов адсорбции и константы скорости от температуры. Это, однако, значительно усложняет модель.
Моделирование гетерогенных каталитических реакций – более трудоемкий и сложный процесс, чем моделирование гомогенных реакций, т.к. кинетические функции в этом случае сильно нелинейны, и требуется большое число нелинейных решающих элементов. Почти обязательно использование блока деления; в ряде случаев необходимы также блоки извлечения корня или возведения в степень.
Задание9 Получить модель заданной гетерогенной каталитической реакции и снять кинетические кривые для периодического процесса в изотермических условиях. Промышленный процесс получения разбавленной азотной кислоты основан на каталитическом окислении кислородом оксида азота, содержащегося в нитрозных газах: 2 NO + O2® 2 NO2. Механизм процесса: 2NOгазÛ 2NOадсÛ (NO)2 адс (NO)2 адс + O2 газ® N2O4 адсÛ 2NO2 адс 2NO2 адсÛ 2NO2 газ. Скорость процесса определяется лимитирующей стадией взаимодействия кислорода газовой среды с активной формой адсорбированного оксида азота. Адсорбция кислорода незначительна по сравнению с адсорбцией оксида и диоксида азота. Уравнение кинетики имеет вид:
(О). При
моделировании реакции найти кривые для всех трех компонентов газовой фазы, если к=1.1×109 л3/(моль2×с×лкат), КNO=1.9×108 л2/моль2,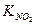 
=0.26 ×104 л/моль. Температура Т=200оС; давление атмосферное, начальные концентрации, %(объемн.): СNO(0)=1, 
(0)=5, 
(0)=0. Изменением объема компонентов в результате реакции пренебречь. Приведенное кинетическое уравнение требует подстановки в него мольных концентраций, в то время как в задании оговорены объемные проценты. Учитывая равные мольные объемы всех компонентов смеси, можно заключить, что при нормальных условиях С, моль/л = 4.47×10-4 С, %(объемн.). Таким образом, начальные концентрации реагентов в мольном выражении следующие:
CNO(0)=(273/(273+200))×4.47×10-4×1=2.56×10-4 моль/л
=(273/(273+200))×4.47×10-4×5=12.8×10-4 моль/л.
Для моделирования реакции необходимо составить программу по уравнению (О). Возводить в квадрат переменную СNO целесообразно с помощью блока перемножения. Текущие концентрации оксида азота и кислорода можно вычислять по стехиометрическим соотношениям: CNO(t) = CNO(0) - (t), 
= - 0.5 (t).
Исследование химических реакций
В работе изучаются приемы коррекции параметров математической модели на машине для получения адекватных моделей химических реакций. Предыдущие работы затрагивали вопросы прямого моделирования химических реакций: по известному механизму и на основе полной информации о кинетике реакции, определялись зависимости температуры и концентраций компонентов реакции от времени. При этом считалось, что результаты решения уравнений кинетики на машине равноценны полученным в ходе эксперимента кинетическим зависимостям, так как математическое описание реакции соответствует химическому процессу.
При изучении химической реакции в реальных условиях возникает проблема составления адекватного математического описания. Как правило, обсуждается несколько предполагаемых вариантов механизма реакции. Математические описания и, следовательно, модели этих вариантов различаются по числу элементарных стадий. При этом обычно в качестве неизвестных кинетических параметров математического описания выступают константы скорости и порядки отдельных стадий реакции, которые требуется определить. В пределах постулируемого механизма параметры модели подбирают, добиваясь максимального соответствия результатов моделирования экспериментальным данным. Чтобы установить адекватность математической модели реакции реальному химическому процессу, необходимо решить систему уравнений принятой математической модели и сравнить полученные результаты с аналогичными данными, найденными экспериментально. Эффективное решение этой задачи возможно при использовании поисковых методов, например, метода целенаправленного перебора вариантов, сопровождающегося оценкой удачности выбора констант в каждом из них.
Для определения кинетических параметров химической реакции на машине необходим некоторый критерий адекватности математической модели (часто, однако, оказывается достаточной визуальной оценки с помощью двухкоординатного регистрирующего прибора). Независимо от метода поиска неизвестных параметров, в качестве такого критерия чаще всего используют интегральную функцию ошибок D в виде критерия:
интегрально-разностного 
(Р) и
интегрально-квадратичного
, (П)
где Сie – экспериментальная зависимость концентрации i-го компонента от времени; Сip – рассчитанная (на машине) зависимость концентрации i-го компонента от времени; tn, tk – моменты времени, соответствующие началу и концу интегрирования.
Критерий (П) характеризуется пониженной чувствительностью к малым отклонениям (вследствие возведения разности в квадрат), в то время как критерий (Р) равномерно учитывает любые отклонения. Очевидно, чем меньше D, тем ближе экспериментальная зависимость к расчетной. Поэтому определение неизвестных параметров сводится к достижению минимума критерия D путем надлежащего выбора определяемых параметров. Независимо от вида критерия необходимо вычислять текущую разность значений концентрации, найденных экспериментально и рассчитанных в результате моделирования на машине.
1. Составить математическую модель химической реакции по известному механизму и запрограммировать уравнения математического описания для решения на машине.
2. Определить с помощью ЭВМ неизвестные константы (параметры модели).
3. Освоить моделирование реакции дробного порядка.
4. Найти порядок и константу скорости химической реакции.
Задание 10 Составить заключение об адекватности математического описания, используя метод неявных функций и исходя из предположения, что скорость превращения исходного вещества А в продукт В при постоянной температуре описывается кинетическим уравнением реакции первого порядка 
(С). Экспериментальные данные по концентрации исходного компонента реагента равны:
t, C 0 10 20 30 40 50 60 70 80
CАэ, кмоль/м3 1 0.6 0.39 0.24 0.15 0.10 0.06 0.03 0.015
В результате моделирования получаем зависимости k(t) и CA(t). В интервале t1 £ t £ t2 (t1 = 0, t2 = 70 c) коэффициент k=Const и, таким образом, модель адекватна реальному процессу. В интервале t2 < t £ t3 (t2=70 c, t3=100 c) происходит изменение константы скорости. Вероятно, экспериментальные данные в этой области содержат значительные погрешности – область малых концентраций. Таким образом, в интервале t1£ t £ t2 уравнение (С) хорошо аппроксимирует опытные данные при k=0.45.
Задание 11 Промоделировать реакцию, формальное ки-нетическое уравнение которой 
(Т), если к=3×10-3 л0.4/(моль0.4×с), n=1.4, С(0)=0.2 моль/л. Продифференцируем уравнение (Т) и определим вторую производную 
(У).
После подстановки уравнения (Т) в уравнение (У) получаем: 
. (Может быть целесообразно отказаться от вычисления первой производной?) Начальная скорость реакции С’(0) моль/(л×с), равна С’(0) = -кСn(0) =-3×10-3(0.2)1.4 = -3.15×10-4.
Задание 12 В ходе изучения термического разложения динитроксида на золоте при 990оС получены следующие кинетические данные:
время, мин 30 53 100
степень превращения, % 32 50 73
Определить порядок реакции n и константу скорости k с помощью вычислительной машины. Для решения задачи надо подготовить четыре вычислительных блока: блок, моделирующий собственно химическую реакцию, блок, воспроизводящий экспериментальную кривую,.
В уравнении (Т) производим замену: С = С0(1-x), где С0 – начальная концентрация. Получаем: (Т*). Для вычисления степени превращения x необходим дополнительный сумматор: - (-x = (1-x) – 1). (константа скорости реакции должна получиться 2.1×10-4 с-1.
Задание 13 Распределение молекул идеального газа по скоростям (распределение Максвелла).
;
Для 1 моля газа:
моль;
где u – скорость, k – константа Больцмана, T- температура К, m – масса молекулы, dN/du – плотность распределения частиц, т.е. доля частиц, скорость которых лежит в интервале от u до (u + du).
До написания программы необходимо выбрать систему единиц измерения для используемых и вычисляемых величин. К тому же нужно учесть некоторые фундаментальные константы, например: L – число Авогадро, молекулярная масса M=mL, универсальная газовая постоянная R=kL, равная 8.31441 Дж.(К×моль), отношение m/k заменено в вышеприведенной формуле на M/R.
Вводятся (задаются) температура, молекулярная масса, скорость (например, 300К, 28, 200 м/с и тогда плотность распределения составит 9.58969264×10-4 моль/(м/с), при увеличении скорости в 2 раза плотность распределения также увеличив. в 2 раза.)
Задание 14 Скорость истечения газа.
Еще один пример расчета по формулам - программа для вычисления скорости истечения идеального газа из сосуда под давлением. Скорость истечения зависит от давления внутри и вне сосуда, то молекулярной массы газа, от температуры и от отношения молярных теплоемкостей k=Cp/Cv (из-за адиабатического расширения).
;
где: w – скорость истечения, R – универсальная газовая постоянная, T – температура в сосуде, p – внешнее давление, p0 – давление в сосуде, M – молекулярная масса газа, k9 – вспомогательная величина, которую рассчитывают, исходя из Cp и Cv, k9=(k-1)/k.
При Т=293, массе 28.96, к=1.402, р=1.2, р0 =2.4, скорость составит 325.204413 м/с.
Задание 15 Интегрирование методом Монте-Карло.
При вычислении кратных интегралов метод М-К часто дает лучшие результаты, чем другие численные методы. Для начала рассмотрим f(x) при x=[a,b]. Площадь криволинейной трапеции равна площади прямоугольника, одна сторона которого равна среднему значению функции на заданном отрезке, а другая – длине этого отрезка. Вычисление среднего значения функции методом М-К: вычисляют значения функции в случайных точках внутри заданного отрезка и находят их сумму. После деления этой суммы на число точек получают среднее значение, которое ближе всего к истинному среднему значению функции на заданном отрезке, чем больше выбрано число случайных точек. В случае функции f(x,y) вычисляют значения функции в случайных точках (x,y), определяют среднее значение, которое умножают на площадь области интегрирования. Пример: вычислить интеграл f(x,y,z)=x2 + y2 + z2. Интегрируя по параллелепипеду (трехмерному интервалу). Значения этой конкретной функции можно определить аналитически и сравнить с расчетными значениями.
В выражении, стоящем справа от знака равенства, надо поставить верхние и нижние пределы интегрирования со знаками плюс и минус соответственно, т.е. как при вычислении определенного интеграла функции одной переменной.
Задание 16 Мольная теплоемкость металлов по Дебаю.
Согласно формуле, выведенной на основании теории Дебая, мольная теплоемкость металлов зависит от температуры Т и температуры Дебая q, которая является характеристическим свойством каждого металла. Эта формула содержит интеграл, который аналитическими методами невозможно вычислить, поэтому применим численное интегрирование, в частности, используем метод Симпсона. Строго говоря, теплоемкость (CV) зависит не от абсолютных значений Е и q, а от отношения q/T. Если обозначить q/Т = z, то формула Дебая принимает вид
.
С увеличением температуры мольная теплоемкость CV приближается к классическому значению 3R. Построить график этой зависимости.
Задание 17 Расчет вириального коэффициента на основе межмолекулярного потенциала.
Для описания состояния реального газа часто пользуются уравнением состояния идеального газа, к правой части которого добавлены слагаемые в виде степенного ряда по давлению. Коэффициенты этого степенного ряда называются вириальными коэффициентами. Если ряд оборвать на втором члене, то получится следующая формула:
PV = RT + B(T)P
В(Т) можно определить из экспериментальных данных по уравнению:
B(T) = ¶(PV)/¶P.
Размерность коэффициента В(Т) – ед. объема/моль. Отклонение поведения реального газа от идеального обусловлено межмолекулярным взаимодействием. Второй вириальный коэффициент можно рассчитать, исходя из межмолекулярного потенциала EP(r). Ради простоты атомы или молекулы будем считать шарообразными. Тогда на потенциал EP будет оказывать влияние только расстояние между частицами, а не их взаимная ориентация. Пусть межмолекулярный потенциал имеет вид потенциала Леннарда-Джонса:
,
r – расстояние между атомами; s - расстояние, на котором силы притяжения и отталкивания равны; x - глубина потенциальной ямы; n – соответствует члену, описывающему притяжение (обычно равно 6); m – соответствует члену, описывающему отталкивание (обычно равно 12).
Сила межмолекулярного взаимодействия K(r) в общем виде выражается как:
.
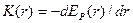Второй вириальный коэффициент В(Т) можно рассчитать по следующей формуле:
.
- Построить зависимость вторых вириальных коэффициентов различных веществ от температуры и от обратной температуры.
Задание 18 Вычислить CV металлов по формуле Дебая и заполнить таблицу по следующей форме:
| q/T | 0.01 | 0.1 | 0.5 | ||||
| CV |
Построить график зависимости CV никеля от температуры (температура Дебая 375 К).
Задание 19 Исходя из значений CV, рассчитать разность значений внутренней энергии при двух различных температурах по следующей формуле:
Значения CV вычислить по формуле Дебая. Для расчета DU необходимо составить программу для двойного интегрирования.
Задание 20 Зависимость СР(Т) от температуры описывается следующей формулой:
Вычислить DH, DS при двух произвольных температурах (например, при 78 К и 532 К).
Задание21 Пусть дана химическая реакция 
, скорость которой подчиняется кинетическому уравнению первого порядка: 
, где
t – время, k –константа скорости реакции. Зависимость k от температуры описывается уравнением Аррениуса:
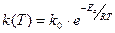
Пусть температура в реакторе (начальное значение 300 К) меняется со временем в соответствии с уравнением
,
TE – конечное значение температуры, q – постоянная времени, которая определяет скорость изменения температуры. Тогда константа скорости реакции будет также зависеть от времени:
.
Концентрацию А при постоянной температуре можно рассчитать по формуле:
,
Для неизотермических условий справедливо:
.
Составить программу, позволяющую выяснить зависимость концентрации А от [A]0, Ea, k0, TE, q, t.
Задание 22 Составить программу для летучести f в зависимости от давления p и температуры T, полагая, что для реальных газов выполняется соотношение Ван-дер-Ваальса:
,
Уравнение Ван-дер-Ваальса имеет вид:
.
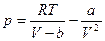Вычислить несколько примеров по выбору, исходные данные приведены в таблице.
| А/(л2атм×моль-2) | 100b/(л×моль-1) | |
| Бензол | 18.00 | 1.154 |
| Xe | 4.194 | 5.105 |
| H2O | 5.464 | 3.049 |
| CO2 | 3.592 | 4.261 |
Задание 23 В квантовой химии часто возникает необходимость вычислять интегралы перекрывания. Ниже рассмотрен гипотетический пример, на котором объясняется принцип вычисления интегралов перекрывания. Пусть дана одномерная волновая функция w(x): 
. Сначала рассчитывают нормировочный коэффициент N, который выбирают так, чтобы выполнялось следующее условие:
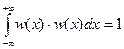. Для нормированной волновой функции интеграл перекрывания рассчитывают по формуле: 
.
А и В – расстояния от произвольной нулевой точки до атомов А и В соответственно; |А-В| - расстояние между атомами. Вычислить интегралы перекрытия при различных расстояниях между атомами.
Пусть имеются некоторая кислота и вода, которые диссоциируют по следующему механизму:
НА Û Н+ + А- (1)
Н2О Û Н+ + ОН- (2)
Соответствующие константы равновесия имеют вид 
(3) - константа диссоциации кислоты; 
(4) - ионное произведение воды.
Поскольку анион А- образуется только из кислоты НА, уравнение материального баланса по кислоте выглядит следующим образом:
[НА]o = [HA] + [A-] (5) – материальный баланс по кислоте.
Раствор электролита в целом электронейтрален, поэтому количество положительных и отрицательных ионов должно быть одинаково: [H+] = [A-] + [OH-] (6) – баланс по заряду. Если выражение для концентрации недиссоциированной кислоты [HA], найденное из уравнения (3), подставить в уравнение (5), то получится 
(7).
Если выражение для концентрации ионов ОН-, полученное из уравнения (4), подставить в уравнение (6), то выражение для А- примет вид: 
(8)
Если выражение (8) подставить в уравнение (7), то получится формула, в которую входят только константы равновесия, концентрация кислоты и концентрация ионов водорода:
.
Формула пересчета: log10(x) = ln(x)/ln(10).
Задание 24 Составить две таблицы или построить два графика, отражающие зависимость рН от концентрации кислоты при заданной и постоянной константе диссоциации, а также от константы диссоциации при заданной (постоянной) концентрации.
Задание 25 Написать программу для расчета рН буферного раствора и проанализировать, что произойдет, если к нему добавить сильную кислоту. Буферный раствор
Задание 26 раствор, содержащий слабую кислоту и соль этой кислоты. При добавлении не очень большого количества сильной кислоты значение рН раствора меняется в относительно небольших пределах. Количественно это можно описать следующим образом:
НА Û Н+ + А-
Н2О Û Р+ + ОН-
КА Û К+ + А- (диссоциирует полностью).
В качестве сильной кислоты можно взять соляную, которая полностью диссоциирует:
HClÛH+ + Cl-
константа диссоциации слабой кислоты;
ионное произведение воды.
Анион А- образуется из слабой кислоты и из соли этой кислоты, что отражено в уравнении материального баланса:
[HA]o + [KA]o = [HA] + [A-] материальный баланс по аниону;
вследствие полной диссоциации КА [KA]o = [K+] уравнение баланса по заряду имеет вид:
[H+] + [K+] = [A-] + [OH-] + [Cl-]. Если концентрацию недиссоциированной кислоты выразить из уравнения для Ка и подставить полученную формулу в уравнение материального баланса по аниону, то получим: 
. Выражение для концентрации ионов ОН-, найденное из уравнения ионного произведения воды, подставим в уравнение баланса по заряду. Полагая, что сильная кислота и ее соль полностью диссоциированы, после соответствующих преобразований получим: 
.
Совместное решение двух последних уравнений дает окончательную формулу, в которую входят константы равновесия, концентрации слабой кислоты, соли и сильной кислоты, а также концентрация ионов водорода:
.
Использовать в программе следующие входные данные: концентрации слабой кислоты и ее соли равны 1 моль/л. константа диссоциации слабой кислоты равна 1.85×10-5, ионное произведение воды равно 1×10-14. Ввести разные концентрации сильной кислоты и посмотреть, как при этом изменится рН раствора. Отобразить изменение рН в зависимости от концентрации сильной кислоты в виде графика.
Задание 27 Написать программу для расчета рН буферного раствора при добавлении к нему сильного основания.
Задание 28 Написать программу для расчета рН смеси растворов двух слабых кислот.
Задание 29 Пусть имеется раствор слабого электролита К2А, который непосредственно диссоциирует на три иона: 
. Согласно закону разбавления Оствальда, это равновесие можно описать следующей формулой: 
. Рассчитать степень диссоциации этого электролита при заданных значениях Кс и со (например, Кс =0.01 и со =0.001).
Задание 30 Дана обратимая реакция первого порядка: 
. Если проинтегрировать соответствующее кинетическое уравнение, то получится:
; где [A]o, [B]o – начальные (не равновесные) концентрации веществ; t – время; x – изменение концентрации вещества А и В: [A]=[A]o – x [B]=[B]o + x. Даны начальные концентрации веществ А и В и константа скорости к1. Кроме того, известно одно значение х в момент времени t. Написать программу для расчета константы скорости реакции к2.
Задание 31 Зависимость константы скорости реакции по теории Эйринга описывается следующей формулой: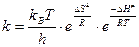 
, где kB – постоянная Больцмана, h – постоянная Планка.
Выбрать какие-нибудь значения для энтропии активации DS# (например, -11.8 кал/(моль×К)) и энтальпии активации DН# (например, 25000 кал/моль). Кроме того, следует задать константы скорости (например, 0.001 1/с). Найти температуру Т, которая соответствует выбранному значению к. Сравнить результат численного решения уравнения Эйринга с результатом аналитического расчета по приближенной формуле, которая не учитывает зависимость от температуры предэкспоненциального множителя. Для этого можно воспользоваться формулой Аррениуса: 
. Чтобы привести формулу Эйринга к виду уравнения Аррениуса, можно использовать среднюю температуру Тср.
и Ea = DH# + RTср.
Интегрирование кинетического уравнения первого порядка методом Монте-Карло.
Для реакции первого порядка (например, реакции распада или изомеризации) число реагирующих частиц в единицу времени пропорционально числу оставшихся частиц. Это дает в итоге (для очень большого числа частиц) следующее кинетическое уравнение:
, где Nt – число частиц в момент времени t; No – число частиц в момент времени 0;
