Графическое представление уравнения Бернулли для вязкой жидкости. Уравнение Бернулли для потока вязкой жидкости.
При переходе от ур. Бернулли для элемен. струйки идеальной ж. (
) к ур-ю потока реальной (вязкой) ж. необх. учитывать неравномерность распределения скоростей по сечению потока и потери энергии ж. на внутр. трение, (т.к. ж. вязкая). Это вызывает появление доп. потерь напора (энергии потока 
). Распр-е скоростей элемент. струек в потоке обычно неизвестно, поэтому в ур. Бернулли вводят поправочный коэфф. a, учитывающий изменение кин. энергии из-за неравномерности распр-я скоростей в живом сечении потока.
Коэфф. a называется коэфф. кин. энергии или коэфф. Кориолиса и определяется обычно опытным путем. Ур. Бернулли для потока реальной ж. с физ. точки зрения представляет ур. энерг. баланса. Теряемая энергия превращается в тепловую.
Т.о. ур. Бернулли для потока вязкой жидкости:
z – геод.высота/напор (удельн.пот.энергия положения)
– пьезометр.высота/напор (удельн.пот.энергия давления)
– скоростн.высота/напор (уд.кин.энергия)
– гидростат.напор (уд.пот.энергия)
– гидростатический (полный) напор
– разница уровней жидкости (по-тупому) или потери напора
a - коэфф. кин. Энергии.
Уравнение Бернулли для реальных газов.
По сравнению с движением ж.-ей движение газов хар-ся такой особенностью, как сжимаемость.
При выводе уравнения Бернулли для элементарной струйки идеальной жидкости было получено:
Для газов плотность вносить под знак дифф-ла нельзя, т. к. при течении сжимаемого газа надо учитывать
. При движении реальных газов, обладающих вязкостью, следует учитывать потери напора и уравнение Бернулли примет вид:
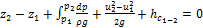(14.1)
Общ. случаем яв-ся политропический процесс (термодинам. процесс, во время кот. уд. теплоёмкость газа остаётся неизменной). Из ур. политропы 
, где n показатель политропы. Подставим это выражение в (14.1) и преобразуем:
Зная, что 
, а 
, можно придать этому уравнению вид:
z – геод.высота/напор (удельн.пот.энергия положения)
– пьезометр.высота/напор (удельн.пот.энергия давления)
– скоростн.высота/напор (уд.кин.энергия)
– температурный напор
R - газовая постоянная, равная универсальной газовой постоянной
T – абсолют.температура
– разница уровней жидкости (по-тупому) или потери напора
Виды сопротивлений. Основное уравнение равномерного движения жидкости.
В ур. Бернулли для потока реальной ж. присутствует слогаемое , называемое потерями напора на преодоление гидравлических сопротивлений. Потери учитываются: для прямых участков труб и каналов и для местных сопротивлений.
В случае прямолинейных участков потери наз-ся потерями по длине 
или линейными потерями напора.
Местные сопротивления: устройства, в кот. происходит резкая дефор-ция потока, кот. выраж-ся в изменении скорости или направления движения; это фасонные части, арматура, приборы и оборудование. Такие сопротивления называют местными, а потери напора называют местными потерями напора 
, или потерями напора на местные сопротивления.
При расчете значения сопротивлений суммируются:
