Рассмотрим n-канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, находящихся в системе или связанных с системой). Состояния системы:
— все каналы свободны;
—занят ровно один канал, остальные свободны;
—заняты ровно к каналов, остальные свободны;
—заняты все п каналов.
ГСП СМО представлен на рис. 5.7. Около стрелок поставлены интенсивности соответствующих потоков событий. По стрелкам слева направо систему переводит один и тот же поток — поток заявок с интенсивностью 
. Если система находится в состоянии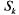 
(занято к каналов) и пришла новая заявка, то система переходит в состояние 
Рис. 5.7. ГСП для многоканальной СМО с отказами
Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево. Пусть система находится в состоянии 
(занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в 
; значит, поток событий, переводящий систему по стрелке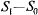 
, имеет интенсивность 
. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживания, переводящий систему по стрелке 
будет вдвое интенсивнее 
; если за-
нято k каналов — в к раз интенсивнее 
. Соответствующие интенсивности указаны у стрелок, ведущих справа налево.
Из рис. 5.7 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса размножения и гибели, рассмотренного выше.
Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:
(5.39)
Уравнения (5.39) называют уравнениями Эрланга. Поскольку при t = 0 система свободна, начальными условиями для их решения являются:
12. Наибольший интерес представляют предельные вероятности состояний 
характеризующие установившийся режим СМО (при 
). Для нахождения предельных вероятностей воспользуемся ранее полученными соотношениями (5.32)—(5.34), полученными для модели размножения и гибели. Согласно этим соотношениям,
(5.40)
В этих формулах интенсивность потока заявок 
и интенсивность потока обслуживании (для одного канала) 
не фигурируют по отдельности, а входят только своим отношением 
.
13. Это отношение обозначается 
:
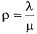
и называется приведенной интенсивностью потока заявок. Величина 
представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
С учетом этого обозначения, соотношения (5.40) принимают вид:
(5.41)
11. Соотношения (5.41) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров 
и n.
Имея вероятности состояний 
можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А и вероятность отказа 
.
Вероятность отказа. Заявка получает отказ, если приходит в момент, когда все и каналов заняты. Вероятность этого равна
(5.42)
Относительная пропускная способность. Вероятность того, что заявка будет принята к обслуживанию (относительная пропускная способность а), дополняет 
до единицы:
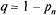
13. Абсолютная пропускная способность:
Среднее число заявок в системе. Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число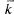 
. Величину 
можно вычислить через вероятности 
по формуле
как математическое ожидание дискретной случайной величины, однако проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которая уже известна. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу времени 
заявок; среднее число занятых каналов получится делением А на 
:
или, переходя к обозначению 
,
(5.43)
12. Установившийся режим обслуживания. Формулы Эрланга
Рассмотрим n-канальную систему массового обслуживания с отказами, на вход которой поступает простейший поток заявок с плотностью X; время обслуживания — показательное, с параметром х. Возникает вопрос: будет ли стационарным случайный процесс, протекающий в системе? Очевидно, что в начале, сразу после включения
системы в работу, протекающий в ней процесс еще не будет стационарным: в системе массового обслуживания (как и в любой динамической системе) возникнет так называемый «переходный», нестационарный процесс. Однако, спустя некоторое время, этот переходный процесс затухнет, и система перейдет на стационарный, так называемый «установившийся» режим, вероятностные характеристики которого уже не будут зависеть от времени.
Во многих задачах практики нас интересуют именно характеристики предельного установившегося режима обслуживания.
Можно доказать, что для любой системы с отказами такой предельный режим существует, т. е. что при t—>oo все вероятности
P0(t), P1(t)… Рn(t) стремятся к постоянным пределам p0, p1, pn,а все их производные — к нулю.
Чтобы найти предельные вероятности р0, pv..., рп (вероятности
состояний системы в установившемся режиме), заменим в уравнениях
все вероятности pk(t) их пределами рк, а все производные положим равными нулю. Получим систему уже не дифференциальных, а алгебраических уравнений
Решим систему относительно неизвестных р0, р1…pn. Из первого уравнения имеем
*
Из второго с учетом (*) – p2= 
Из третьего p3 = 
Для любого R<=n 
Теперь 
Она выражает все вероятности pk через р0.
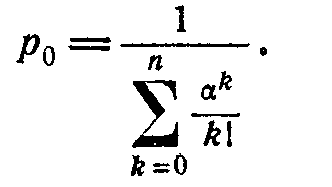
Эти формулы называются формулами Эрланга.
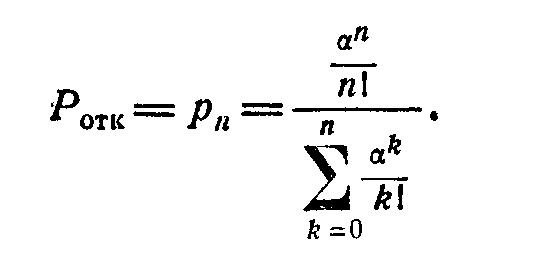Вероятность отказа (вероятность того, что поступившая заявка найдет все каналы занятыми).
Для одноканальной СМО вероятность отказа 
Относительная пропускная способность 
