Символдар
Атарының жинақты болуының қажетті шартын көрсетіңіз
A) 
Атарының жинақсыз болуының жеткілікті шартын көрсетіңіз
A) 
Гармоникалық қатары қандай болады?
A) жинақсыз
Атарының жинақтылық аймағын табыңыз
A) 
Атарының қосындысын табыңыз
A) 3
Атарды жинақтылыққа зерттеңіз
A) жинақсыз
Атардың жинақтылық аймағын табыңыз
A) [-3, 3)
Атардың жинақтылық аймағын табыңыз
A) (-1,5)
Атардың жинақтылық радиусын табыңыз
A) 1/6
Атардың жинақтылық радиусын табыңыз
A) +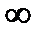 
Атардың жинақтылық аймағын табыңыз
A) 
Атардың жинақтылық аймағын табыңыз
A) 
Атардың жинақтылық аймағын табыңыз
A) (4,5; 5,5)
Атардың жинақтылық аймағын табыңыз
A) (-1,5; -0,5)
Атарын жинақтылыққа зерттеңіз
A) жинақсыз
Атарын жинақтылыққа зерттеңіз
A) жинақсыз
Атардыңтөртiншiмүшесiнтабыңыз
A) 1/17
Атардыңтөртiншiмүшесiнтабыңыз
A) 1/16
Атардыңбесіншімүшесiнтабыңыз
A) 10/13
Атарыныңалғашқыекімүшесініңқосындысынтабыңыз
A) 19/84
Атарыныңалғашқыекімүшесініңқосындысынтабыңыз
A) 9/8
Атарыныңалғашқыекімүшесініңқосындысынтабыңыз
A)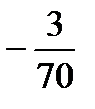 
Атарыныңалғашқыекімүшесініңқосындысынтабыңыз
A)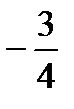 
Атарыныңүшіншіжәнебесіншімүшелерініңқосындысынтабыңыз
A)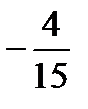 
Атардыңжалпымүшесінтабыңыз
A) 
Атардыңжалпымүшесінтабыңыз
A) 
Атардың жинақтылық радиусын табыңыз
A) 2
Атарын жинақтылыққа зерттеніз
А) жинақты
Атардыжинақтылыққазерттеңіз
A) жинақты
Атардыжинақтылыққазерттеңіз
A) жинақты
Атарын жинақтылыққа зерттеңіз
A) жинақты
Атарын жинақтылыққа зерттеңіз
A) жинақсыз
Функциясы үшін Маклорен қатарының жалпы мүшесі
A) 
Атарының жинақтылық аралығын табыңыз
A) (–2,2)
Атарының жинақтылық радиусын тап
А) 1
Атарының жинақтылық радиусын тап
А) 1/3
Атарының жинақтылық радиусын тап
А) 5
Атарының және мүшелерінің қосындысын табыңыз
А) 2/15
Атарының жинақталу интервалын табыңыз
А) 
Атарының жинақтылық интервалын табыңыз
А) (-2; 0)
Атарының жинақтылық интервалын табыңыз
А) (1; 3)
Атарының жинақтылық интервалын табыңыз
А) (-1; 1)
Атарының жалпы мүшесін табыңыз
А) 
Атарының қосындысын табыңыз
А) 0,5
Атарының бірінші және үшінші мүшелерінің айырымын табыңыз
А) 10
Атарының бірінші және үшінші мүшелерінің қосындысын табыңыз
А) 17,25
Атарының алғашқы екі мүшесінің қосындысын табыңыз
А) 
Атарының алғашқы үш мүшесінің қосындысын табыңыз
А) 69/140
Дәрежелік қатардың жинақтылық радиусын табыңыз
А) 4
Дәрежелік қатардың жинақтылық радиусын табыңыз
А) 5/3
Атарының қосындысын табыңыз
А) 5/6
Дәрежелік қатардың жинақталу радиусын табыңыз
А) 10
Және қатарлары жинақты, онда қатары туралы не айтуға болады
А) жинақты
Атарының екінші және төртінші мүшелерінің қосындысын табыңыз
A)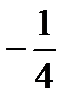 
Атарының екінші және үшінші мүшелерінің қосындысын табыңыз
A) 
Атарының екінші және үшінші мүшелерінің қосындысын табыңыз
А) -1
Атарының екінші және үшінші мүшелерінің қосындысын табыңыз
A) 13/27
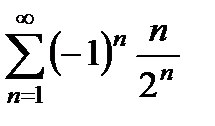қатарының алғашқы үш мүшесі мынадай:
A) 
қатарының жинақтылық радиусы тең
A) 1
дәрежелік қатарының жинақтылық радиусы тең:
A) 1.
қатары қандай қатар деп аталады:
A) Гармоникалық..
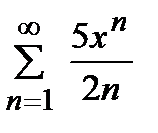дәрежелік қатарының жинақтылық радиусы тең:
A) 1.
атарын жинақтылыққа зерттеңіз
А) жинақсыз
