Экзамен будет письменным. Время для ответа – 60 мин. Экзаменационный билет состоит из 15 заданий

ЛИНЕЙНАЯ АЛГЕБРА И ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

I

1. Понятие матрицы и обозначение ее элементов. Квадратная, диагональная, единичная и треугольная матрицы. Равенство матриц. Транспонирование матриц. Операции сложения матриц и умножения матрицы на число.

2. Операция перемножения матриц и ее свойства. Перестановочные матрицы. Единичная матрица. Многочлены от матриц.

3. Определитель матрицы. Вычисление определителей второго и третьего порядков. Минор и алгебраическое дополнение элемента матрицы.

4. Разложение определителя по строке или столбцу. Вычисление определителей методом понижения порядка.

5. Свойства определителей. Вычисление определителей методом элементарных преобразований.

6. Решение системы линейных уравнений при помощи определителей. Правило Крамера. Условия применимости правила Крамера.

7. Обратная матрица; необходимое и достаточное условие ее существования. Нахождение обратной матрицы методом присоединенной матрицы.

8. Системы линейных уравнений. Совместные, несовместные, определенные и неопределенные системы.

9. Решение системы линейных уравнений методом исключения неизвестных (метод Гаусс). Общие и частные решения. Свободные и базисные переменные.

10. Ранг матрицы и методы его вычисления. Теорема о базисном миноре. Теорема Кронекера-Капелли.

II

1. Линейные операции над векторами. Коллинеарные и компланарные векторы.

2. Скалярное произведение векторов и его свойства. Необходимое и достаточное условие ортогональности двух ненулевых векторов. Вычисление скалярного произведения через координаты векторов. Формула для угла между векторами.

3. Правая левая тройка векторов. Векторное произведение векторов и его свойства. Необходимое и достаточное условие коллинеарности двух ненулевых векторов. Вычисление векторного произведения через координаты векторов. Геометрический смысл векторного произведения.

4. Смешанное произведение трех векторов и его свойства. Вычисление смешанного произведения векторов через координаты векторов. Геометрический смысл смешанного произведения векторов. Необходимое и достаточное условия компланарности трех ненулевых векторов.

5. Общее уравнение прямой на плоскости. Геометрический смысл коэффициентов уравнения.

6. Каноническое уравнение прямой на плоскости. Геометрический смысл коэффициентов уравнения. Параметрическая запись уравнения прямой.

7. Расположение прямых на плоскости. Условия параллельности и перпендикулярности прямых. Нахождение угла между двумя прямыми.

8. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов уравнения. Условия параллельности и перпендикулярности прямых.

9. Общее уравнение плоскости. Геометрический смысл коэффициентов уравнения. Вывод уравнения плоскости, проходящей через три заданные точки. Уравнение плоскости в отрезках.

10. Вывод канонического уравнения прямой в пространстве. Общие уравнения прямой. Взаимное расположение прямых в пространстве. Расположение прямых в пространстве. Условия параллельности, перпендикулярности, пересечения и скрещивания.

11. Кривые второго порядка. Классификация кривых второго порядка. Каноническая форма уравнений кривых второго порядка.

 

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1. Способы задания функции. Область определения функции.

2. Основные характеристики функции. Четные и нечетные функции. Периодические функции. Период функции.

3. Основные элементарные функции. Какие функции называются элементарными?

4. Определение предела функции в точке.

5. Бесконечно большие и бесконечно малые функции. Какая существует взаимосвязь между бесконечно большими и бесконечно малыми величинами?

6. Основные свойства пределов.

7. Раскрытие неопределенностей вида , , .

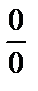8. Первый и второй замечательные пределы и следствия из них.

9. Эквивалентные бесконечно малые величины. Формулы эквивалентности.

10. Непрерывность функции. Классификация точек разрыва.

11. Определение производной функции одной переменной. Физический и геометрический смысл производной.

12. Правила дифференцирования. Таблица производных сложной функции.

13. Логарифмическое дифференцирование.

14. Производные первого и второго порядка от параметрических функций.

15. Производные первого и второго порядка от неявных функций.

16. Правило Лопиталя вычисления пределов. Раскрытие неопределенностей вида

17. Определение и геометрический смысл дифференциала функции одной переменной. Дифференциалы высших порядков

18. Монотонность функции. Экстремум функции. Необходимое и достаточное условие экстремума функции.

19. Выпуклые и вогнутые функции. Необходимое и достаточное условия существование точек перегиба.

20. Наименьшее и наибольшее значения функции на отрезке.

21. Асимптоты функции. Наклонные, горизонтальные и вертикальные асимптоты.

 

Экзамен будет письменным. Время для ответа – 60 мин. Экзаменационный билет состоит из 15 заданий.

Задания для подготовки:

1) Найти f (A), если

а) , ;

б) , ;

в) , .

2) а) Если () – решение системы линейных уравнений , то равно;

б) Решить систему ;

 

в) Если () – решение системы линейных уравнений , то равно.

3)

z

y

x

–4

а) Уравнение плоскости a, изображенной на рисунке, имеет вид

 

 

Для данной плоскости записать координаты нормального вектора.

б) Уравнение плоскости a, изображенной на рисунке, имеет

 

в) Записать уравнение плоскости, проходящей через точки А (1,-2,3); В (-2,1,1) и С (3,-1,4).

 

4) а) Угловой коэффициент прямой, проходящей через точки М₁ (2; 1) и М₂ (1; 3), равен

l

M0(1,-2)

б) Уравнение прямой l, изображенной на рисунке, имеет вид;

 

 

в) Уравнение прямой, проходящей через точку А(2,-3) параллельно вектору (2,0) имеет вид;

j = arctg2

x

y

г) Уравнение прямой l, изображенной на рисунке, имеет вид

 

д) Уравнение прямой, проходящей через точки А (2,-3,1) и В (1,2,-5) имеет вид. Для полученной прямой записать направляющий вектор.

5) а) Полуоси кривой второго порядка равны

x

y

-3

-2

б) Уравнение кривой второго порядка, изображенной на рисунке, имеет вид

 

 

6) Вычислить пределы:

 

а)	б)	в)
г)	д)	е)
ж)	з)	и)
к)	л)	м)

 

7)

y

x

b

a

с

x

y

b

a

с

y

b

x

a

y

x

b

a

с

а) Укажите вид графика функции, имеющей т. разрыва 2-го рода на отрезке [a; b]:

 

 

б) Построить график и определить характер точек разрыва:

8) а) Если , то значение равно;

б) Значение производной функции в точке равно;

в) Нормаль к графику функции образует с положительным направлением оси ОХ угол 135⁰, если она проведена в точке с координатами;

г) Касательная к графику функции в точке имеет вид.

 

 

9) Найти производные:

10)

x

y

a

b

y

a

b

x

Укажите вид графика функции , удовлетворяющей условию на отрезке :

a

b

y

x

a

b

y

x

 

Успешной сдачи экзамена!