Системы координат, их назначение и использование
Координатами называются угловые или линейные величины, определяющие положение точек на какой-либо поверхности или в пространстве.
Существует много различных систем координат. Для определения положения точек на земной поверхности применяются главным образом географические, плоские прямоугольные и полярные координаты.
Географические координаты
Географическими координатами называются угловые величины — широта и долгота, определяющие положение точек на земном шаре.
Географической широтой называется угол между отвесной линией в данной точке земной поверхности и плоскостью экватора. Широту принято обозначать греческой буквой j (фи). Очевидно, что для любой точки М на поверхности шара (рис 46) угол MCN будет широтой этой точки. Широты отсчитываются по дуге меридиана в обе стороны от экватора, начиная с 0° до 90°. В северном полушарии широты считаются северными, а в южном — южными.
Все точки, лежащие на одной географической параллели, имеют одинаковую широту, поэтому одна широта еще не определяет положения точки на земной поверхности. Необходимо знать вторую координату — долготу.
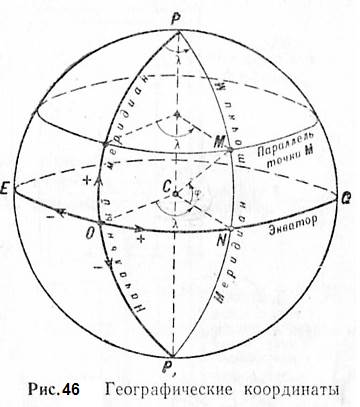
Географической долготой называется угол между плоскостью меридиана данной точки и плоскостью меридиана, условно принятого за начальный. Географическую долготу обычно обозначают греческой буквой l (ламбда). Угол OCN (рис. 46) будет долготой точки М. Как уже указывалось, у нас за начальный принят Гринвичский меридиан. Долготы отсчитываются по дуге экватора или параллели в обе стороны от начального меридиана, начиная с 0° до 180°. Долготы к востоку от начального меридиана до 180° называются восточными, а к западу — западными. Все точки, лежащие на одном меридиане, имеют одинаковую долготу.
Разность долгот двух пунктов показывает не только их взаимное расположение, но и разницу во времени в этих пунктах в один и тот же момент: каждые 15° по долготе соответствуют одному часу времени. Например, долгота г. Москва 37°37' (восточная), а г. Хабаровск 135°05', т. е. последний лежит восточнее на 97°28'. Таким образом, когда в Москве полдень (13 часов), в Хабаровске 19 часов 30 минут (по поясному времени 20 часов).
Определение географических координат по карте. На рис. 47 показано оформление рамок листов топографических карт. Как видно из рисунка, в углах рамки карты подписаны долготы меридианов и широты параллелей, образующих стороны этой рамки. Между внутренней и внешней рамками нанесена шкала, разбитая на минуты широты (по боковым сторонам рамки) и долготы (по верхней и нижней сторонам рамки).
Таким образом, чтобы определить широту какой-либо точки А на карте (рис. 47), надо через эту точку провести параллель, т. е. прямую, соединяющую одноименные деления (или их доли) на шкалах минут западной и восточной сторон рамки, а затем по одной из этих шкал отсчитать широту параллели. Это и будет широта определяемой точки А. Проводить при этом параллель через весь лист карты не требуется, а нужно лишь отметить наколом циркуля или коротким штрихом точку ее пересечения со шкалой минут, по которой будет производиться отсчет широты. Для отсчета широты надо сосчитать по шкале, сколько минут заключается между южной стороной рамки карты и параллельюопределяемой точки, и полученное число минут прибавить к широте южной стороны рамки.
Аналогично, пользуясь шкалами минут северной и южной сторон рамки карты, определяют и долготу точки. На рис. 48 широта точки А будет 54°58',6, а долгота 37°31',0 (восточная).
Для точного определения географических координат по карте необходимо иметь линейку длиной не менее 40 см.
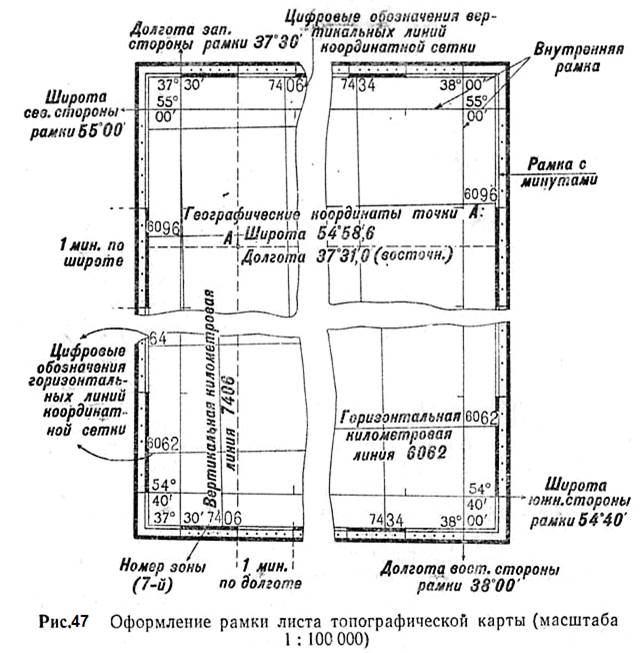
На картах последних лет издания минуты на шкалах широт и долгот дополнительно разбиты точками на 10-секундные деления, что позволяет определять географические координаты с точностью порядка 3—4" (см. рис. 47).
Плоские прямоугольные координаты
Плоскими прямоугольными координатами называются линейные величины — абсцисса и ордината, определяющие положение точек на плоскости.

Две взаимно перпендикулярные прямые X и У, относительно которых определяется положение точек (рис. 48), называются осями координат; из них ось X называется осью абсцисс, а ось Y — осью ординат. Точка пересечения осей — точка О — называется началом координат.
Оси координат делят плоскость на четыре четверти, счет которых ведется в топографии по ходу часовой стрелки от положительного направления оси X. За положительное направление осей координат принимается для оси абсцисс (X) направление на север, а для оси ординат (У) — навосток.
Положение любойточки М на плоскости относительно начала координат О (рис. 48) определяется кратчайшими расстояниями до нее от осей координат, измеренными в каких-либо мерах длины, например в метрах. Эти расстояния, являющиеся координатами точек, изобразятся, очевидно, отрезками прямых линий, перпендикулярных к одной из координатных осей и параллельных другой.
Координата X — абсцисса — вверх от оси У считается положительной, а вниз от нее — отрицательной.
Координата Y — ордината — вправо от оси X считается положительной, а влево от нее — отрицательной.
Таким образом, точки на рис. 49 будут иметь следующие координаты:
М1... x1= +2 м; y 1= +4 м
M2... x2 = - 4 м; у2 = +6 м
M3... x3 = - 2 м; у3 = - 4 м
M4... x4 = +6 м; у4 = - 6 м
Использование координатной сетки при работе на карте Координатная сетка весьма широко используется при работе на карте. Основное ее назначение — облегчить и упростить определение прямоугольных координат точек местности при целеуказании по карте. Вместе с тем она облегчает ориентирование на карте и указание на ней местоположения различных объектов при докладах, постановке задач, передаче распоряжений и составлении донесений. Наконец, она помогает быстро оценивать по карте на глаз расстояния и определять азимуты направлений.
Приближенное указание объектов и ориентирование на карте. Чтобы указать приближенно местоположение какого-нибудь пункта на карте, достаточно назвать квадрат сетки, в котором он расположен. Для этого надо прочитать за рамкой карты оцифровку вертикальной и горизонтальной километровых линий, образующих нижний левый (юго-западный) угол квадрата. При этом необходимо обязательно соблюдать следующее правило: сначала прочитывать и называть оцифровку (номер) горизонтальной километровой линии, а затем вертикальной, т. е. сначала называть абсциссу X, потом ординату У.

Например, командир, ориентирующий по карте своих подчиненных в обстановке, указывая местоположение точки с отметкой 118,0 (рис. 52), скажет:
«Квадрат сорок, сорок два: высота с отметкой 118,0». В письменных же донесениях и других документах этот пункт будет обозначаться так: «Высота с отметкой 118,0 (4042)».
Определение прямоугольных координат точек по карте. Если необходимо указать более точно положение какой- либо точки (цели) внутри квадрата, определяют ее координаты, отдельно абсциссу X и ординату У. Для
этого (рис. 53) записывают нижнюю километровую линию квадрата (т. е. 36), в котором находится определяемая точка М. Затем измеряют по масштабу в метрах расстояние (по перпендикуляру) до точки М от этой километровой линии, т. е. отрезок m и полученную величину (330 м) приписывают к координате линии. Так получается абсцисса X.
Для получения ординаты У записывают левую (вертикальную) сторону того же квадрата (т. е. 77) и затем приписывают к ней расстояние в метрах, измеренное от нее по перпендикуляру до определяемой точки, т. е. отрезок п (750 м).
Таким образом, в данном примере координаты точки М будут:
х = 36 330 м; y = 77 750 м.
Так как в данном случае при определении координат точки М цифровое обозначение километровых линий было записано не полностью, а лишь последними двумя их цифрами (36 и 77), то такие координаты называют сокращенными координатами точки М. В таком виде координаты обычно и записываются при определении их по карте.
Если же оцифровку километровых линий записывать полностью, то получим полные координаты, как они обычно записываются в специальных списках (каталогах) координат геодезических пунктов. В нашем примере (рис. 53) полные координаты точки М запишутся так:
x=6 136 330 м; y=5 577 750 м.
Измерение координат точек по карте и нанесение точек на карту по координатам производятся обычным способом, применяемым при измерении и откладывании прямых отрезков по масштабу карты, т. е. с помощью циркуля, или же по линейке с миллиметровыми делениями.






