1. Площа поверхні обертання.
2. Розв’язування типових задач.
Короткі теоретичні відомості
Площа поверхні, що утворюється при обертанні навколо вісі Ох кривої y=f(x), а≤х≤b, f(x)≥0, обчислюється за формулою
(1)
де функції 
і 
` неперервні на відрізку [a;b].
Якщо криву АВ задано параметрично рівняннями 
, де функції 
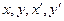неперервні на [α, β], то
, (2)
причому значення α параметра t відповідає точці А, а значення β -точці В.
Типові задачі
1. Обчислити площу поверхні, утвореної обертанням навколо вісі Ох однієї арки циклоїди 
.
За формулою (2) дістаємо
2. Обчислити площу поверхні, утвореної обертанням навколо вісі дуги кубічної параболи y=x3,обмеженої точками О(0;0) та А(
.
Знаходимо 
. За формулою (1) маємо
Питання для контролю вивченого матеріалу
1. Як обчислити площу поверхні, утвореної обертанням навколо вісі Ох кривої 
?
2. За якою формулою обчислюється поверхня, якщо криву задано параметрично?
3. Обчислити площі поверхонь, утворених обертанням навколо вісі Ох таких кривих:
а) параболи y2=x+2 від вершини до точки з абсцисою х=0, y³0;
б) дуги синусоїди від х=0 до х=1;
в) дуги астроїди х=cos3 t, y=sin3 t,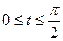 
.
Література
1. Соколенко О.І. Вища математика: Підручник – К.: Видавничий центр „Академія”, 2002. – 432с.
2. Валуцэ И.И. Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576с.
3. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. – К.: Вища школа, 1991. – 407с.: іл.
Тема 6. Довжина дуги кривої.
1. Поняття довжини дуги.
2. Обчислення довжини дуги кривої.
Короткі теоретичні відомості
М1 М2
А
B
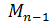
Довжиною L дуги АВ називається границя, до якої прямує периметр Рn вписаної в цю дугу ламаної, коли кількість n її ланок необмежено зростає, а найбільша із довжин S її ланок прямує до нуля: 
Якщо функції 
неперервні на відрізку [a;b], то довжина відповідної дуги кривої
(1)
Якщо криву АВ задано параметрично рівняннями x=x(t), y=y(t), 
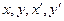, де функції неперервні на 
, причому точці А відповідає значення параметра 
,а точці В-значення 
, то довжина цієї кривої
(2)
Якщо криву задано в полярних координатах рівнянням 
, 
, то її довжина
(3)
де функції 
неперервні на відрізку 
Приклад 1. Обчислити довжину напівкубічної параболи у2=х3 між точками з абсцисами х=1 і x=2.
Диференціюючи рівняння кривої, знаходимо 
Тоді за формулою(1) 
. 
Приклад 2. Обчислити довжину кардіоїди 
.
Задана крива симетрична відносно полярної вісі, тому при зміні кута 
від 0 до 
полярний радіус опише половину кривої. Оскільки 
, обчислюємо за формулою (3) довжину кривої.
Питання для контролю вивченого матеріалу
1. Що називається довжиною дуги кривої та як вона обчислюється?
2. Обчислити довжини дуг таких кривих:
а) параболи 
між точками її перетину з віссю Ох;
б) кривої, заданої параметрично рівняннями 
в) першого витка спіралі 
Література
1. Соколенко О.І. Вища математика: Підручник.-К.: Видавничий центр “Академія”, 2002. - 432с.
2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие.-2-е изд., переработан и дополнен-М.:Наука, 1990. - 576с.: ил..
3. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. - К.: Вища школа, 1991. – 407с.: іл..
Література
1. Рудавський Ю. К., Костробій П. П., Луник Х. П., Уханська Д. В. Лінійна алгебра та аналітична геометрія: Навч. підручник – Львів: Видавництво «Бескид Біт», 2002. – 262 с.
2. Рудавський Ю. К., Костробій П. П., Уханська Д. В. Збірник задач з лінійної алгебри та аналітичної геометрії. – Львів: Видавництво «Бескид Біт», 2002. – 256 с.
3. Валєєв К. Г., Джалладова І. А. Вища математика: Навч. посібник: У 2-х ч. – К.: КНЕУ, 2001. – Ч. 1. – 546 с.
4. Лейфура В. М. та ін. Математика: Підручник для студентів екон. спеціальностей вищ. нав. закладів І-ІІ рівнів акредитації. – К.: Техніка, 2003. – 640 с. іл.
5. Соколенко О.І. Вища математика. – К.: Видавничий центр “Академія”, 2002. – 430 c.
6. Гаврильченко Х. І.,Полушкін С. П., Кропив’янський П. С., Овчинников П. П. Вища математика: Зб. задач: У 2 ч. Ч. 1: Лінійна і векторна алгебра. Аналітична геометрія. Вступ до математичного аналізу. Диференціальне та інтегральне числення: Навч. посібник для студ. вищ. техн. навч. закл.– 2-ге вид. стереотип.– К.: Техніка, 2004.-279с.: іл.
7. Шунда Н. М.. Томусяк А. А. Практикум з математичного аналізу: Вступ до аналізу. Диференціальне числення: Навч. посібник. – К.: Вища шк., 1992. – 303 с.: іл.
8. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб. Пособие.– М.: Наука. Гл. ред. физ.-мат. лит.,1990.– 576 с.
9. Бермант А.Ф. Краткий курс математического анализа для втузов. – М., 1964. – 664 с.
10. Лисичкин В.Т., Соловейчик И.Л. Математика: Учеб. Пособие для техникумов. – М.: Высш. Шк., 1991. – 480 с.
11. Геометрия. Учебник: В 2 ч. / Под ред. Яковлева Г.Н. – М.: Наука. Гл. ред. физ.-мат. лит., 1978.
12. Математика для техникумов. Алгебра и начала анализа: Учебник: В 2 ч. / Под ред. Яковлева Г.Н. – М.:Наука. Гл.ред. физ.-мат. лит., 1987.
13. Глаголев А.А., Солнцева Т.В. Курс высшей математики. Изд. 2-е, перераб. и доп. Учеб. пособие для вузов. – М.: Высш. шк., 1971. – 656 с.
14. Богомолов Н. В. Практические занятия по высшей математике. Учебное пособие для техникумов. – М.: Высшая школа, 1973. – 472 с.
15. Данко П. Е., Попов А. Г., Кожевников Т. Я. Высшая математика в упражнениях и задачах: Учебное пособие для студентов втузов. В 2-ух ч. – 4-е изд., испр. и доп. – М.: Высш. шк., 1986. – 304 с.
Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. – К.: Вища школа, 1991. –
