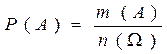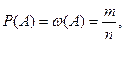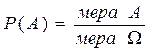| Аксиоматическое определение вероятности | Вероятностью события А называется численная мера объективной возможности появления события. Р(А)≥0; Р (Ω)=1 | |||
| Классическое определение вероятности | Вероятностью события А называется отношение числа исходов, благоприятствующих событию, к числу всех возможных равновозможных исходов эксперимента:
, где m(А) – число исходов, благоприятствующих событию А; n (Ω) – общее число исходов эксперимента. | |||
| Статистическое определение вероятности | Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях:
где ω(А) – относительная частота события А; m – число испытаний, в которых появилось событие А; n – общее число испытаний. | |||
| Геометрическое определение вероятности | Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области:
|
Алгоритм решения задач на классическое определение вероятности

Технология решения задач по алгоритму
На классическое определение вероятности

Задачи для тренинга
1. В лаборатории работает 20 человек, из них 55% женщин; 6 сотрудников должны уехать в командировку. Какова вероятность того, что среди них женщин и мужчин будет поровну?
2. В коробке находятся 6 одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки. Какова вероятность того, что сверла извлекутся в порядке возрастания их диаметра?
3. На пяти карточках написано по одной цифре: 1; 2; 3; 4; 5. Наугад выбирают две карточки. Какова вероятность того, что число на второй карточке больше, чем на первой?
4. Дано 6 карточек с буквами: Н, М, И, Я, Л, О. Найти вероятность того, что:
а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки;
б) получится слово МОЛНИЯ, если наугад одна за другой вынимаются 6 карточек и располагаются в порядке появления?
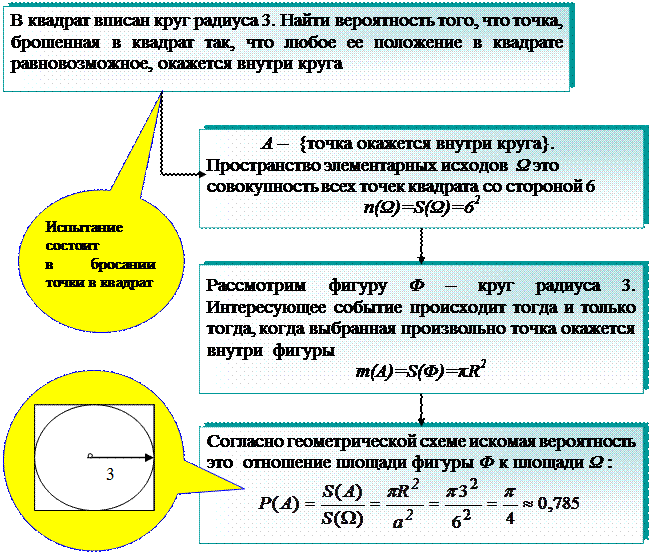
Геометрическое определение вероятности
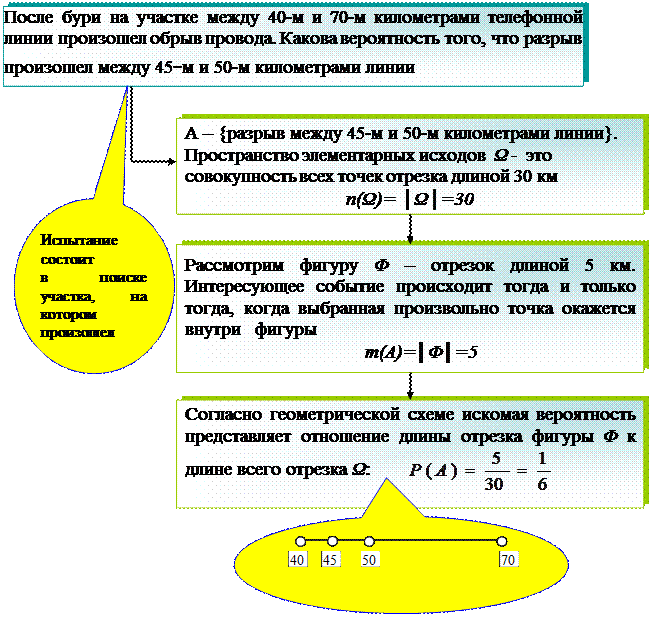
При решении задач на геометрическую вероятность придерживаются классической схемы решения, заменяя нахождение m(A) и n(Ω) вычислением соответствующих длин, площадей или объемов.
Технология решения задач по алгоритму
На геометрическое определение вероятности
Задачи для тренинга
1. В отрезке АВ длины 3 случайно появляется точка С. Определить вероятность того, что расстояние от точки С до В превосходит 1.
2. В прямоугольном броневом щите размером 2х1 м имеется невидимая для противника амбразура размером 10х10 см. Определить вероятность того, что пуля, попавшая в щит, попадет в амбразуру, если попадание в любую точку щита равновозможно.
3. В круг радиусом 5 вписан треугольник наибольшей площади. Определить вероятность попадания в треугольник точки, случайно брошенной в круг.
4. Минное заграждение состоит из мин, расположенных в одну линию на расстоянии 60 м одна от другой. Ширина корабля 20 м. Какова вероятность того, что корабль благополучно пройдет через заграждение?