6 Эмпирическая линия регрессии на графике представляет собой
Непрерывную кривую линию
7 Определение значения функции для произвольного значения аргумента вне пределов размаха его экспериментальных значений называется ……………… экстаполяция. данных
8 Определение значения функции для произвольного значения аргумента в пределах размаха его экспериментальных значений называется ……………… данных
9. Статистических показатели, построенные на основе параметров совокупности (среднего значения  и выборочной дисперсии s2x) называются
и выборочной дисперсии s2x) называются
параметрические,
10 Заполните числитель уравнения линейного коэффициента корреляции

10 Величина r=-0,15 – соответствует
Слабой обратной корреляционной связи
11 При преимущественном сочетании положительных отклонений (x) с положительными отклонениями (y), а отрицательных отклонений с отрицательными коэффициент корреляции будет
Больше 0
12 Величина коэффициента корреляции Пирсона может варьировать в пределах
Lt;r<1
13 Оцените существенность коэффициента корреляции (r) равного 0,85, при стандартной ошибке (sr) равном 0,5 и n=7 при 5% уровне значимости
tr=……………..; tst=………………; существенен да/нет
14 Несущественная при установленном критерия значимости величина коэффициента корреляции соответствует
Отсутствию связи установленной между функцией и аргументом
15 Статистических показатели,представляющие собой функции, зависящие от вариант совокупности с их частотами называются
Непараметрические
16 Величина r=0,25 – соответствует
Слабой прямой корреляционной связи
17 Величина r=1,0 – соответствует
Полной прямой корреляционной связи
18 При преимущественном сочетании положительных отклонений (x) с отрицательными отклонениями (y), а отрицательных отклонений с положительными коэффициент корреляции будет
Меньше 0
19 Оцените существенность коэффициента корреляции (r) равного 0,95, при стандартной ошибке (sr) равном 0,12 и n=6 при 5% уровне значимости
tr=……………..; tst=………………; существенен да/нет
20 Установите соответствие между уравнением и функцией
| Y=0,5x3-5 | Между функцией и аргументом существует функциональная связи |

| Между функцией и аргументом существует функциональная обратная линейная связь |
| y=f(x) | Между функцией и аргументом существует корреляционная связь |
| y=-2,5x+5 | Между функцией и аргументом существует функциональная прямая нелинейная связь |
6 Установите соответствие между уравнением и функцией
| y=0,5x-5 | Между функцией и аргументом существует функциональная связи |

| Между функцией и аргументом существует функциональная обратная линейная связь |
| y=f(x) | Между функцией и аргументом существует корреляционная связь |
| Y=-2,5x+5 | Между функцией и аргументом существует функциональная прямая линейная связь |
20 Установите соответствие между уравнением и функцией
| Y=2,5x+5 | Между функцией и аргументом существует функциональная связь |

| Между функцией и аргументом существует функциональная линейная связь |
| y=f(x) | Между функцией и аргументом существует корреляционная связь |
| y=2,5x2+5 | Между функцией и аргументом существует функциональная криволинейная связь |
21 Установите соответствие между уравнением и функцией
| Y=f(x) | Между функцией и аргументом существует функциональная связи |
| Y=2х-2,5x2+5 | Между функцией и аргументом существует корреляционная линейная связь |
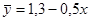
| Между функцией и аргументом существует корреляционная нелинейная связь |

| Между функцией и аргументом существует функциональная криволинейная связь |
22 Величина r=0,95 – соответствует




