Преобразование дискретных сигналов в аналоговые сигналы можно выполнить с помощью схемы цифроаналогового преобразования (рис. 3.59), например реализованной на аналоговом сумматоре (рис. 3.60), подключаемом к параллельному интерфейсу Centronics (LPT1 или LPT2).
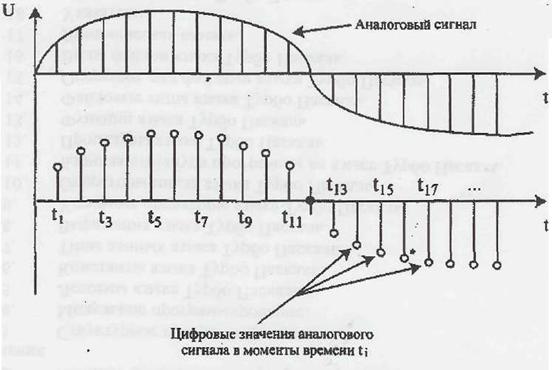
Рис. 3.60. Принцип действия аналогового сумматора
Поскольку ЭВМ работает с дискретными сигналами-импульсами, а звук представляет собой аналоговый (т.е. непрерывно изменяющийся) сигнал, для ввода звуковых сигналов необходимо их оцифровывать.
Способы оцифровки аналогового сигнала:
– аналого-цифровой преобразователь (АЦП), работающий по принципу измерения напряжения;
– клиппирование – время-импульсное кодирование аналогового сигнала;
– спектральный анализатор.
Квантование. Пусть в результате дискретизации непрерывного сигнала s (t) была получена последовательность узких импульсов, которая представляет собой АИМ-сигнал. Амплитуды импульсов равны в этом случае мгновенным значениям сигнала s (t) в моменты  , где i = 0, 1, 2, 3,...;
, где i = 0, 1, 2, 3,...;  – период следования импульсов, или интервал дискретизации.
– период следования импульсов, или интервал дискретизации.

Коды цифровой информации практически не меняются при многократной перезаписи или копировании информации. Шумы могут повлиять на физические уровни сигнала. Но они практически не влияют на логические уровни этого сигнала. Например, логический 0 может быть в пределах от 0 до 1 В, а логическая 1 – от 2,5 до 5 В. В результате, если уровни сигнала не выходят за эти пределы, то появляется возможность многократного тиражирования цифровой информации вне зависимости от числа копий и при сохранении качества записи.
Схема организации телеграфной связи.

Фазовая модуляция в цифровой системе связи.
Фа́зовая модуля́ция — один из видов модуляции колебаний, при которой фаза несущего колебания управляется информационным сигналом. Фазомодулированный сигнал  имеет следующий вид:
имеет следующий вид:
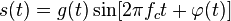 ,
,
где  — огибающая сигнала;
— огибающая сигнала; 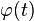 является модулирующим сигналом;
является модулирующим сигналом; 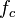 — частота несущего сигнала; t — время.
— частота несущего сигнала; t — время.
Фазовая модуляция, не связанная с начальной фазой несущего сигнала, называется относительной фазовой модуляцией (ОФМ).
Работы Хартли и Винера.
Теорема Шеннона — Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временно́го аналогового канала коммуникаций, искажённого гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанной полосой пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли. Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что пропускная способность канала 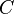 , означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала
, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала 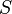 через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности
через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности 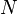 равна:
равна:
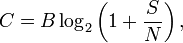
где
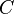 — пропускная способность канала, бит/с;
— пропускная способность канала, бит/с;
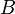 — полоса пропускания канала, Гц;
— полоса пропускания канала, Гц;
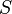 — полная мощность сигнала над полосой пропускания, Вт или В²;
— полная мощность сигнала над полосой пропускания, Вт или В²;
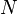 — полная шумовая мощность над полосой пропускания, Вт или В²;
— полная шумовая мощность над полосой пропускания, Вт или В²;
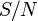 — частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.
— частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.






