Розв’язання завдань ІІ етапу Всеукраїнської олімпіади
6 клас
1. Знайдіть найбільший спільний дільник чисел  та
та  .
.
Відповідь:  .
.
Розв’язання. Перевіримо, що друге число діляться націло на  . Дійсно:
. Дійсно:
 – ділиться на
– ділиться на  . З властивостей НСД число
. З властивостей НСД число  і є шуканим НСД.
і є шуканим НСД.
 2. Є три попарно різних натуральних числа
2. Є три попарно різних натуральних числа  . Доведіть, що числа
. Доведіть, що числа  ,
,  та
та  не можуть бути трьома послідовними натуральними числами.
не можуть бути трьома послідовними натуральними числами.
Розв’язання. Якщо усі три числа додати та поділити на 3, то вийде їх середнє арифметичне, воно дорівнює з одного боку
 ,
,
а з іншого боку воно дорівнює середньому з цих трьох послідовних чисел.
Таким чином одне з чисел дорівнює  . Наприклад, це
. Наприклад, це  , тому
, тому 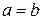 . А це суперечить тому, що усі 3 числа попарно різні.
. А це суперечить тому, що усі 3 числа попарно різні.
3. На папері у клітину нарисований квадрат розміром  клітин. Розріжте його по лініях клітин таким чином, щоб серед отриманих 5 частин
клітин. Розріжте його по лініях клітин таким чином, щоб серед отриманих 5 частин  та
та  (рис. 1) найбільшу площу мала частина
(рис. 1) найбільшу площу мала частина  , а найбільший периметр – частина
, а найбільший периметр – частина  .
.

Розв’язання. Приклад зображений на рис. 2.
4. Числа  переставили у деякому порядку і отримали набір чисел
переставили у деякому порядку і отримали набір чисел  . Чи обов’язково число
. Чи обов’язково число  ділиться націло на
ділиться націло на
а)  ; б)
; б)  ?
?
Відповідь: а) так; б) ні.
Розв’язання. а) Оскільки серед 2013 чисел 1007 непарних та 1006 парних, то обов’язково в одній з пар буде сума двох непарних чисел, яка кратна  , а тому й весь добуток є парним, тобто ділиться на
, а тому й весь добуток є парним, тобто ділиться на  .
.
б) Розглянемо таку перестановку чисел:
 .
.
Для неї вираз у кожній з дужок, окрім останньої, дорівнює непарному числу  , а тому й добуток цих чисел буде непарним. Остання дужка дає число
, а тому й добуток цих чисел буде непарним. Остання дужка дає число  , яке на
, яке на  не ділиться. Таким чином весь добуток на
не ділиться. Таким чином весь добуток на  не ділиться.
не ділиться.
7 клас
1. Розв’яжіть рівняння:  .
.
Відповідь:  .
.
Розв’язання. Зрозуміло, що 

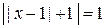 , оскільки
, оскільки  , то далі маємо, що
, то далі маємо, що 



 .
.
2. Чи існують натуральні числа 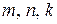 , які задовольняють рівність:
, які задовольняють рівність:
 ?
?
Відповідь: не існують.
Розв’язання. Оскільки  , то
, то  , аналогічно:
, аналогічно:  , то
, то  та
та 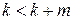 , то
, то  . Звідси
. Звідси  , тобто рівність не можлива.
, тобто рівність не можлива.
3. Знайдіть усі такі трицифрові числа, які при множенні на  стають точним кубом натурального числа.
стають точним кубом натурального числа.
Відповідь:  .
.
Розв’язання. Зрозуміло, що воно повинно ділитись на  . Решта множників повинні бути кубами натуральних чисел. Випишемо послідовно ці куби та подивимось, чому дорівнює добуток цих чисел на
. Решта множників повинні бути кубами натуральних чисел. Випишемо послідовно ці куби та подивимось, чому дорівнює добуток цих чисел на  .
.
 ,
,  – двоцифрове число, умову не задовольняє.
– двоцифрове число, умову не задовольняє.
 ,
,  – трицифрове число, умову задовольняє.
– трицифрове число, умову задовольняє.
 ,
,  – чотирицифрове число, умову не задовольняє.
– чотирицифрове число, умову не задовольняє.
Зрозуміло, що більші числа тим паче умову не задовольняють.
4. У трикутнику  проведена бісектриса
проведена бісектриса  . Через точку
. Через точку  проведена пряма, що перпендикулярна відрізку
проведена пряма, що перпендикулярна відрізку  і перетинає сторону
і перетинає сторону  у точці
у точці  . Доведіть, що
. Доведіть, що  .
.
 Розв’язання. Позначимо точку перетину
Розв’язання. Позначимо точку перетину  та
та  через
через  (рис. 3). Оскільки
(рис. 3). Оскільки  , то у
, то у  відрізок
відрізок  є бісектрисою та висотою одночасно, тому
є бісектрисою та висотою одночасно, тому  , тому
, тому  , тому у трикутнику
, тому у трикутнику  відрізок
відрізок 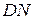 є одночасно висотою та медіаною, тому він рівнобедрений, тобто
є одночасно висотою та медіаною, тому він рівнобедрений, тобто  .
.
5. У малому залі кінотеатру є 10 рядів по 8 крісел, які розставлені у вигляді прямокутника. На кожному місці сидить глядач, який має рівно 100 гривень по 1 гривні. Якщо протягом сеансу хтось чихає, то він роздає по 1 гривні кожному з своїх сусідів. Сусідами вважають ті, хто сидить поруч зліва чи справа, або рівно позаду, або рівно попереду, тобто у кожного глядача є від 2-х до 4-х сусідів. Відомо, що Петрик чхнув протягом сеансу принаймні 1 раз. Яка найменша кількість чхань з урахуванням чхання Петрика могла бути протягом сеансу, якщо по завершенню у кожного глядача так і залишилось 100 гривень?
Відповідь: 80.
Розв’язання. Спочатку покажемо, що кожний глядач чхнув принаймні 1 раз. Якщо хтось не чхнув, щоб у нього залишились усі 100 гривень, він не повинен отримати гривню від жодного сусіда, тому його сусіди не чхали. Так само сусіди цих сусідів також не мали чхати і так далі. Виходить, що жодна людина не чхала.
Тепер покажемо, що якщо кожний глядач чхне рівно 1 раз, то кількість грошей у кожного не зміниться. Нехай вони чхнуть у довільному порядку. Тоді кожен віддасть стільки гривень, скільки у нього сусідів, так само і отримає рівно стільки гривень, скільки у нього сусідів.
Твердження доведене.
8 клас
1. Знайдіть різницю між сумою усіх парних чисел від 2 до 100 та сумою усіх непарних чисел від 1 до 99.
Відповідь:  .
.
Розв’язання. Розіб’ємо усі числа на пари.  , оскільки там усього 50 пар чисел.
, оскільки там усього 50 пар чисел.
2. Для яких цифр  п’ятицифрові числа
п’ятицифрові числа  та
та  є послідовними натуральними числами.
є послідовними натуральними числами.
Відповідь:  або
або  .
.
Розв’язання. Якщо число закінчується не на  , то при додаванні
, то при додаванні  , змінюється лише остання цифра. Таким чином треба розглянути лише варіанти
, змінюється лише остання цифра. Таким чином треба розглянути лише варіанти  або
або  . Очевидно тоді, що також
. Очевидно тоді, що також  та
та  відповідно.
відповідно.
Якщо  , то повинна виконуватись рівність:
, то повинна виконуватись рівність:  , тоді четверта справа цифра числа, що у правій частині останньої рівності повинна бути
, тоді четверта справа цифра числа, що у правій частині останньої рівності повинна бути  , тобто
, тобто  і ми маємо таку рівність:
і ми маємо таку рівність:
 .
.
Якщо  , то повинна виконуватись рівність:
, то повинна виконуватись рівність:  , тоді четверта справа цифра числа, що у лівій частині останньої рівності повинна бути
, тоді четверта справа цифра числа, що у лівій частині останньої рівності повинна бути  , тобто
, тобто  і ми маємо таку рівність:
і ми маємо таку рівність:
 .
.
 3. Задані 2013 чисел. Відомо, що сума будь-яких 11 з цих чисел – додатна. Чи обов’язково сума усіх 2013 чисел також додатна?
3. Задані 2013 чисел. Відомо, що сума будь-яких 11 з цих чисел – додатна. Чи обов’язково сума усіх 2013 чисел також додатна?
Відповідь: Обов’язково.
Розв’язання. Виберемо 11 найменших серед заданих чисел. Тоді їх сума – додатна. Але тоді усі інші числа – додатні. Бо якщо якесь з них, наприклад,  , а серед обраних 11 числах усі не перевищують
, а серед обраних 11 числах усі не перевищують  , то їх сума також недодатна. Таким чином одержали суперечність. Звідси висновок, сума найменших 11 чисел додатна. і усі інші числа також додатні. Тому сума усіх чисел – додатна.
, то їх сума також недодатна. Таким чином одержали суперечність. Звідси висновок, сума найменших 11 чисел додатна. і усі інші числа також додатні. Тому сума усіх чисел – додатна.
4. У опуклому чотирикутнику  сторона
сторона  видна з середини сторони
видна з середини сторони  під прямим кутом. Доведіть, що
під прямим кутом. Доведіть, що  .
.
Розв’язання. Позначимо середину сторони  через
через  , проведемо промені
, проведемо промені  та
та  , які паралельні відповідно прямим
, які паралельні відповідно прямим  та
та  , які перетинаються у точці
, які перетинаються у точці  (рис. 4). Зрозуміло за побудовою, що
(рис. 4). Зрозуміло за побудовою, що  – прямокутний. Тоді
– прямокутний. Тоді  – серединний перпендикуляр до
– серединний перпендикуляр до  , а
, а  – серединний перпендикуляр до
– серединний перпендикуляр до  , тому
, тому 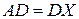 ,
,  , звідки
, звідки
 ,
,
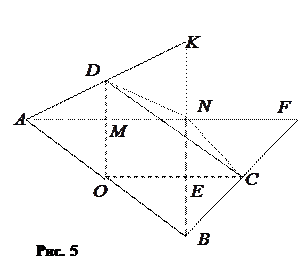 що й треба було довести.
що й треба було довести.
Альтернативне розв’язання. Відкладемо на променях  та
та  відрізки
відрізки  та
та  відповідно (рис. 5), для яких
відповідно (рис. 5), для яких 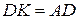 ,
,  . Тоді
. Тоді  та
та  – середні лінії
– середні лінії 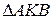 та
та  відповідно. Позначимо,
відповідно. Позначимо,  ,
,  ,
,  , тоді
, тоді  – прямокутник. Тоді маємо, що
– прямокутник. Тоді маємо, що  та
та  – прямокутні. В них
– прямокутні. В них 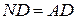 та
та  , звідки з нерівності трикутника і маємо шукане:
, звідки з нерівності трикутника і маємо шукане: 
5. На шалькових терезах розкладені гирі вагою 1, 2, 3,...,  ,
, 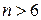 таким чином, що ваги знаходяться у рівновазі. Чи завжди можна зняти 3 гирі з терезів таким чином, щоб терези залишилися у рівновазі?
таким чином, що ваги знаходяться у рівновазі. Чи завжди можна зняти 3 гирі з терезів таким чином, щоб терези залишилися у рівновазі?
Відповідь: Завжди.
Розв’язання. Якщо для деякого  одна гиря
одна гиря  розташована на одній шальці терезів, а на іншій – гирі
розташована на одній шальці терезів, а на іншій – гирі  та
та  , то достатньо зняти оці 3 гирі і вимога задоволена.
, то достатньо зняти оці 3 гирі і вимога задоволена.
Якщо така ситуація не виконується, то розглянемо ту шальку терезів, де знаходиться гиря  , а також гирю, з найменшою вагою більшою
, а також гирю, з найменшою вагою більшою  . Нехай ця вага
. Нехай ця вага  . Тоді на цій шальці розташовані усі гирі вагою
. Тоді на цій шальці розташовані усі гирі вагою  . Зауважимо, що
. Зауважимо, що  , бо інакше на одній шальці лише 2 гирі
, бо інакше на одній шальці лише 2 гирі  та
та  , а на інших – усі інші, а вони мають більше вагу:
, а на інших – усі інші, а вони мають більше вагу:  . Тоді гирі розкладені на шальках таким чином:
. Тоді гирі розкладені на шальках таким чином:  та
та  . З цього очевидно, що
. З цього очевидно, що  , бо інакше рівності не буде. Але тоді на різних шальках розташовані гирі
, бо інакше рівності не буде. Але тоді на різних шальках розташовані гирі 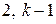 , а на іншій –
, а на іншій –  , які й можна зняти.
, які й можна зняти.
9 клас
1. Розв’яжіть рівняння:  .
.
Відповідь:  .
.
Розв’язання. Оскільки  , то задане рівняння можна переписати у вигляді:
, то задане рівняння можна переписати у вигляді:  , або
, або  , це рівносильне умові
, це рівносильне умові 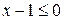 , тобто розв’язком рівняння є множина чисел
, тобто розв’язком рівняння є множина чисел  .
.
2. Знайдіть усі шестицифрові числа, які мають вигляд  та діляться націло на 45.
та діляться націло на 45.
Відповідь:  та
та 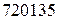 .
.
Розв’язання. Зрозуміло, що ці числа повинні бути кратними 9 та 5. Розглянемо два випадки. Якщо воно закінчується на 0, тобто  , то його сума цифр дорівнює
, то його сума цифр дорівнює  . Тому для виконання умови повинно
. Тому для виконання умови повинно  . Якщо воно
. Якщо воно  , то його сума цифр дорівнює
, то його сума цифр дорівнює  і повинно бути
і повинно бути  . Таким чином маємо дві відповіді.
. Таким чином маємо дві відповіді.

3. У квадраті розміром 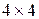 клітин деякі клітини зафарбовані у чорний колір. При цьому виявилось, що жодна чорна клітина не має суміжної сторони більше ніж з однією іншою чорною клітиною? Яка найбільша кількість клітин могла бути зафарбована у чорний колір?
клітин деякі клітини зафарбовані у чорний колір. При цьому виявилось, що жодна чорна клітина не має суміжної сторони більше ніж з однією іншою чорною клітиною? Яка найбільша кількість клітин могла бути зафарбована у чорний колір?
Відповідь:  .
.
 Розв’язання. Приклад, що належним чином можна зафарбувати
Розв’язання. Приклад, що належним чином можна зафарбувати  квадратиків зображений на рис. 6. Припустимо, що було зафарбовано більше, ніж 8, тоді принаймні у одному з чотирьох квадратів
квадратиків зображений на рис. 6. Припустимо, що було зафарбовано більше, ніж 8, тоді принаймні у одному з чотирьох квадратів  було зафарбовано не менше трьох клітин (рис. 7). Але тоді хоча б одна з них має суміжні сторони з двома іншими чорними клітинами. Одержана суперечність завершує доведення.
було зафарбовано не менше трьох клітин (рис. 7). Але тоді хоча б одна з них має суміжні сторони з двома іншими чорними клітинами. Одержана суперечність завершує доведення.
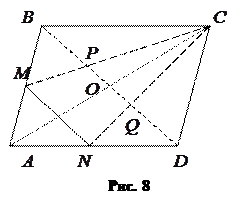 4. На діагоналі
4. На діагоналі  паралелограма
паралелограма  вибрані точки
вибрані точки 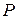 та
та  таким чином, що
таким чином, що  . Прямі
. Прямі  та
та  перетинають сторони
перетинають сторони  та
та  відповідно у точках
відповідно у точках  та
та  . Знайдіть відношення
. Знайдіть відношення  .
.
Відповідь:  .
.
Розв’язання. Проведемо діагональ 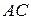 , тоді точка перетину діагоналей
, тоді точка перетину діагоналей  – ділить обидві діагоналі навпіл (рис. 8). Тоді для
– ділить обидві діагоналі навпіл (рис. 8). Тоді для  відрізок
відрізок 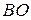 – медіана, а точка
– медіана, а точка 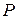 задовольняє умови
задовольняє умови  , тобто
, тобто 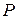 – точка перетину медіан
– точка перетину медіан  . Тому
. Тому  – також медіана
– також медіана  , а тому
, а тому  – середина сторони
– середина сторони  , аналогічно
, аналогічно  – середина сторони
– середина сторони  . Тому
. Тому  – середня лінія
– середня лінія  , звідси і випливає, що
, звідси і випливає, що  .
.
5. Для функції  ,
, 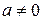 справджується умова
справджується умова  . Доведіть, що вона має два нулі.
. Доведіть, що вона має два нулі.
Розв’язання. Оскільки задану умову можна переписати у такому вигляді:


 .
.
А останню умову запишемо у такому вигляді  . Таким чином, або
. Таким чином, або  і парабола має два дійсних корені, або ці значення мають різні знаки, звідки також випливає, що вона має два дійсних корені.
і парабола має два дійсних корені, або ці значення мають різні знаки, звідки також випливає, що вона має два дійсних корені.
10 клас
1. Розв’яжіть рівняння:  .
.
Відповідь:  .
.
Розв’язання. Оскільки 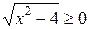 , то розглянемо два випадки.
, то розглянемо два випадки.
Перший випадок.  , звідки
, звідки  – розв’язки.
– розв’язки.
Другий випадок.  , звідки
, звідки  . Тоді задане в умові рівняння можна переписати таким чином:
. Тоді задане в умові рівняння можна переписати таким чином:  . Звідси випливає, що розв’язком останнього рівняння є проміжок
. Звідси випливає, що розв’язком останнього рівняння є проміжок  . З урахуванням першого випадку та умови
. З урахуванням першого випадку та умови  маємо наведену відповідь.
маємо наведену відповідь.
2. Дійсні числа  задовольняють рівність:
задовольняють рівність:
 .
.
Доведіть, що принаймні два з них рівні за модулем.
Розв’язання. Перепише рівність таким чином:
 .
.
Якщо  , то твердження доведене, бо
, то твердження доведене, бо  . Інакше, скоротимо на
. Інакше, скоротимо на  і будемо мати, що
і будемо мати, що
 або
або  ,
,
звідки й випливає, що або  , або
, або  . Твердження доведене.
. Твердження доведене.
3. Автобусні білети мають шестицифрові номери від 000000 до 999999. білет називається щасливим, якщо у нього сума перших трьох цифр дорівнює сумі останніх трьох. Назвемо білет суперщасливим, якщо він щасливий та серед цього цифр є чотири цифри 7, які йдуть поспіль (7777). Скільки усього існує суперщасливих номерів білетів серед усіх можливих?
Відповідь: 18.
Розв’язання. Розглянемо два випадки.
1 випадок. Комбінація 7777 йде посередині. Тоді, щоб білет став щасливим треба, щоб перша та останні цифри співпадали. Тому таких номерів рівно 10.
 2 випадок. Цифри 7777 йдуть на початку числа. Така ж кількість чисел, коли ці цифри йдуть наприкінці числа. Тоді дві останні цифри у сумі повинні давати 14. Таких комбінацій усього: 95, 86, 68 та 59. Тут не пишемо комбінацію 77, бо тоді маємо число 777777, яке вже враховане у першому випадку.
2 випадок. Цифри 7777 йдуть на початку числа. Така ж кількість чисел, коли ці цифри йдуть наприкінці числа. Тоді дві останні цифри у сумі повинні давати 14. Таких комбінацій усього: 95, 86, 68 та 59. Тут не пишемо комбінацію 77, бо тоді маємо число 777777, яке вже враховане у першому випадку.
Таким чином усього таких чисел  .
.
4. Для трикутника  позначимо через
позначимо через 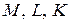 середини його сторін. Всередині
середини його сторін. Всередині 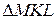 вибрана точка
вибрана точка  . Точки
. Точки  – симетричні відповідно точкам
– симетричні відповідно точкам  відносно точки
відносно точки  . Доведіть, що площа шестикутника
. Доведіть, що площа шестикутника  удвічі більша за площу
удвічі більша за площу  .
.
Розв’язання. Гомотетія  (рис. 9), тому
(рис. 9), тому 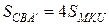 . Аналогічно
. Аналогічно  ,
,  . Разом маємо:
. Разом маємо:


 .
.
5. Чи існує таке натуральне число  , що його цифри можна переставити таким чином, що утвориться число
, що його цифри можна переставити таким чином, що утвориться число 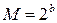 , для деякого
, для деякого 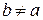 .
.
Відповідь: не існує.
Розв’язання. Припустимо, що це не так і існують такі значення  , для яких
, для яких 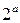 та
та  записані однаковими цифрами. Тому вони дають однакову остачу при діленні на 9. Тобто маємо, що
записані однаковими цифрами. Тому вони дають однакову остачу при діленні на 9. Тобто маємо, що
 або
або  .
.
Але найменша степінь числа 2, яка має таку властивість – це  , таким чином
, таким чином 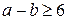 , звідки
, звідки  , тобто числа
, тобто числа 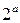 та
та  мають різну кількість цифр. Одержана суперечність завершує доведення.
мають різну кількість цифр. Одержана суперечність завершує доведення.
11 клас
1. Чи може  бути кутом трикутника, якщо він задовольняє рівність:
бути кутом трикутника, якщо він задовольняє рівність:  .
.
Відповідь: не може.
Розв’язання. Знайдемо можливі значення  із заданого рівняння:
із заданого рівняння:
 .
.
Тоді можливі варіанти:
 або
або  і найменше натуральне значення, що задовольняє таку рівність є
і найменше натуральне значення, що задовольняє таку рівність є  , що неможливо для кута трикутника.
, що неможливо для кута трикутника.
 або
або 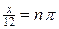 і найменше натуральне значення, що задовольняє таку рівність є
і найменше натуральне значення, що задовольняє таку рівність є  , що також неможливо для кута трикутника.
, що також неможливо для кута трикутника.
2. Чи існує таке натуральне число  , для яких обидва числа
, для яких обидва числа  та
та  є цілими?
є цілими?
Відповідь: такого натурального числа не існує.
Розв’язання. Припустимо методом від супротивного, що таке  існує, тоді позначимо одержані цілі числа як
існує, тоді позначимо одержані цілі числа як  та
та  , тоді
, тоді  з першої рівності, та
з першої рівності, та  з другої. Тоді
з другої. Тоді 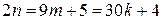 або
або  , що суперечить подільності на
, що суперечить подільності на  .
.
3. З множини  вибрали 5 різних чисел, з множини
вибрали 5 різних чисел, з множини  також вибрали 5 різних чисел. Виявилось, що різниця жодних двох чисел з десяти вибраних не кратна 10. Знайдіть суму усіх 10 вибраних чисел.
також вибрали 5 різних чисел. Виявилось, що різниця жодних двох чисел з десяти вибраних не кратна 10. Знайдіть суму усіх 10 вибраних чисел.
Відповідь: 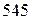 .
.
Розв’язання. Зумов задачі випливає, що в усіх обраних чисел різні останні цифри. Тому суму можна знайти, якщо окремо додати десятки та одиниці цих чисел. Серед десятків є п’ять по  та ще п’ять по
та ще п’ять по  , тому сума десятків дорівнює
, тому сума десятків дорівнює  . А серед одиниць маємо кожну цифра рівно один раз, тому їх сума дорівнює:
. А серед одиниць маємо кожну цифра рівно один раз, тому їх сума дорівнює: 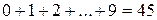 . Таким чином сума усіх десяти чисел дорівнює
. Таким чином сума усіх десяти чисел дорівнює 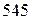 .
.
4. Для функції  справджується умова
справджується умова  . Доведіть, що вона має два нулі.
. Доведіть, що вона має два нулі.
Розв’язання. З умови задачі очевидно, що 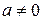 . Тепер умову задачі перепишемо таким чином:
. Тепер умову задачі перепишемо таким чином:
 або
або 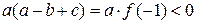 .
.
Тепер, якщо  , тобто гілки параболи направлені вгору, то
, тобто гілки параболи направлені вгору, то  і парабола має 2 нулі, аналогічно при
і парабола має 2 нулі, аналогічно при  .
.
5. Діагоналі 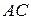 та
та  опуклого чотирикутника
опуклого чотирикутника  перпендикулярні та перетинаються в точці
перпендикулярні та перетинаються в точці  . Кола
. Кола  з центрами в точках
з центрами в точках  та радіусами
та радіусами  вписані у трикутники
вписані у трикутники  ,
,  ,
, 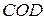 ,
, 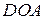 відповідно. Доведіть твердження:
відповідно. Доведіть твердження:
а)  ;
;
б)  .
.
Розв’язання. а) Використаємо відому формулу для радіуса вписаного кола для прямокутного трикутника з катетами  та гіпотенузою
та гіпотенузою  :
:  (рис. 10).
(рис. 10).



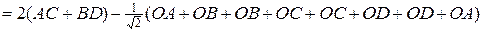
 .
.
б) З теореми Піфагора маємо, що 

 ,
,
останній перехід використовує пункт а).







