Ряды динамики широко применяются в статистике. Ряд нужно часто преобразовывать. Когда месячные данные заменяют квартальными или годовыми – это укрупнение ряда динамики.
Применение скользящей средней.
Январь – 3 преступления.
Февраль – 7 преступлений.
Март – 2 преступления.
Апрель – 10 преступления.
Май – 11 преступлений.
Июнь – 7 преступлений.
Берем янв, фев, март – средняя – 4.
Фев, март, апр – 6,3
Март апрель май – 7,6
Апрель май июнь – 9,3
Т.е. вместо динамического ряда мы получили ряд из скользящих средних: 4; 6,3; 7,6; 9,3.
Смыкание рядов динамики.
2001 – 6
2002 – 8 затем произошло изменение границ территории.
- 20
2003 - 22
20/8=2,5 – коэффициент соотношения данных по новой территории по отношению к старой.
6х2,5=15
ТО:
2001 – 15
2002 – 20
2003 - 22
Тема 6.
Выборочное исследование.
В ряде учебников м найти таблицы. В одной мы ищем предельную ошибку. В другой – размер выборки.
Тема 7. Функциональная связь процессов и явлений.
30.
В природе и обществе многие явления связанны между собой. Эта связь м б функциональной, когда за изменением одной переменной величины следует изменение другой.
В статистике эта связь называется корреляционной или статистической. Корреляционная связь – при изучении общественных явлениях.
Употребление алкоголя на душу населения по регионам – х
Совершение хулиганских – на 100 000 - у
Х у
3,5
4,5
5,5
6,5
Списать!!! Ибо с доски не видно, а что говорит – не слышно.
С изменением х на сколько изменится у – измерить корреляцию.
Надо высчитать сумму Х.
Сумма Х = 35.
Сумма У = 630.
Средняя Х – 5.
Средняя У – 90.
Х-Хсредняя
3,5-5=-1,5
-1
-0,5
+0,5
+1
+1,5
У-Усредняя.
87-90=-3
-2
-1
+1
+2
+3
Имеется формула коэффициента корреляции.

СПИСАТЬ ФОРМУЛУ!!!
Квадраты.
(Х-Хсредняя)2=dx2
2,25
1,0
2,5
2,5
1,0
2,25
(У-Усредняя)2=dу2
Сумма dx2 = 11,5
Сумма dy2 = 28
Списать!
Сумма Дх х на сумму Ду = 14.

Итак, коэффициент корреляции = 0,79.
Коэффициент корреляции м б от +-1 до 0. Если 0 – то корреляции (связи) нет. 0,3 – слабая. От 0,7 до 1 – сильная. 1 – почти функциональная связь.
Корреляция м б прямой и обратной.
Коэффициент ассоциации 4х полей.
Признаки
Группы
| Признаки Группы | ||
Списать!!!
| Причины наезда на пешехода | Вина водителей | Вина пешехода |
| Погибло | ||
| Ранено |
АД-БС/Корень(А+Б)х(С+Д)х(А+С)х(С+Д).
Данные и ссылки.
| Преступность Ульяновской области | 2008/2009 год | |
| Зарегистрировано преступлений | 22 425 / 21 056) | |
| ( | ||
| (-6,1%) | ||
| В т.ч. с участием несовершеннолетних | (-12,7%) | |
| В т.ч. тяжких и особо тяжких | (-2,6%) | |
| Удельный вес расследлованных | 55,3 | |
| Убийства | -29,6% | |
| Уд вес расследованных убийств | 89,5% | |
| Умышленное преступление тяжкого вреда здоровью | -14,8% | |
| Изнасилования | -27,5% | |
| Кража имущества | -11,9% | |
| ??? | -53% | |
| ПОЭП??? | +5,9% | |
| Данные взяты в информационно-аналитической бюллетени прокуратуры УО №1 за 2010 год стр. 205-206 | ||
| На 1 января 2010 года в исправительных учреждениях и СИЗО УО содержалось под стражей и надзором 11478 человек. – стр. 121 | В 2008 году нашли 1364 укрытых преступлений. 2009 году – 1322. Стр. 207. | |
| По данным Интернета, сайт госкомстат, в РФ всего было зарегистрировано преступлений в 2009 году | 2 594 820 | |
| 2 628 799 | ||
Лабораторная 1.
Статистика изучает какие-то совокупности. Полученные данные излагаются в рядах распределения. Ряды распределения бывают:
1) качественные (атрибутивные, типологические) – пример – мужчины-женщины;
2) количественные (вариационные) – пример, распределение по возрасту, по срокам лишения свободы. Вариационные ряды распределения м б:
а. дискретными (состоят только из целых чисел (возраст));
б. непрерывными (срок лишения свободы).
Вариационный ряд распределения состоит из вариант («Х») и частот, вес («t»).
Мода – это варианта, у которой наибольший вес.
Часто в статистике наряду с рядами распределения дают графическое выражение. Оно м б в виде диаграмм, картодиаграмм, картограмм. Диаграмма состоит из оси ординат и оси абсцисс. На оси абсцисс откладываются равные промежутки.
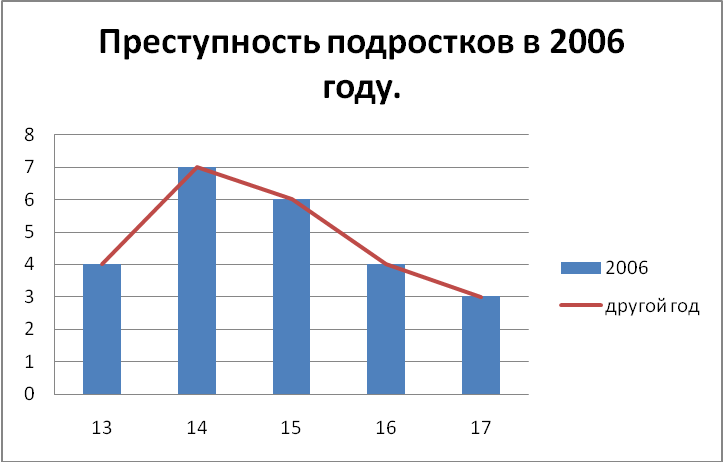
Задание 1. Органами МВД зарегистрирована подростковая преступность за май 2006 года в возрасте: 16, 13, 15, 13, 15, 17, 17, 15, 15, 14, 16, 14, 14, 14, 14, 14, 13, 16, 17, 16, 13, 15, 14, 15 лет. На основе этих данных:
- составить дискретный ряд распределения;
- произвести сравнительный анализ, если известно, что за аналогичный период 2005 года, преступления, совершенные подростками, распределились следующим образом:
| Возраст | Всего | |||||
| Число преступлений в процентах к итогу |
Число преступлений процентов к итогу 12 22 30 28 8 100
- постройте полигон-распределение, найти модальную величину ряда распределения, сделать вывод.
Решение.
Построить дискретный ряд-распределение, где верхняя строка – возраст, средняя – число преступлений, нижняя – число преступлений в процентах к итогу.
| Х | Всего | |||||
| F | ||||||
| T | 16,7 | 29,2 | 16,7 | 12,5 |
Преступность 13-них возросла, 14-них – возросла, 15 – снизилась, 16 – снизилась, 17 – возросла.
Мода – 7 – 14 лет. 14 лет – модальный возраст, модальная варианта.
Построение полигона.
Абсцисс – возраст
Преступление – ордината в масштабе.
Лабораторная 2.
При проведении плановых мероприятий по выявлению нарушений скоростного режима на автомобильных дорогах района зарегистрирована следующая скорость движения автотранспорта (км/ч): 168,115,137,124,145,105,135,125,122,146,170,135, 100,132,150,110,105,127,118,112,130,155,138,128, 142,100,130,150,135,180,120,145,125,140,175,140, 148,138,105,140.
Для анализа информации требуется:
- построить интервальный ряд распределения, образовав 4 группы с равными интервалами;
- изобразить полученный ряд распределения на графике.
Решение.
Х t
(100-120включительно) – 10;
(>120-140включительно) – 18;
(>141-160включительно) – 8;
(>160-180включительно) – 4.

Наибольшее количество машин проезжало со скоростью 120-140 км/ч. С наименьшей скоростью – 100-120 км/ч проехало 10 машин. С наивысшей скоростью – 160-180 км/ч проехало наименьшее количество машин – 4.
Интервальный вариационный ряд - такой ряд, когда варианты взяты в интервалах. При этом, интервалы м б равными и неравными.
Задание 3.
На основании приведенных в задании 2 данных и построенного вариационного ряда определите:
1. Среднюю скорость автомобилей, превысивших скорость:
а) на основе индивидуальных данных;
б) на основе построенного вариационного ряда.
2. Среднеквадратическое отклонение.
3. Коэффициент вариации.
4. Произведите выбор более точного значения средней скорости из перечисленных в п. 1 и обоснуйте его.
Решение.
1. Сложить все скорости и разделить на общее количество.
2. На основе вариационного ряда. Написать ряд.
Х t
(100-120включительно) – 10; 110 -10
(>120-140включительно) – 18; 130 -18
(>141-160включительно) – 8; 150 - 8
(>160-180включительно) – 4. 170 - 4
Хсредн= 110х10+130х18+150х8+170х4/10+18+8+4=?
3. Какая скорость более точная? Ответ: первая.
4.
Задание 4.
На основании следующей информации о стаже сотрудников РУВД:
| Стаж, лет | До 3 | 3–6 | 6–9 | 9–12 | 12–15 | 15 и более |
| Число работников |
определите:
1. Средний стаж сотрудников РУВД.
2. Модальный и медианный стаж сотрудников РУВД.
3. Изобразите приведенный вариационный ряд графически и сделайте выводы.
Лаба 5.
Для выявления причин роста преступности в регионе было проведено 5-процентное выборочное обследование. При механическом способе отбора в выборку попали следующие данные о возрасте преступников:
| Возраст, лет X | До 16 | 16–20 | 20–24 | 24–28 | 28 и более | Итого |
| Число совершенных Преступлений F |
Определите:
1. С вероятностью 0,997 возможные пределы доли преступников в возрасте до 16 лет.
2. С вероятностью 0,954 возможные пределы среднего возраста преступников.
Часто применяется выборочное исследование. При выборочном исследовании мы имеем генеральную совокупность и выборочную совокупность. Выборка должна обеспечивать нормальные выводы.
Возраст – варианты x, число преступлений – вес, частота вариант – t f.
Это вариационный ряд распределения, интервальный ряд,
n – количество преступлений по выборке = 250.
N – 5000 – количество преступлений генеральной совокупности.
250 преступлений – 5%
Х преступлений – 100%
Х=250х100/5=5000
1) Найти долю преступников до 16 лет.
Удельный вес преступлений до 16 лет вычисляем так:
250 = 100%
35 преступлений = Х%
Х=35х100/250=14%- 0,14
Доля до 16 лет – 0,14 в общей массе преступлений.
Р -0,14 или 14%
t – коэффициент доверия = 3.
См на листке.
Каковы возможные пределы доли преступников до 16 лет.
0,14 + 0,06
От 0,2 до 0,08 – от 20% до 8%.
2) Возможные пределы среднего возраста преступников.
Cм рисунок
Коэффициент доверия = 2.
Для того, чтобы определить дисперсию проделаем следующие действия.
| Возраст, лет X | До 16 | 16–20 | 20–24 | 24–28 | 28 и 32 | Итого |
| Число совершенных Преступлений F |
Хсредняя арифметическая взвешенная = суммаХхF/суммуF
15 18 22 26 30
15х35+18х72+22х68+26х51+30х24/250=21,85 – средний возраст преступников.
G2
Cм рисунок
+ 0,56
От 21,29 до 22,41.
Учебник по статистике Лунеева 127, 137, 130
Учебник Савюка.
Задание 6.
Для определения среднего возраста 50 тыс. человек, совершивших экономические преступления в РФ, необходимо провести выборочное обследование методом механического отбора. При проведении предыдущего подобного обследования величина дисперсии составила 75. Определите необходимую численность выборки, чтобы с вероятностью 0,997 предельная ошибка выборки не превышала бы 2,5 года.
Задание 7.
По данным МВД, число экономических преступлений в регионе в 2003–2007 гг. составило (см. нижеприводимую таблицу). В 2004 г. произошло укрупнение региона.
По приведенным данным:
| Число преступлений | |||||
| В прежних границах региона | |||||
| В новых границах региона |
1. Укажите вид ряда динамики.
2. Произведите смыкание рядов динамики.
3. Проведение анализ динамики числа экономических преступлений в регионе за 2003–2007 гг. на основе абсолютных, относительных и средних показателей динамики.
4. Изобразите графически интенсивность динамики и сделайте выводы.
5. Сделайте прогноз числа экономических преступлений в регионе на 2008 г.
Задание 8.
По данным МВД, в январе 2006 г. выявлено следующее количество лиц, совершивших преступления (в тыс. чел.):
| До 30 лет | Старше 30 лет | Итого | |
| Мужчины | 71,7 | 34,8 | 106,5 |
| Женщины | 7,3 | 12,2 | 20,5 |
| Итого | 79,0 | 48,0 | 127,0 |
Для оценки связи между полом и возрастом определите коэффициент ассоциации и сделайте вывод.






