Работа 3. ИССЛЕДОВАНИЕ ПРОЦЕССА ИСТЕЧЕНИЯ ВОЗДУХА
ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО
1. Цель работы. Исследование зависимости массового расхода воздуха через суживающееся сопло от отношения давления за соплом к давлению перед соплом.
2. Основные положения. Канал, в котором с уменьшением давления скорость газового потока возрастает, называется соплом; канал, в котором скорость газа уменьшается, а давление возрастает, называется диффузором. Поскольку назначением сопла является преобразование потенциальной энергии рабочего тела в кинетическую, для анализа происходящего в нем процесса начальная скорость потока является несущественной, и можно принять W1 = 0. Тогда уравнение первого закона термодинамики при адиабатном истечении рабочего тела через сопло принимает вид:
, (1)
где W0 —теоретическая скорость потока в выходном сечении сопла;
Р1 — начальное давление рабочего тела;
Р2 — давление среды, в которую происходит истечение.
Разность энтальпий (h1 – h2) при истечении через сопла также называется располагаемым теплопадением и обозначается через h0. Она соответствует тому максимуму кинетической энергии, который может быть получен лишь в идеальных условиях истечения, а фактически из-за неизбежных потерь, связанных с необратимостью процесса, никогда не достигается.
Исходя из равенства W02/2 = h0, теоретическую скорость истечения рабочего тела через сопло в рассматриваемом случае можно определить по формуле:
, м/сек (2)
Здесь h0 выражено в кДж/кг. Это соотношение справедливо для любого рабочего тела.
Рассмотрим адиабатное истечение газа через суживающееся сопло из резервуара (рис.1) достаточно большого объема, в котором изменением давления можно пренебречь (Р1 ≈ const).
В резервуаре газ имеет параметры Р1, T1, v1 (ρ1), а на выходе из сопла Р2, Т2, v2 (ρ1), W2. Давление среды, в которую происходит истечение газа, обозначим Р0. Основной характеристикой процесса истечения является отношение конечного давления к начальному, т. е. величина β= Р0/Р1.
В зависимости от отношения давлений можно выделить три характерных режима истечения газа: при β>βкр − докритический, при β = βкр − критический и при β<βкр− сверхкритический режимы.
Значение β, при котором расход газа достигает максимума, называется критическим βкр, и находится по формуле:
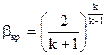, (3)
Как и показатель адиабаты, величина βкр является физической константой газа, т. е. одной из характеристик его физических свойств.
При докритическом режиме истечения (β>βкр) в сопле происходит полное расширение газа с понижением давления от Р1 до Р0, на срезе сопла Р2 = Р0, скорость на выходе меньше скорости звука (рис. 2,а), располагаемая работа, соответствующая площади 1'-1-2-2'-1', полностью расходуется на увеличение кинетической энергии газа. При критическом режиме (β = βкр) также происходит полное расширение газа в пределах сопла, на срезе сопла Р2 = Ркр = Р1·βкр = Р0, скорость на выходе равна критической скорости – скорости звука (рис. 2,б), располагаемая работа полностью расходуется на увеличение кинетической энергии газа. При сверхкритическом режиме (β<βкр) в пределах сопла происходит неполное расширение газа, давление понижается только до критического, на срезе сопла Р2=Ркр=Ρ1·βкр>Ρ0, скорость на выходе равна критической скорости – местной скорости звука (рис.2, в). Дальнейшее расширение газа и понижение его давления до Р0 осуществляется за пределами сопла. На увеличение кинетической энергии расходуется только часть располагаемой работы, соответствующая площади 1'-1-2-2'-1', другая ее часть, соответствующая площади 2'-2-20 -20'-2', в суживающемся сопле остается не реализуемой.
 |
Скорость газа на выходе из суживающегося сопла определяется по формулам:
для первого случая, когда β>βкр Р2 = Р0:
, (4)
для второго и в третьего случаев, когда β = βкр, а Р2 = Ркр = Р1·βкр = Р0 и β<βкр, а Р2=Ркр=Ρ1·βкр>Ρ0
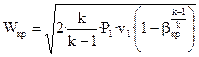, (5)
или, подставив значение βкр из формулы (3), получим:
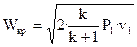, (6)
тогда при условиях адиабатного истечения
, (7)
Полученная формула показывает, что критическая скорость истечения газа из сопла равна скорости распространения звуковой волны в этом газе при его параметрах Ркр и vкр, т е местной скорости звука С в выходном сечении сопла.
В этом содержится физическое объяснение тому, что при снижении внешнего давления Р0ниже Ркр скорость истечения не изменяется, а остается равной Wкр.
Действительно, если Р0>Ркр, то W0<Wкрили W0<C, то всякое понижение давления Р0 передается вдоль сопла в направлении, обратном движению потока, со скоростью(C − W0) > 0. При этом происходит перераспределение давления и скоростей по всей длине сопла· в каждом промежуточном сечении устанавливается новая скорость, соответствующая большему расходу газа. Если же Р0снизится до Ркр, то дальнейшее понижение его уже не сможет распространяться вдоль сопла, поскольку скорость его распространения навстречу потоку снизится до нуля (C − Wкр) = 0. Поэтому в промежуточных сечениях сопла расход газа не изменится, не изменится он и в выходном сечении, т е скорость истечения останется постоянной и равной Wкр.
Зависимость скорости и расхода газа на выходе из суживающегося сопла от отношения давлений β = Р0/Р1 показана на рис. 3. Экспериментально эта зависимость была получена А.Сен-Венаном в 1839 году.
В отличие от теоретического изоэнтропийного действительный процесс истечения реального газа происходит при трении частиц газа между собой и о стенки канала. При этом работа, затрачиваемая на преодоление сил трения, преобразуется в теплоту, в результате чего температура и энтальпия газа в выходном сечении канала возрастают.
Истечение газа с трением становится необратимым процессом и сопровождается увеличением энтропии.
На рис. 4 в sh - координатах представлены процессы расширения газа 1-2 при истечении без трения и 1-2 д при истечении с трением. При одинаковом перепаде давлений Р1 − Р2 действительный теплоперепад Δh д = h1-h2 д меньше располагаемого Δh = h1 − h2. В результате этого действительная скорость истечения газа оказывается меньше теоретической.
Отношение разности располагаемого и действительного теплоперепадов (потери теплоперепада) к располагаемому теплоперепаду называется коэффициентом потери энергии
ζс = (Δh − Δh д)/Δh (8)
Отсюда
Δh д = (1 − ζс)·Δh (9)
Коэффициентом потери скорости называется отношение действительной скорости истечения к теоретической
, (10)
Коэффициент потери скорости, учитывающий уменьшение действительной скорости по сравнению с теоретической, в современных соплах равен 0,95 - 0,98.
Отношение действительного теплоперепада Δh д к теоретическому
Δh, или действительной кинетической энергии W д 2/2 к теоретической W2/2 называется коэффициентом полезного действия канала
, (11)
С учетом выражений (8) и (10)
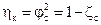, (12)
3. Схема и описание установки. Воздух от ресивера поршневого компрессора (на схеме не показан) (рис. 5) по трубопроводу поступает через измерительную диафрагму 1 к суживающемуся соплу 2. В камере 3 за соплом, куда происходит истечение, можно устанавливать различные давления выше барометрического путем изменения проходного сечения для воздуха с помощью вентиля 5. А затем воздух направляется в атмосферу. Сопло выполнено с плавным сужением. Диаметр выходного сечения сопла 2,15 мм. Суживающийся участок сопла заканчивается коротким цилиндрическим участком с отверстием для отбора и регистрации давления Р2м′ и температуры t2 д в выходном сечении сопла (прибор 12).. Измерительная диафрагма 1 представляет собой тонкий диск с круглым отверстием по центру и вместе с дифманометром 7 служит для измерения расхода воздуха.
Температура и давление воздуха в окружающей среде измеряются соответственно термометром 8 и чашечным ртутным барометром 6.
 | |||
 | |||
Температура и давление воздуха перед измерительной диафрагмой замеряется с помощью комбинированного прибора 9, а перед соплом − прибором 10. Давление за соплом измеряется манометрической частью комбинированного прибора 11. Все показания приборов заносятся в протокол наблюю дений (таблица 1).
Таблица 1.
| № п/п | Измеряемая величина | Обозна- чение | Единицы измерен. | Номера опытов | ||||||||||
| Показание манометра перед диафрагмой | Рм | ати | ||||||||||||
| Показание манометра перед соплом | Р1м | ати | ||||||||||||
| Показание манометра в выходном сечении сопла | Р2м' | ати | ||||||||||||
| Показание манометра за соплом | Р2м | ати | ||||||||||||
| Показания дифманометра | H | мм вод.ст. | ||||||||||||
| Температура перед диафрагмой | t | °С | ||||||||||||
| Температура перед соплом | t1 | °С | ||||||||||||
| Температура в выходном сечении сопла | t2 д | °С | ||||||||||||
| Температура окружающей среды | tв | °С | ||||||||||||
| Показания барометра | B | мбар |
4. Расчетные формулы и расчеты.
4.1. Атмосферное давление находится с учетом температурного расширения столбика ртути барометра по формуле
, Па (13)
4.2. Перевод показаний образцовых манометров Рм, Р1м, Р2м' и Р2м в абсолютные значения давлений по формуле
, Па (14)
где g − ускорение свободного падения, равное 9,81 м/сек2;
Рмj − показания одного из четырех манометров из табл. 1.
4.3. Перепад давления воздуха на диафрагме
, Па (15)
где ρ – плотность воды в U-образном вакуумметре, равная 1000 кг/м3;
Н – показание дифманометра, переведенное в м вод.ст.
4.4. Плотность воздуха по состоянию перед диафрагмой:
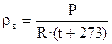, кг/м3 (16)
где R – характеристическая газовая постоянная воздуха, равная 287 Дж/кг·°К.
4.5. Действительный расход воздуха через диафрагму (следовательно, через сопло):
, кг/сек (17)
4.6. Теоретическая скорость истечения в выходном сечении сопла:
, м/сек (18)
4.7. Значения энтальпий воздуха h1 и h2 в сечениях на входе и на выходе из сопла определяется по общему уравнению:
, кДж/кг (19)
где ср – теплоемкость воздуха при постоянном давлении, которая может быть принята не зависящей от температуры и равной 1,006 кДж/(кг·°С);
tj – температура в рассматриваемом сечении, °С;
j – индекс рассматриваемого сечения.
4.8. Теоретическое значение температуры в выходном сечении сопла находится из условия адиабатного процесса истечения по формуле:
, °К, а t2 = T2 − 273, °C (20)
где β – значение отношения давлений. Величину β принимают по данным таблицы результатов расчета (таблица 2) для конкретного опыта, когда режим истечения докритический, т.е. β > βкр; для всех остальных опытов, когда β = βкр − критический и β < βкр− сверхкритический режимы, величина β в формуле (20) равна βкр (независимо от данных таблицы 2) и находится по уравнению (3) при k = 1,4.
4.9. Действительный процесс истечения сопровождается увеличением энтропии и температуры Т2 д (рис. 4).Действительная скорость истечения при этом также уменьшается и может быть найдена по уравнению
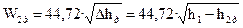, м/сек (21)
4.10. Коэффициент потери энергии находится по формуле (8).
4.11. Коэффициент потери скорости находится по формуле (10).
4.12. Коэффициент полезного действия канала рассчитывается по формуле (11) или (12).
4.13. Результаты расчетов должны быть продублированы в форме сводной таблицы 2.
Таблица 2.
| № п/п | Измеряемая величина | Обозна- чение | Единицы измерен. | Номера опытов | ||||||||||
| Давление перед диафрагмой | Р | Па | ||||||||||||
| Давление перед соплом | Р1 | Па | ||||||||||||
| Давление в выходном сечении сопла | Р2' | Па | ||||||||||||
| Давление за соплом | Р2 | Па | ||||||||||||
| Отношение давлений | β | − | ||||||||||||
| Перепад давления на диафрагме | ΔР | Па | ||||||||||||
| Плотность воздуха перед диафрагмой | ρ | кг/м3 | ||||||||||||
| Действительный расход воздуха (с точностью до трех значащих цифр) | Gд | кг/сек | ||||||||||||
| Теоретическая температура в выходном сечении сопла | Т2 | °К | ||||||||||||
| Действительная температура в выходном сечении сопла | Т2 д | °К | ||||||||||||
| Теоретическая скорость истечения | W2 | м/сек | ||||||||||||
| Действительная скорость истечения | W2 д | м/сек | ||||||||||||
| Коэффициент потери энергии | ζс | − | ||||||||||||
| Коэффициент потери скорости | φc | − | ||||||||||||
| Коэффициент полезного действия канала | ηк | − |
4.14. По результатам расчетов построить в соответствующем масштабе график зависимости расхода газа от отношения давлений.
5. Контрольные вопросы.
5.1. Сформулируйте цель лабораторной работы и поясните, как достигается поставленная цель?
5.2. Назовите основные узлы экспериментальной установки и укажите их назначение.
5.3. Дайте определение процессов истечения и дросселирования.
5.4. Напишите уравнение первого закона термодинамики применительно к процессу истечения.
5.5. Напишите уравнение первого закона термодинамики применительно к процессу дросселирования.
5.6. Как изменяется скорость истечения через суживающееся сопло при изменении β от 1 до 0 (покажите качественное изменение на графике расхода)?
5.7. Чем объясняется проявление критического режима при истечении?
5.8. В чем различие теоретического и действительного процессов истечения?
5.9. Как изображается теоретический и действительный процессы истечения в координатах h-s?
5.10. Почему отличаются теоретическая и действительная температуры воздуха на выходе из сопла при истечении?
5.11. На каком основании процесс дросселирования используется при измерении расхода воздуха?
5.12. Как может изменяться температура воздуха в процессе дросселирования?
5.13. От чего зависят величины коэффициентов: потери скорости φс, потери энергии ζс и полезного действия канала ηк?
5.14. Какие каналы называются соплами?
5.15. От каких параметров зависят расход и скорость газа при истечении через сопло?
5.16. Почему температуры воздуха перед диафрагмой и перед соплом равны?
5.17. Как изменяются энтальпия и энтропия потока газа, при прохождении через диафрагму?
Работа 4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТЕПЛОИЗОЛЯЦИОННОГО МАТЕРИАЛА (метод цилиндрического слоя).
1. Цель работы. Освоение одного из методов определения коэффициента теплопроводности теплоизоляционных материалов (метод цилиндрического слоя) и закрепление знаний по теории теплопроводности.
2. Основные положения. Теплота является наиболее универсальной формой передачи энергии, возникающей в результате молекулярно-кинетического (теплового) движения микрочастиц - молекул, атомов, электронов. Универсальность тепловой энергии состоит в том, что любая форма энергии (механическая, химическая, электрическая, ядерная и т.п.) трансформируется, в конечном счете, либо частично, либо полностью в тепловое движение молекул (теплоту). Различные тела могут обмениваться внутренней энергией в форме теплоты, что количественно выражается первым законом термодинамики.
Теплообмен − это самопроизвольный процесс переноса теплоты в пространстве с неоднородным температурным полем.
Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства. Поскольку температура − скалярная величина, то температурное поле − скалярное поле.
В общем случае перенос теплоты может вызываться неоднородностью полей других физических величин (например, диффузионный перенос теплоты за счет разности концентраций и др.). В зависимости от характера теплового движения различают следующие виды теплообмена.
Теплопроводность - молекулярный перенос теплоты в среде с неоднородным распределением температуры посредством теплового движения микрочастиц.
Конвекция − перенос теплоты в среде с неоднородным распределением температуры при движении среды.
Теплообмен излучением − теплообмен, включающий переход внутренней энергии тела (вещества) в энергию излучения, перенос излучения, преобразование энергии излучения во внутреннюю энергию другого тела (вещества).
В зависимости от времени теплообмен может быть:
стационарным, если температурное поле не зависит от времени;
нестационарным, если температурное поле меняется во времени.
Для количественного описания процесса теплообмена используют следующие величины:
Температура Т в данной точке тела, осредненная: по поверхности, по объему, по массе тела. Если соединить точки температурного поля с одинаковой температурой, то получим изотермическую поверхность. При пересечении изотермической поверхности плоскостью получим на этой плоскости семейство изотерм − линий постоянной температуры.
Перепад температур ΔΤ − разность температур между двумя точками одного тела, двумя изотермическими поверхностями, поверхностью и окружающей средой, двумя телами. Перепад температуры вдоль изотермы равен нулю. Наибольший перепад температуры происходит по направлению нормали к изотермической поверхности. Возрастание температуры по нормали к изотермической поверхности характеризуется градиентом температуры.
Средний градиент температуры 
− отношение перепада температур между двумя изотермическими поверхностями ΔΤ к расстоянию между ними Δn, измеренному по нормали n к этим поверхностям (рис. 1).
Истинный градиент температуры 
− средний градиент температуры при Δn—>0 или это есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры, численно равный первой производной температуры по этой нормали.:
, (1)
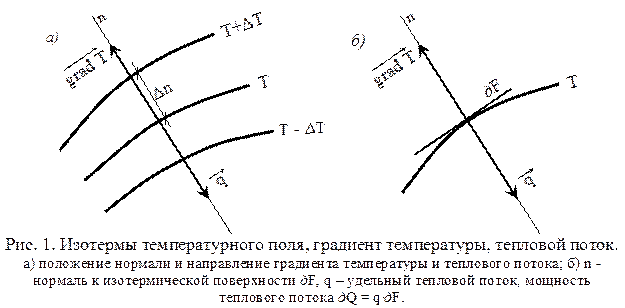
Количество теплоты − д Q, Дж, мощность теплового потока 
, Вт − количество теплоты, проходящее в единицу времени, удельный тепловой поток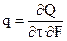 
, Вт/м2 – количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности.
Перенос теплоты теплопроводностью выражается эмпирическим законом Био-Фурье, согласно которому вектор удельного теплового потока прямо пропорционален градиенту температуры:
. (2)
Знак «минус» в уравнении (2) показывает, что направление теплового потока противоположно направлению градиента температуры.
Коэффициент пропорциональности λ в уравнении (2) характеризует способность тел проводить теплоту и называется коэффициентом теплопроводности. Количественно коэффициент теплопроводности λ - тепловой поток (Вт), проходящий через единицу поверхности (м2) при единичном градиенте температур (град/м), и имеет размерность Вт/(м·град).
Коэффициент теплопроводности - физическая характеристика, зависящая от химического состава и физического строения вещества, его температуры, влажности и ряда других факторов. Коэффициент теплопроводности имеет максимальные значения для чистых металлов и минимальные для газов.
Теплоизоляционные материалы. К числу теплоизоляционных материалов могут быть отнесены все материалы, обладающие низким коэффициентом теплопроводности (менее 5 Вт/(м·град) при t = 0 °С).
Теплоизоляционные материалы могут быть неорганического происхождения (асбест, шлаки, глины, пески, минералы и т.д.), органического (шерсть, хлопок, дерево, кожа, резина, текстолит и т.д.) и смешанными, т.е. состоящими одновременно из органических и неорганических веществ. Материалы органического происхождения используют в области температур, не превышающих +150 ° С. Для более высоких температур применяются материалы неорганического происхождения.
Теплопроводность твердых теплоизоляционных материалов, как правило, определяется их пористостью (т.е. общим объемом газовых включений, отнесенным к единице объема изоляционного материала), размером пор и влажностью. С ростом влажности теплопроводность увеличивается. Теплопроводность пористых тел сильно возрастает с температурой; при температурах более 1300°С тепловые изоляторы становятся проводниками тепла. Сплошные диэлектрические материалы, например стекло, имеют более высокую теплопроводность по сравнению с пористыми материалами.
Установлено также, что чем выше плотность материала, тем больше его теплопроводность.
Однослойная стенка (трубка) при λ = const. Рассмотрим цилиндрическую стенку (трубку) длиной l с внутренним r1 и внешним r2 радиусами (рис. 2).
Заданы температуры T1 внутренней и T2 наружной поверхностей стенки. Условием одномерности теплового потока будет условие l >>> r2, откуда следует дq / дl = 0.
Дифференциальное уравнение теплопроводности в полярных координатах при λ=const и отсутствии внутреннего источника теплоты (Qv = 0) имеет вид:
. (3)
При заданных граничных условиях:
r = r1; T = T1;
r = r2; T = T2.
получим
. (4)
Согласно уравнению (4) температура цилиндрической стенки меняется по логарифмической зависимости (рис. 2).
Удельный тепловой поток q через единицу площади цилиндрической поверхности будет величиной переменной:
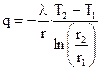. (5)
Мощность теплового потока Q=q·F через цилиндрическую поверхность площадью F=2π ·r· l (l - длина цилиндрической стенки) есть постоянная величина, равная:
. (6)
Формулу (6) можно записать, используя понятие термического сопротивления:
, (7)
где 
− термическое сопротивление цилиндрической стенки.
Удельный тепловой поток на единицу длины стенки q l = Q/ l:
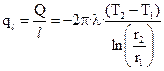. (8)
Таким образом, предлагаемый экспериментальный метод определения коэффициента теплопроводности основан на измерении:
· мощности теплового потока, проходящего через цилиндрический слой;
· перепада температур между внутренней и наружной поверхностями слоя тепловой изоляции;
· геометрических характеристик слоя тепловой изоляции.
 |
3. Схема и описание установки. Исследуемый материал 1 (рис. 3) нанесен в виде цилиндрического слоя (d1 = 0,05, м; d2 = 0,02, м) на наружную поверхность металлической трубы 2. Длина цилиндра тепловой изоляции составляет 1 м, что значительно больше наружного диаметра.
Источником теплового потока служит электронагреватель 3, который включен в электрическую цепь через автотрансформатор 4. Для определения мощности теплового потока служат вольтметр 5 и амперметр 6. Для измерения температур на внутренней и наружной поверхностях тепловой изоляции применяются хромель-копелевые термопары 7 и 8 в комплекте с вторичными приборами 9 и 10.
Результаты измерений при достижении стационарного режима заносятся в протокол наблюдений (табл. 1). Стационарность режима оценивается по неизменности температур t1 и t2 во времени.
Исследуемый материал................................ Таблица 1.
| № п/п | Измеряемая величина | Обозна- чение | Единицы измерен. | Номера опытов | ||||
| Сила тока | I | а | ||||||
| Напряжение | U | в | ||||||
| Температура внутренней поверхности слоя изоляции | t2 | °С | ||||||
| Температура наружной поверхности слоя изоляции | t1 | °С |
4. Расчетные формулы и расчеты.
4.1. Все расчеты сводятся к вычислениям коэффициента теплопроводности на основе выражения (6) по формуле:
, Вт/(м·град) (9)
4.2. Мощность теплового потока по формуле:
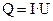, Вт (10)
4.3. Средняя температура тепловой изоляции:
, °С (11)
4.4. Результаты расчетов должны быть продублированы в форме сводной таблицы 2.
Исследуемый материал................................ Таблица 2.
| № п/п | Измеряемая величина | Обозна- чение | Единицы измерен. | Номера опытов | ||||
| Тепловой поток | Q | Вт | ||||||
| Средняя температура исследуемого материала | tcр | °С | ||||||
| Коэффициент теплопроводности исследуемого материала | l | Вт/ (м·град) | ||||||
| Температурный коэффициент | b | 1/град |
4.5. По результатам расчетов построить в соответствующем масштабе график зависимости коэффициента теплопроводности от средней температуры тепловой изоляции. Пользуясь графиком, определить коэффициент β, характеризующий влияние температуры на теплопроводность материала. При обработке графического материала характер зависимости представить в виде уравнения прямой линии:
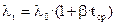. (12)
5. Контрольные вопросы.
5.1. Сформулируйте цель лабораторной работы и поясните, как достигается поставленная цель?
5.2. Назовите основные узлы экспериментальной установки и укажите их назначение.
5.3. Какие величины следует измерять в данной работе, чтобы вычислить коэффициент теплопроводности?
5.4. Какова физическая сущность передачи тепла теплопроводностью?
5.5. Сформулируйте понятия: температурное поле, изотермическая поверхность, градиент температуры, мощность теплового потока, удельный тепловой поток.
5.6. Покажите на схеме установки, как направлен вектор теплового потока и градиента температуры?
5.7. Каков физический смысл коэффициента теплопроводности, и от каких факторов он зависит?
5.8. Каков характер изменения температуры по толщине плоской и цилиндрической стенок?
5.9. Какова взаимосвязь между коэффициентом теплопроводности и наклоном температурной кривой по толщине тепловой изоляции?
5.10. Дайте определение понятию термического сопротивления стенки.
5.11. Как зависит коэффициент теплопроводности различных веществ (металлов, неметаллов, жидкостей и газов) от температуры? Ответ обосновать.
5.12. Сформулируйте основной закон теплопроводности. В чем его сущность?
5.13. Каковы основные трудности тепловых расчетов при переносе тепла теплопроводностью?
5.14. Как влияет форма стенки на величину её термического сопротивления?
