ЛАБОРАТОРНАЯ РАБОТА № 3
ПО ФИЗИКЕ
Выполнил студент Принял
1-го курса
доцент
Уч.шифр 13-ЗЭТ- Макоед И.И.
Брест 2014
ЛАБОРАТОРНАЯ РАБОТА № 3
ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ (2)
Ознакомьтесь с теорией в конспекте, учебнике (Савельев, т.1, §3, 4). Запустите программу Open Physics. Прочитайте краткие теоретические сведения по теме «Движение в поле силы тяжести». Необходимые данные запишите в свой конспект.
ЦЕЛЬ РАБОТЫ:
* Знакомство с применением физической модели МАТЕРИАЛЬНАЯ ТОЧКА (МТ).
* Исследование движения МТ с постоянным ускорением.
* Экспериментальное определение ускорения свободного падения на поверхности Земли.
КРАТКАЯ ТЕОРИЯ:
МАТЕРИАЛЬНАЯ ТОЧКА это абстрактный объект (модель), не имеющий размеров, но обладающий другими характеристиками реального тела.
ПОЛОЖЕНИЕ МТ это координата, которую имеет МТ в данный момент времени. Математическое описание положения МТ - ее радиус-вектор  .
.
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ есть изменение положения тела в пространстве со временем. Закон движения - это функция  .
.
СКОРОСТЬ есть векторная кинематическая характеристика движения, показывающая быстроту и направление движения. Математически  .
.
УСКОРЕНИЕ есть векторная кинематическая характеристика движения, показывающая быстроту и направление изменения скорости. Математически  .
.
ТРАЕКТОРИЯ есть геометрическое место точек, которые проходит МТ при ее движении. В каждой точке вектор скорости направлен по касательной к траектории.
Для движения с постоянным ускорением закон движения
 , где
, где  - начальное положение и
- начальное положение и  - начальная скорость МТ. Закон скорости:
- начальная скорость МТ. Закон скорости:  .
.
При свободном движении тела вблизи поверхности Земли  - ускорению свободного падения.
- ускорению свободного падения.
ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется величина скорости  ; оно направлено по касательной к траектории.
; оно направлено по касательной к траектории.
НОРМАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется направление вектора скорости  (R – радиус кривизны траектории). Оно перпендикулярно касательной.
(R – радиус кривизны траектории). Оно перпендикулярно касательной.
Полное ускорение определяется по теореме Пифагора: 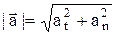 .
.
ЗАДАНИЕ: Выведите формулу для ymax максимальной высоты подъема тела (в черновике).
УКАЗАНИЯ: Для верхней точки траектории вертикальная проекция скорости равна нулю. Из уравнения  , выразите tДВ и подставьте в формулу для y(t).
, выразите tДВ и подставьте в формулу для y(t).
z:\Disc_E\Open Phys\design\images\buttonModel_h.gif

|
| Модель. Движение тела, брошенного под углом к горизонту |
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
Выключите “Стробоскоп”, установив маркер мыши на квадрат и нажав на левую кнопку мыши.
Нажмите мышью кнопку «СТАРТ». Внимательно рассмотрите картинку в средней части монитора. Найдите регуляторы с движками, задающие высоту y, начальную скорость V=V0 и угол бросания a. Подведите маркер мыши к движку регулятора высоты, нажмите и удерживайте левую кнопку мыши, двигая мышь вниз. Движок регулятора будет двигаться за маркером мыши. Доведите его до положения, соответствующего высоте y=h, указанной в табл.1 для вашей бригады. Тем же методом «зацепив мышью и двигая движок регулятора» или щелкая мышью по стрелке на движке, установите значения угла бросания, указанные в табл.1 (см. ниже) для вашей бригады.
Нажмите мышью кнопку «Старт» внизу экрана и, когда МТ будет в верхней точке траектории (вертикальная компонента скорости Vy должна быть мала), остановите движение кнопкой «Стоп» Запомните значение высоты, показанное справа. Для продолжения движения тела нужно нажать кнопку «Старт». Потренируйтесь, очищая экран (кнопка «Очистить» на экране), повторяя запуск (кнопка «Старт» на экране) и сравнивая полученные значения высоты.
Получите у преподавателя допуск для выполнения измерений.
Приступайте к измерениям на первой траектории, записывая результаты пяти измерений координаты ymax в таблицу 2, образец которой приведен ниже. Повторите измерения для четырех других траекторий, начальные параметры движения для которых указаны в таблицах 1 и 2.
Таблица 1. Начальные параметры траекторий (не перерисовывать)
| Номер бригады | Начальная высота h,(м) | Начальный угол a,(град) | Номер бригады | Начальная высота h,(м) | Начальный угол a,(град) |
Таблица 2. Результаты измерений
| Номер измерения | Траектор. 1 vo = 15 (м/с) | Траектор. 2 vo = 17 (м/с) | Траектор. 3 vo = 19 (м/с) | Траектор. 4 vo = 22 (м/с) | Траектор. 5 vo = 25 (м/с) | |||||
| ymax | Dymax | ymax | Dymax | ymax | Dymax | ymax | Dymax | ymax | Dymax | |
| 18.6 | 0.06 | 0.04 | 23.8 | 0.02 | 28.5 | 33.9 | ||||
| 18.5 | 0.04 | 0.04 | 23.7 | 0.08 | 28.5 | 33.9 | ||||
| 18.5 | 0.04 | 21.1 | 0.06 | 23.8 | 0.02 | 28.5 | 33.9 | |||
| 18.6 | 0.06 | 21.1 | 0.06 | 23.8 | 0.02 | 28.5 | 33.9 | |||
| 18.5 | 0.04 | 0.04 | 23.8 | 0.02 | 28.5 | 33.9 | ||||
| <ymax> | 18.54 | 21.04 | 23.78 | 28.5 | 33.9 | |||||
| Абс.ошибка <ymax> |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Вычислите и запишите в таблицу средние значения вертикальной координаты точки максимального подъема <ymax> и отклонения Dymax измеренного значения от среднего.
Постройте график зависимости средних значений вертикальной координаты точки максимального подъема <ymax> от квадрата начальной скорости.
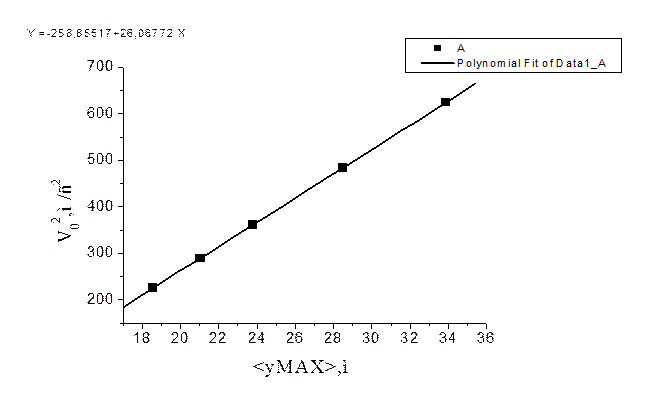
Определите по графику значение ускорения свободного падения g, используя формулу  .
.

Вычислите ошибку среднего значения g.
g=9.82 м/с;
gэксп=9.77 м/с;


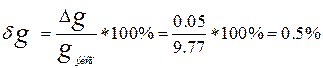
Запишите ответ и проанализируйте ответ и график.
Получили экспериментальную величину ускорения свободного падения, равную 9.77 м/с. Разница в экспериментальной и действительной величинах составляет 0.5%, что соответствует норме.
Вопросы и задания для самоконтроля по работе 3
1. Дайте определение материальной точки.
МАТЕРИАЛЬНАЯ ТОЧКА это абстрактный объект (модель), не имеющий размеров, но обладающий другими характеристиками реального тела.
2. Как определяется положение материальной точки?
ПОЛОЖЕНИЕ МТ это координата, которую имеет МТ в данный момент времени. Математическое описание положения МТ - ее радиус-вектор  .
.
3. Дайте определение системы отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
4. Что такое декартова система координат?
Декартовой называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат (не прямоугольную).
5. Дайте определение механического движения.
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ есть изменение положения тела в пространстве со временем. Закон движения - это функция  .
.
6. Что такое скорость материальной точки?
СКОРОСТЬ есть векторная кинематическая характеристика движения, показывающая быстроту и направление движения. Математически  .
.
7. Как математически записывается быстрота изменения какой либо переменной величины?
Быстрота изменения любой переменной величины есть производная этой величины по времени.
8. Дайте определение ускорения МТ?
УСКОРЕНИЕ есть векторная кинематическая характеристика движения, показывающая быстроту и направление изменения скорости. Математически  .
.
9. Что такое траектория движения МТ?
ТРАЕКТОРИЯ есть геометрическое место точек, которые проходит МТ при ее движении. В каждой точке вектор скорости направлен по касательной к траектории.
10. Что такое закон движения?
Закон движения – это уравнение, которое описывает движение материальной точки. Закон движения в векторной форме – зависимость радиус-вектора от скорости. Закон движения - это функция r (t) = { x(t), y(t), z(t) }.
11. Запишите закон движения для движения МТ с постоянным ускорением.
Для движения с постоянным ускорением закон движения
 , где
, где  - начальное положение и
- начальное положение и  - начальная скорость МТ.
- начальная скорость МТ.
12. Запишите закон изменения скорости для движения МТ с постоянным ускорением.
Закон скорости:  .
.
13. Дайте определение пути при произвольном движении МТ.
При произвольном движении МТ путь есть сумма длин отрезков траектории, при движении по которым направление движения не менялось.
14. Напишите формулу для вычисления пути при произвольном движении МТ.
Формула для вычисления пути за время  :
: 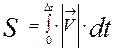
15. Дайте определение средней скорости. Напишите формулу для ее вычисления.
Средняя скорость – отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Для характеристики движения вводится понятие средней скорости:

16. Дайте определение тангенциального ускорения.
ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется величина скорости  ; оно направлено по касательной к траектории.
; оно направлено по касательной к траектории.
17. Дайте определение нормального ускорения.
НОРМАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется направление вектора скорости  (R – радиус кривизны траектории). Оно перпендикулярно касательной.
(R – радиус кривизны траектории). Оно перпендикулярно касательной.
18. Напишите формулу для вычисления величины полного ускорения по известным тангенциальному и нормальному ускорениям.
Полное ускорение определяется по теореме Пифагора: 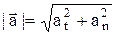
19. Как движется МТ, если ускорение остается все время направленным вдоль скорости?
Если ускорение все время направлено вдоль скорости, то МТ движется ускоренно по прямой линии.
20. Как движется МТ, если ускорение все время направлено против скорости?
Если ускорение остается все время направленным против скорости, то МТ движется замедленно по прямой линии.
21. Как движется МТ, если ускорение все время остается направленным перпендикулярно скорости?
Если ускорение остается все время направленным перпендикулярно скорости, то МТ движется равномерно по окружности.
22. Как движется МТ, если скорость все время направлена вдоль радиус-вектора?
Если скорость все время направлена вдоль радиус-вектора, то МТ движется прямолинейно по направлению от начала координат.
23. Как движется МТ, если скорость все время направлена против радиус-вектора?
Если скорость все время направлена против радиус-вектора, то МТ движется прямолинейно по направлению к началу координат.
24. Как движется МТ, если скорость все время направлена перпендикулярно радиус-вектору?
Если скорость все время направлена перпендикулярно радиус-вектору, то МТ движется по окружности с центром в начале координат.






