Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.
Измерение – нахождение значения физической величины опытным путем с помощью средств измерения.
Прямое измерение – определение значения физической величины непосредственно средствами измерения.
Косвенное измерение – определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемые прямыми измерениями.
Никакие измерения не делаются абсолютно точно. Они всегда производятся с некоторой погрешностью, связанной с несовершенством средств измерения и другими причинами. Но и при наличии погрешностей имеется несколько способов проведения достоверных измерений и вычисления отклонения от точного значения.
Абсолютной погрешностью называется отклонение от точного значения:
,
где Δа – абсолютная погрешность,
ат – точное значение измеряемой величины,
а – измеренное значение.
Абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности (определяется конструкцией прибора) и абсолютной погрешности отсчета (связана с неправильным снятием показаний прибора).
Абсолютную погрешность измерения округляют до такого же разряда, что и значения измерений.
При нескольких измерениях часто вычисляют среднее значение нескольких величин. Для этого сумму величин делят на их количество:
,
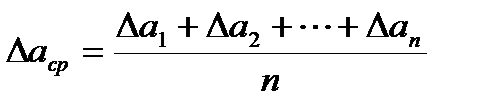где Δаср – среднее значение абсолютной погрешности,
n – количество приближенных измерений (величин).
Относительная погрешность измерения физической величины равна отношению среднего значения абсолютной погрешности к точному значению, выраженному в процентах:
100%,
где ε – относительна погрешность.
Ход работы
1. Решить задачу 1 двумя способами
2. Решить задачу 2
3. Ответить на вопросы
Вычисления
Задача 1.
Решить задачу 1, если заданы значения:
ат – точное значение числа,
а1,а2,а3 – приближенные значения числа.
Найти среднее значение абсолютной погрешности ∆аср, относительную погрешность ε.
Способ 1:
1. Абсолютная погрешность каждого значения приближенного числа:
,
∆a1=
∆a2=
∆a3=
2. Среднее значение абсолютной погрешности: 
,
∆аср=
3. Относительная погрешность: 100%
ε=
Способ 2:
1. Среднее значение приближенных величин: 
, аср=
2. Абсолютная погрешность: 
, ∆aср=
3. Относительная погрешность: ε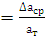 
100% ε=
Задача 2.
Решить задачу 2, когда не задано точное значение величины, а известны только ее приближенные значения:
а1,а2,а3 – приближенные значения числа;
Найти среднее значение абсолютной погрешности ∆аср, относительную погрешность ε.
1. Среднее значение приближенных величин, принимаемое за точное значение: 
,
аср=
2. Абсолютная погрешность каждого значения приближенного числа:
,
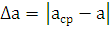∆a1=
∆a2=
∆a3=
3. Среднее значение абсолютной погрешности: ,
∆аср=
4. Относительная погрешность: 
100%
ε=
Вывод
Записать ответы на вопросы полными предложениями:
1) Что называется погрешностью?
2) Что такое абсолютная погрешность? Как ее вычислить?
3) Что такое относительная погрешность? Как ее вычислить?
4) Как вычислить среднее значение нескольких величин?
ЛАБОРАТОРНАЯ РАБОТА 2
