F1(x)=0,
F2(x)=0,
…
Fn(x)=0
с помощью MS Excel. Для этого в пакете существует так называемый блок решения, вызвать который можно командой Сервис®Поиск Решения. Диалоговое окно, которое появится после выполнения этой команды, изображено на рис. 6.8.
Назначение основных кнопок диалогового окна Поиск решения:
· Поле Установить целевую ячейку -определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению.
· Опции «минимальному значению», «максимальному значению» и «значению», определяют, что необходимо сделать со значением целевой ячейки - максимизировать, минимизировать или сделать равным конкретному значению.
· Поле Изменяя ячейки определяет изменяемые ячейки. Изменяемая ячейка — это ячейка, которая может быть изменена в процессе поиска решения для достижения нужного результата в ячейке из окна Установить целевую ячейку с удовлетворением поставленных ограничений.
· Кнопка Предположить отыскивает все не формульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки.
· Окно Ограничения перечисляет текущие ограничения в данной задаче. Ограничение это условие, которое должно удовлетворяться решением; ограничения перечисляются в виде ячеек или интервалов ячеек, обычно содержащих формулу, которая зависит от одной или нескольких изменяемых ячеек, чье значение должно попадать внутрь определенных границ или удовлетворять равенству.
· Кнопки Добавить, Изменить, Удалить позволяют добавить, изменить или удалить ограничение.
· Кнопка Выполнить запускает процесс решения определенной задачи.
· Кнопка Закрыть закрывает окно диалога, не решая проблемы. Сохраняются лишь изменения, сделанные при помощи кнопок Параметры, Добавить, Изменить и Удалить. Не сохраняются изменения, произведенные после использования данных кнопок.
· Кнопка Параметры выводит окно диалога Параметры поиска решения, в котором можно контролировать различные аспекты процесса отыскания решения, а также загрузить или сохранить некоторые параметры, такие, как выделение ячеек и ограничений, для какой-то конкретной задачи на рабочем листе.
· Кнопка Восстановить очищает все текущие установки задачи и возвращает все параметры к их значениям по умолчанию.
Итак, для решения системы уравнений задачу необходимо сформулировать одним из следующих способов.
1. Найти минимум (максимум) функции  , при системе ограничений, заданной в виде равенств Fi(x)=0.
, при системе ограничений, заданной в виде равенств Fi(x)=0.
2. Найти минимум функции  . В этом случае задача решается без ограничений.
. В этом случае задача решается без ограничений.
ПРИМЕР 5.3. Решить систему уравнений 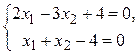 .
.
1 способ. В ячейки А1 и А2 введем число 0 (здесь мы будем хранить x 1 и x 2). В ячейки В1 и В2 введем ограничения: В1=2*А1-3*А2, В2 =А1+А2. В ячейку С1 введем функцию цели (эту ячейку мы будем минимизировать): С1=СУММ(B1:B2). Воспользуемся командой Сервис®Поиск Решения и заполним появившееся диалоговое окно так, как показано на рис. 6.8. В результате решения поставленной задачи получим решение системы исходных уравнений: x1=1.6, x2=2.4.
2 способ. В ячейках D1 и D2 будем хранить переменные x1 и x2. В ячейки E1 и E2 введем уравнения системы: E1=2*D1-3*D2+4, E2=D1+D2-4. В качестве функции цели в ячейку F1 введем формулу = E1^2+E2^2. Обратимся к решающему блоку (рис. 6.9) и заполним диалоговое окно. В результате получаем следующее решение системы: x1= 1,600000128, x2= 2,39999949.

Рис. 5.8

Рис. 5.9
ПРИМЕР 5.4. Решить систему уравнений  .
.
Прежде чем воспользоваться описанными выше методами решения систем уравнений, найдем графическое решение этой системы. Отметим, что оба уравнения системы заданы неявно и для построения графиков, функций соответствующих этим уравнениям, необходимо разрешить заданные уравнения относительно переменной y.
Для первого уравнения системы имеем:
 .
.
Выясним ОДЗ полученной функции:

Второе уравнение данной системы описывает окружность. Подробно о построении подобных линий см. в ПРИМЕРЕ 4.5.
На рис.6.10 приведен фрагмент рабочего листа MS Excel с формулами, которые необходимо ввести в ячейки для построения линий, описанных уравнениями системы. Точки пересечения линий изображенных на рис.6.11 являются графическим решением системы нелинейных уравнений.


Рис. 6.10 Рис. 5.11
Не трудно заметить, что заданная система имеет два решения. Поэтому процедуру поиска решений системы необходимо выполнить дважды, предварительно определив интервал изоляции корней (см. ПРИМЕРЫ 5.1 и 6.2) по осям Оx и Oy. В нашем случае первый корень лежит в интервалах (-0.5;0) x и (0.5;1) y, а второй - (0;0.5) x и (-0.5;-1) y. Далее поступим следующим образом. Введем начальные значения переменных x и y, формулы отображающие уравнения системы и функцию цели, так как показано на рис 5.12.

Рис. 5.12
Теперь дважды воспользуемся командой Сервис®Поиск Решения, заполняя появляющиеся диалоговые окна, так как показано на рис. 6.13 и 6.14.

Рис. 5.13

Рис. 6.14
На рис.6.15 приведены результаты вычислений. Сравнив полученное решение системы с графическим, убеждаемся, что система решена верно.

Рис. 5.15
ЛАБОРАТОРНАЯ РАБОТА №5
ВАРИАНТЫ ЗАДАНИЙ
ЗАДАНИЕ 5.1. Найти корни полинома.
| № | уравнение | № | уравнение |
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a) 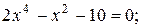 b)
b) 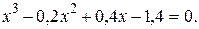
| a)  b)
b) 
| ||
a)  b)
b) 
| a) 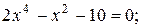 b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 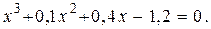
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a) 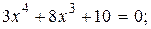 b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
| ||
a)  b)
b) 
| a)  b)
b) 
|
ЗАДАНИЕ 5.2. Найти решение нелинейного уравнения.
| № | уравнение | № | уравнение | № | уравнение |
a)  b)
b) 
| a)  b)
b) 
| a) 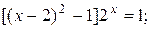 b)
b) 
| |||
a)  b)
b) 
| a) 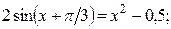 b)
b) 
| a)  b)
b) 
| |||
a) 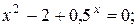 b)
b) 
| a) 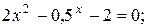 b)
b) 
| a)  b)
b) 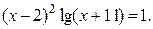
| |||
a)  b)
b) 
| a)  b)
b) 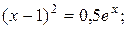
| a) 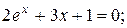 b)
b) 
| |||
a)  b)
b) 
| a) 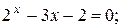 b)
b) 
| a)  b)
b) 
| |||
a)  b)
b) 
| a)  b)
b) 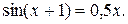
| a)  b)
b) 
| |||
a)  b)
b) 
| a) 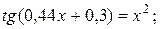 b)
b) 
| a)  ;
b) ;
b) 
| |||
a)  b)
b) 
| a)  b)
b) 
| a)  b)
b) 
| |||
a)  b)
b) 
| a)  b)
b) 
| a)  b)
b) 
|
ЗАДАНИЕ 5.3. Найти решение системы нелинейных уравнений.
| № | Система уравнений | № | Система уравнений | № | Система уравнений |


| 

| 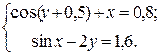

| |||


| 

| 

| |||


| 

| 

| |||
| № | Система уравнений | № | Система уравнений | № | Система уравнений |
 
|  
|  
| |||
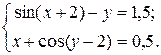 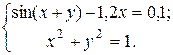
| 20- |  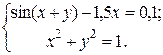
|  
| ||
 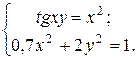
| 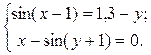 
|  
| |||
 
|  
|  
| |||
 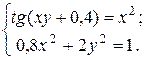
|  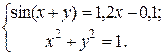
|  
| |||
 
|  
|  
| |||
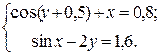 
| 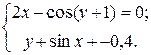 
|  
|






