Этот расчет производится для того, чтобы запроектировать продольную рабочую арматуру. Определить диаметр и количество стержней.
При расчете сечений, имеющих полку в сжатой зоне, следует ограничивать значение ее расчетной ширины beff из условия, что размер свеса полки в каждую сторону от ребра должен быть не более 1/6 пролета элемента и не более:
· при наличии поперечных ребер или при hf' ³ 0.1×h равным 1/2 расстояния в свету между продольными ребрами;
· при отсутствии поперечных ребер или при расстоянии между ними большем, чем расстояние между продольными ребрами, и hf' < 0.1×h равным 6hf';
· при консольных свесах полки:
1. при hf' ³ 0.1×h равным 6hf';
2. при 0.05×h £ hf' £ 0.1 равным 3hf';
3. при hf' < 0.05×h – свесы не учитываются.
При расчете железобетонных элементов, имеющих тавровое сечение с полкой в сжатой зоне, принято рассматривать два расчетных случая в зависимости от положения нейтральной оси (рис. 3.6). Если нейтральная ось располагается в пределах полки (рис. 3.6,а,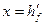 
) к расчету принимают прямоугольное сечение с размерами beff ´ h. Это вытекает из принятого допущения о том, что сопротивление бетона растянутой зоны в расчете не учитывается. Если нейтральная ось располагается в ребре (рис. 3.6,б), сжатая зона имеет сложную форму, включая и часть ребра. Границей между двумя рассматриваемыми случаями является расчетная ситуация, при которой нейтральная ось располагается по грани полки при 
.
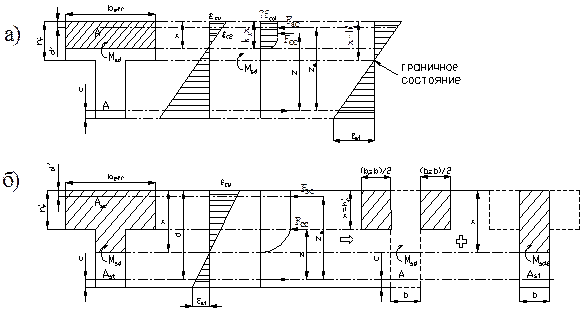
Рис. 3.6. К расчету тавровых (двутавровых) сечений изгибаемых элементов: а) нейтральная ось проходит в полке (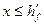
); б) нейтральная ось проходит в стенке (
);
Для таврового (двутаврового) сечения с одиночным армированием условие, определяющее положение нейтральной оси в сечении, можно записать:
 ,
| (3.3.1) |
Для таврового (двутаврового) сечения с двойным армированием
| (3.3.2) |
Если условие выполняется, это означает, что нейтральная ось располагается в пределах полки и сечение рассчитывают как прямоугольное.
Если условие не выполняется, производят расчет таврового сечения, для которого равнодействующая усилий в сжатом бетоне определяется в соответствие с рис. 3.6.б
 ,
| (3.3.3) |
Тогда момент относительно растянутой арматуры в общем случае можно записать:
|
| (3.3.4) |
Подставив,
 ,
| (3.3.5) |
получаем квадратное уравнение относительно 
 ,
| (3.3.6) |
где:
 ,
| (3.3.7) |
Решая квадратное уравнение (3.3.6) получаем:
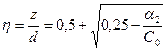
| (3.3.8) |
Подбор арматуры
Если выполняется условие 
и напряжения в растянутой арматуре достигают расчетного сопротивления (при этом нет необходимости усиливать сжатую зону), ее площадь находят из условия равновесия продольных сил:
 ,
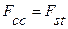| (3.3.9) |
где Fcc − равнодействующая усилий в сжатом бетоне, определяемая по формуле:
 ,
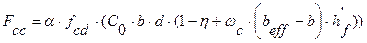| (3.3.10) |
Тогда площадь растянутой арматуры:
 ,
| (3.3.11) |
В случае если условие не выполняется, первоначально определяют площадь арматуры в сжатой зоне Asс по формуле:
 ,
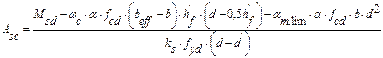| (3.3.12) |
Площадь растянутой арматуры в этом случае определится из условия:
.
Тогда:
 ,
| (3.3.13) |
где: 
.
Проверка прочности.
В случае, когда нейтральная ось сечения располагается в стенке таврового сечения, высоту сжатой зоны х (в предположении достижения предельных деформаций сжатым бетоном и растянутой арматурой) определяют из условия равновесия в сечении продольных усилий:
 ,
| (3.3.14) |
Если x £ xlim, т.е. выполняется условие , предельный момент относительно растянутой арматуры определяют по:
|
| (3.3.15) |
Если x > xlim, т.е. сечение переармировано, при расчете предельного момента принимают x = xlim, либо выполняют расчет по общему методу.
