Вопрос Мощность. КПД
Любая машина, которая используется для выполнения работы, характеризуется особой величиной, которая называется мощностью.
Мощность - это физическая величина, равная отношению работы ко времени, за который эта работа была выполнена. Мощность обозначается буквой N и в Системе Интернациональной измеряется в ваттах, в честь английского ученого 18-19 века Джеймса Уатта. Если мощность известна, то работу, которая выполняется за единицу времени, можно найти как произведение мощности на время. Поэтому за единицу работы можно взять работу, которая выполняется за 1 секунду при мощности 1 ватт. Такая единица работы называется ватт-секундой (Вт • с).
Коэффициент полезного действия (КПД) - это физическая величина, равная отношению полезной работы к полной работы. КПД обозначается буквой η и измеряется в процентах. Полезная работа всегда меньше полной. КПД всегда меньше 100%.
Вопрос7
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=MB(F). Таким образом, лемма о параллельном переносе силы доказана.
Вопрос8
Теорема Вариньона о моменте равнодействующей.
Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Рассмотрим систему сил, F1,F2 …,Fn, сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.
Для доказательства теоремы найдем соответствующие выражения моментов m0(F1), m0(F2), …. По формуле 
. Но, как видно из рисунка, 
, где F1x - проекция силы на ось Ох; следовательно 
Аналогично вычисляются моменты всех других сил.
Обозначим равнодействующую сил, 
, 
…, 
, через, где 
. Тогда, по теореме о проекции суммы сил на ось, получим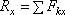 
. Умножая обе части этого равенства на ОА, найдем: 
или, 
.
