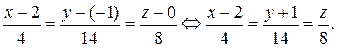Уравнение прямой, проходящей через заданную точку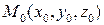 
параллельно вектору 
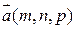имеет вид:
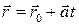(1)
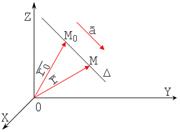
и называется векторно-параметрическим уравнением прямой. Здесь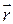 
– радиус-вектор произвольной точки М(x,y,z) прямой; 
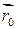– радиус-вектор фиксированной точки 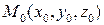, t – параметр, принимающий всевозможные действительные значения. Вектор 
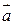называется направляющим вектором прямой, а его координаты 
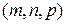– направляющими коэффициентами прямой.
Если в уравнении (1) перейти к координатам векторов, то получаются параметрические уравнения прямой:
(2)
Если из уравнений (2) исключить параметр t, то получаются канонические уравнения прямой:
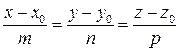(3)
Уравнения прямой, проходящей через две точки М1(x1,y1,z1) и М2(x2,y2,z2) имеют вид:
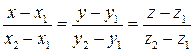(4)
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей
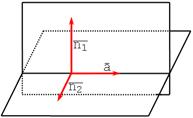
Т.о., прямая определяется совместным заданием системы двух линейных уравнений:
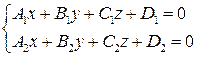(5)
---------------------------------------------------------------------------------------------------------------- Прямая в пространстве. Стр. 1.
Они называются общими уравнениями прямой. В этом случае направляющий вектор прямой можно определить следующим образом:
.
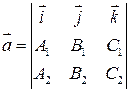Пусть заданы две прямые: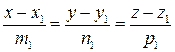 
и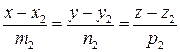 
. Тогда условие параллельности прямых записывается в виде: 
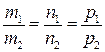, условие перпендикулярности – в виде: 
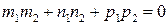, а угол 
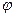между ними вычисляется по формуле
.
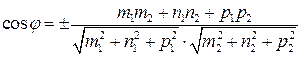Пример 1. Составить уравнения прямой, проходящей через точку M 1(2;0;–3) параллельно: а) вектору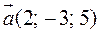 
; б) прямой 
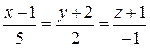; в) оси Ox.
Решение. а) Так как искомая прямая параллельна вектору 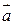, то этот вектор можно принять за ее направляющий вектор. Тогда канонические уравнения искомой прямой имеют вид:
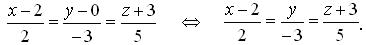
б) Так как искомая прямая параллельна прямой с направляющим вектором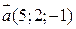 
, то этот вектор параллелен искомой прямой, значит, его можно принять за направляющий вектор искомой прямой. Тогда канонические уравнения искомой прямой имеют вид:
.
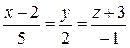в) Так как искомая прямая параллельна оси Ox, значит, она параллельна вектору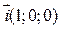 
, т.е. 
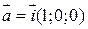и канонические уравнения искомой прямой имеют вид:
.
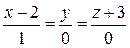Случай, когда хотя бы в одном знаменателе канонических уравнений прямой получается ноль, не лишено смысла, но свидетельствует о том, что направляющий вектор прямой имеет одну или две нулевые координаты. В таких случаях лучше записывать параметрические уравнения прямой:
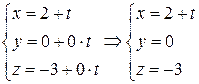
---------------------------------------------------------------------------------------------------------------- Прямая в пространстве. Стр. 2.
Пример 2. Составить канонические уравнения прямой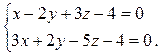 
Решение. Для составления канонических уравнений прямой необходимо знать направляющий вектор 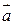и какую-нибудь фиксированную точку на прямой M 0. Направляющий вектор 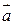вычислим как векторное произведение нормальных векторов плоскостей, эту прямую образующих. Т.к. 
, 
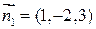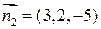, то
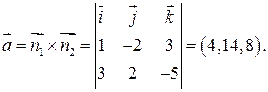
В качестве фиксированной точки можно выбрать любую точку прямой. Зададим одну из координат искомой точки произвольно. Пусть z=0. Тогда
.
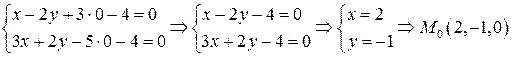Теперь составляем канонические уравнения прямой, зная ее направляющий вектор 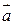и фиксированную точку M 0: 
