Уравнения динамики и энергетического баланса при качении тел по наклонным поверхностям

 

3.1. Уравнения динамики и расчёты коэффициента сопротивления качению

 

В данной работе рассматривается качение для плоского типа движения тела. Движение твёрдого тела называется плоским (или плоско – параллельным), если тело, перемещаясь в пространстве, совершает повороты, не имея закреплённых точек, и при этом каждая точка тела движется в одной и той же плоскости, параллельной некоторой неподвижной плоскости.

Плоское движение могут совершать тела разной формы, в данном случае: стальной шар, катящийся по наклонным поверхностям. Исследуемое тело (шар) является однородным, так что центр его масс совпадает с центром симметрии. Следует подчеркнуть, что только при выполнении этого условия траектория центра масс повторяет профиль опорной поверхности, вдоль которой перемещается вместе с катящимся телом ось мгновенного вращения. В классической механике доказано, что в этом случае для теоретических расчётов можно использовать уравнение динамики вращательного движения тела относительно мгновенной оси в виде:

(6)

Здесь: e - угловое ускорение;

J_p и M_p – момент инерции и суммарный момент внешних сил относительно мгновенной оси, проходящей через точку касания между телом и опорой поверхностью (обозначается буквой P, см. рис. 2).

w,e

z

y

x

C

Ms

Vc, ac

a

Для более детальных расчётов уравнение (6) дополняют: условием кинематической связи между ускорением центра масс а_с и угловым ускорением тела e; уравнением динамики движения центра масс (II закон динамики Ньютона) и уравнением динамики вращательного движения тела относительно

G

P

Fсц

Рис.2

 

оси, проходящей через центр масс параллельно мгновенной оси в т. Р.

На рис. 2 изображено однородное тело (шар радиусом r), скатывающееся без скольжения по наклонной поверхности. Направление поворота с угловыми

скоростью w и ускорением e показано изогнутой стрелкой (при этом векторы и направлены вдоль оси Y). Показаны направления скорости V_c и ускорения a_c центра масс тела – т. С. В т. Р – м. ц. с. и здесь приложена сила F_сц. Сила тяжести G всегда приложена в центре масс. Пара сил с моментом сопротивления M_s обозначена здесь изогнутой стрелкой (силы N и G_N, образующие эту пару сил, показаны на рис 1б).

Принимая, что скатывающееся тело совершает плоское движение, запишем полную систему уравнений динамики в проекциях на оси координат (см. рис. 2):

 

 

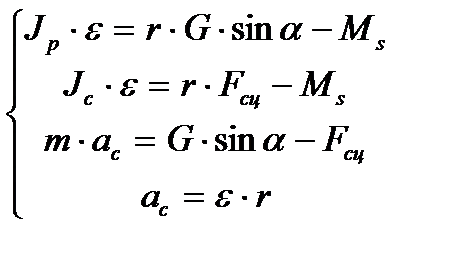
Система уравнений (7) дана с учётом момента сопротивления M_s, который действует при вычислении моментов сил как относительно т. Р, так и относительно т. С. Соотношение (7 г) – это условие кинематической связи между a_c и e, выполняющееся только при качении без скольжения.

Уравнения (7) описывают качение ведомого тела, и сила F_сц направлена противоположно ускорению центра масс a_c. Отметим, что с ростом угла наклона a величиной M_s для упрощения некоторых расчётов можно пренебречь, т. к. в (7а) sin a - возрастает, а в (7б), где F_сц и M_s зависят от величины cos a, надо учитывать, что всегда значения коэффициентов d<<m. Это условие было использовано при выводе формулы (2) для предельного значения коэффициента m, обеспечивающего сцепление с ростом угла наклона.

Общий вид решения для ускорения a_c, скорости V_c и длины пути l _c центра масс тела легко получается из уравнения (7а) при условиях постоянства угла наклона a и момента сопротивления M_s. При этих условиях движение тела является равнопеременным, т. е. качением с постоянными угловым ускорением e и ускорением центра масс a _c. Для скатывающегося шара с радиусом r такие решения имеют вид:

 

(8а)

(8б)

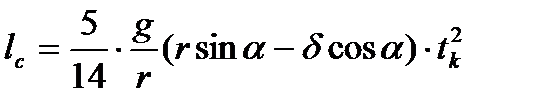(8в)

 

Здесь: t_k – время скатывания;

l _c – длина прямолинейного пути центра масс шара.

Из (8в) получаем следующую формулу для коэффициента сопротивления качению d:

 

(9)

 

Формулу (9) можно, в принципе, использовать для определения величины d, измеряя в эксперименте время скатывания t_k на пути l_c при заданном угле наклона. Однако, как показывает предварительный анализ, постановка таких измерений нецелесообразна, т. к. требует громоздких устройств и особо точных приборов.

Это объясняется тем, что значения коэффициентов d обычно невелики. Например, при качении стальных шариков по стальным поверхностям значения d лежат в интервале: d = (1 – 5)×10^-3 см. Несложный анализ формулы (8в) показывает, что при таких значениях d ожидаемая разница времён скатывания без учёта и с учётом сопротивления качению даже на длине l_c» 100 м при углах a» (5 – 10)° лежит в интервале (0,1 – 0,2) сек при времени скатывания t_k» (14 – -15) сек.

Такая малая разность времён скатывания "маскируется" погрешностями измерений параметров в формуле (9). Следовательно, результаты измерений коэффициента d на основе решений уравнений динамики (7) не дают достоверных сведений о его величине, если в опытах не используется особо точная (и, соответственно, дорогая) аппаратура.

В следующем разделе 3.2 рассмотрена более простая методика определения коэффициента d, основанная на применении уравнения энергетического баланса.

 

3.2. Уравнение энергетического баланса и методика определения коэффициента сопротивления качению

 

Уравнение энергетического баланса – это математическая формулировка общефизического закона сохранения энергии. Для установок, где механическая энергия может – под действием непотенциальных сил – преобразовываться в другие формы энергии, уравнение баланса имеет вид:

 

(10)

 

Здесь: Е₀ – начальная механическая энергия;

E(t) – механическая энергия в момент времени t;

E_s – потери механической энергии, обусловленные работой непотенциальных сил.

Уравнение (10) позволяет в ряде случаев выполнять исследования более простыми методами, чем с применением системы уравнений динамики, например, типа (7) для качения тел.

Рассмотрим методику определения коэффициента сопротивления качению d с учётом уравнения (10) на установке "Механический лоток". Принципиальная схема такой установки дана на рис. 3.

a

hi

li

a

hN

l0

lN

b

h0

Рис. 3.

 

Установка состоит из двух наклонных плоскостей с равными углами наклона. Исследуемое тело – шар может перекатываться с одной плоскости на другую по желобу, обеспечивающему плоско – параллельный тип движения при качении.

Поднятое в верхнее положение и покоящееся тело имеет начальную механическую энергию Е₀, равную потенциальной энергии П₀ = mgh₀, где h₀ – высота подъёма центра масс, отсчитываемая от нижнего уровня спуска (см.

рис. 3).

Механическая энергия при движении в произвольный момент времени t равна:

, (11)

где П(t) = mgh; 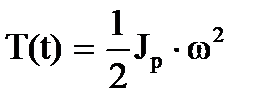- потенциальная и кинетическая энергии при качении без скольжения.

Если допустить, что потери механической энергии при качении отсутствуют (E_s = 0), тогда тело, перекатываясь с одной плоскости на другую, в моменты остановок (когда ω = 0) поднималось бы на одну и ту же высоту, равную h₀. Этот вывод легко проверить теоретически, подставляя формулу (11) в уравнение (10). При условии, что E_s = 0 и кинетическая энергия в момент времени t_k остановки T(t_k) = 0, получим: П₀ = П(t_k), т.е. высота h в момент остановки тела должна равняться начальной высоте h₀.

В опыте, однако, наблюдается уменьшение высоты подъёма тела после каждого очередного перекатывания. На схеме рис.3 показан шар, поднявшийся на высоту h_N после числа перекатываний, равного N. Поскольку в моменты остановок кинетическая энергия равна нулю, из (10) и (11) получаем:

 

(12)

 

Здесь: E_s – потери энергии, равные работе момента сопротивления качению A_s за всё время движения.

Используя формулу (5), получаем:

 

(13)

 

Здесь: φ – полный угол поворота шара при качении, который определяется простым выражением:

 

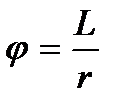, (14)

 

где L – длина пути центра масс шара за время катаний с одной плоскости на другую.

Схема, приведённая на рис.3, позволяет найти для расчёта величины L следующую простую формулу:

 

(15)

 

Из схемы на рис.3 также видно, что высоты h₀ и h_N можно найти с помощью выражений:

 

(16)

 

Подставляя (13), (14), (16) в уравнение (12) и учитывая: , получим выражение для расчёта коэффициента сопротивления качению в следующем виде:

 

, (17)

 

где: ‹ b › = ‹ l₀ › - ‹ l_N › – разность отсчётов расстояний от нижней точки спуска до центра шара;

‹ L ›– вычисляется с помощью формулы (15).

Выражение (17) показывает, что использование закона сохранения энергии (в форме уравнения энергетического баланса) позволяет проводить опыты для определения коэффициента δ без измерения времени движения. Требуются только линейные измерения величин b и L. Экспериментальная установка при этом может иметь небольшие размеры.

Кроме того, значительно повышается достоверность результатов измерения коэффициента δ по сравнению с результатами, получаемыми по формуле (9). Это объясняется тем, что погрешности линейных измерений параметров в формуле (17) обеспечивают для коэффициента δ доверительный интервал, величина которого на два порядка меньше среднего значения δ, получаемого в опыте.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

4.1. Экспериментальная часть

 

Лабораторная работа состоит из двух заданий. Для выполнения первого задания требуется один стальной шарик; для второго задания – два одинаковых стальных шарика.

Технические данные установки указаны на месте и в конце подраздела 4.1. Значения этих величин в расчётах принять константами.

Измерения выполняются на установке «Механический лоток», принципиальная схема которой показана на рис.3. Основной деталью установки является стальная полоса длиной 204 см, симметрично изогнутая в средней части радиусом R₁. На поверхности полосы по всей её длине проточен жёлоб с радиусом R₂, предназначенный для катания шариков с радиусом

r ≤ 1,5 см.

Глубина и ширина жёлоба, радиусы R₁ и R₂, размеры участков, сопряжённых радиусом R₁, указаны на схеме установки, имеющейся в лаборатории. Там же указано среднее значение угла наклона плоскостей < α > и погрешность Δ α, так что угол наклона определён в интервале: α = < α > ± Δα.

Изогнутая стальная полоса стационарно закреплена с помощью опор на горизонтальной станине. Вдоль полосы имеется миллиметровая шкала, предназначенная для измерения расстояний от нижней точки изгиба, которая является также нижней точкой спуска при скатывании шарика. Погрешность измерений на шкале (ошибка прибора) равна: Δ_пр = 0,2 см.

По заданию преподавателя могут быть использованы полосы из других материалов – дерева и пластмассы, которые укладываются инженером на время выполнения работы поверх стальной полосы.

Масса шарика m = (44,15 ±0,05) г, радиус шарика r = (1,105 ±0,002) см, угол наклона жёлоба α = (6,5 ±0,1)^о.

 

4.1.1. Экспериментальные задания и обработка результатов

 

Примечание. Количество заданий устанавливает преподаватель. Жёлоб для катания шариков должен быть чистым от пыли и иных загрязнений.

 

Задание № 1. Измерение коэффициента сопротивления качению для стальных шариков.

 

Опыт удобнее выполнять вдвоём, т.к. при этом сокращается время эксперимента. Один участник опыта располагается у правого конца установки, другой – у левого.

Необходимо заранее приготовить таблицу (по форме таблицы 1-1) для записи результатов прямых измерений.

Выполните несколько пробных пусков шарика для тренировки в правильных измерениях по шкале. Расстояния от средней части жёлоба до центра шарика отсчитываются как справа, так и слева в моменты остановок шарика с точностью до десятых долей сантиметра.

Измерения проводятся в следующем порядке:

1) Установите шарик в верхнем положении справа и запишите отсчёт l₀ в таблицу 1-1.

2) Отпустите (без толчка) шарик, который катится сначала вниз, затем – вверх и останавливается первый раз. Запишите отсчёт l₁ в таблицу 1-1.

3) Шарик катится после первой остановки вниз, затем – вверх и останавливается второй раз. Запишите отсчёт l₂ в таблицу 1-1.

4) Шарик продолжает кататься по жёлобу, уменьшая при этом высоту подъёма. Необходимо фиксировать и записывать отсчёты расстояний в течение 10 катаний шарика.

5) После записи отсчёта l_N с номером N = 10 остановите шарик. Повторите опыт согласно п.п. 1-4 десять раз, заполняя таблицу 1-1.

Примечание. Для выполнения всего цикла измерений в задании № 1 требуется время, не превышающее 10 минут.

Таблица 1-1

 

l, см	Количество измерений, n	<l>, см
l0
l1
l2
l3
l4
l5
l6
l7
l8
l9
l10

 

Данные таблицы 1-1 являются результатами прямых измерений. Обработка этих результатов состоит в расчёте средних значений расстояний и погрешности их измерений. Средние значения < l > занесите в таблицу 1-1.

При вычислении погрешности каждого из десяти значений l₁ – l₁₀ учтите случайную статистическую ошибку при доверительной вероятности 0,95 и систематическую ошибку шкалы, равную Δ_пр = ±0,2 см. Ошибку округления можно не учитывать ввиду её малой величины по сравнению с другими ошибками.

Коэффициент сопротивления качению δ определяется формулой (17), т. е. его величина является результатом косвенного измерения. В формулу (17) подставьте средние значения величин: <b>, <L> и tg<α>.

Средние значения <b> и <L> вычисляются по формулам раздела 3.2 при подстановке в них средних величин < l >, найденных с помощью таблицы 1-1. При вычислении < b>, <L> и tg<α > необходимо сохранять 4-5 значащих цифр (с учётом округления).

Результаты вычислений <b>, <L>, tg<α> и среднего значения коэффициента < δ >, а также погрешностей этих величин занесите в таблицу 1-2. При вычислении погрешностей сохраняйте одну-две значащие цифры.

 

Таблица 1-2

<b>, см	Δb, см	<L>, см	ΔL, см	tg<α>	Δ(tgα)	<δ>, см	Δδ, см

 

Погрешности вычисляются с помощью формул:

(18)

 

Необходимо провести доказательство вывода формул (18). Здесь значение Δ δ определяет величину доверительного интервала для найденного в опыте коэффициента сопротивления качению:

 

(19)

 

При расчёте погрешностей руководствуйтесь методическим пособием №100.

 

Замечание к заданию № 1

 

Необходимо отметить, что данная здесь методика определения коэффициента сопротивления качению приводит к систематической ошибке в результате измерения. Эта ошибка невелика: ~1%, т.е. не меняет ни порядка, ни главных двух значащих цифр у получаемой в опыте величины коэффициента δ. Несколько завышается третья значащая цифра результата измерения.

Появление систематической ошибки объясняется конструкцией установки, а именно, наличием участка окружности с радиусом R ₁, обеспечивающего плавный переход с одной наклонной плоскости на другую при катании шарика. На этом участке момент сопротивления качению M_s становится переменным по двум причинам:

1) изменяется проекция силы тяжести G_N, т. к. меняется угол наклона поверхности;

2) центр масс шарика получает добавочное ускорение при движении по дуге окружности с радиусом R₁, и, следовательно, появляется дополнительное давление на поверхности из-за действия центростремительной силы.

Названные причины ведут к некоторому увеличению суммарной работы момента сопротивления. Теоретический вывод уточнённых формул здесь не приводится. Однако студенты, интересующиеся физикой и механикой, могут самостоятельно получить формулы для расчёта работы момента сопротивления качению на участке дуги с радиусом R₁ (эти размеры указаны на схеме установки в лаборатории) и определить уточнённое значение коэффициента сопротивления качению. Такие расчёты, как отмечено выше, приведут к незначительному уменьшению величины коэффициента δ по сравнению с результатом, полученным по методике задания №1.

 

Задание №2. Исследование столкновения стальных шариков при качении

 

Пояснение к заданию №2

 

Для выполнения эксперимента требуются два стальных шарика с равными радиусами r и массами m. Эти параметры шариков указаны отдельно. В опыте один шарик устанавливается на середине механического лотка. Второй шарик вначале устанавливается в верхней точке и затем отпускается и катится вниз по жёлобу до столкновения с первым шариком.

Столкновение в данном случае является центральным, т. к. вектор скорости набегающего шарика расположен (при ударе) на линии, соединяющей центры шариков. При этом столкновение можно считать упругим, т. к. в опыте используются шарики, предназначенные для подшипников качения (потерями энергии при столкновении таких шариков в данном опыте можно пренебречь).

Напомним, что при поступательном движении свободно летящих шаров для расчётов упругих столкновений используются законы сохранения импульса и механической энергии. Как известно, эти расчёты показывают, что при центральном столкновении шаров с равными массами происходит обмен импульсом таким образом, что при ударе летящего шара по неподвижному – движущийся шар полностью теряет свою скорость (останавливается), а другой – получает скорость, равную скорости шара, движущегося до столкновения.

Однако столкновения катящихся шаров происходят иначе. Это объясняется тем, что тела при качении вращаются, и, следовательно, действуют законы сохранения и изменения момента импульса (разумеется, совместно с такими же законами для импульса и энергии).

В опыте, который проводится на установке "Механический лоток", при столкновении шариков наблюдается следующее явление. После удара скатившегося вниз шарика по неподвижному – оба шарика затем начинают катиться в одном направлении, но с разными скоростями. Первый (вначале неподвижный) шарик получает более высокую начальную скорость и катится вверх по жёлобу до остановки на расстоянии, превышающем половину расстояния от нижней до верхней точки жёлоба. Второй шарик после столкновения некоторое время (этот интервал хотя и небольшой, но заметен без специальных приборов) остается на месте, а затем вдруг начинает катиться вслед первому. Начальная скорость движения второго шарика меньше, и он катится вверх по жёлобу, проходя до остановки более короткое расстояние, чем первый шарик.

Примечание. Студентам, интересующимся физикой и механикой, предлагается самостоятельно описать физический механизм наблюдаемого явления. Решить соответствующую систему уравнений динамики и доказать, что при центральном упругом столкновении нормально катящегося шара со скоростью центра масс V_0c – с неподвижным шаром (радиусы и массы шаров равные) получается следующий результат:

а) первый (ранее неподвижный) шар начинает нормально катиться со скоростью центра масс V_1c = 5/7 V_0c, (учесть, что нормальное качение начинается не сразу после удара при столкновении);

б) второй шар (имевший перед столкновением скорость центра масс V_0c) начинает нормально катиться вслед за первым со скоростью центра масс V_2c = 2/7 V_0c (учесть, что нормальное качение начинается не сразу после удара при столкновении).

Расчёты выполнять для столкновения на горизонтальной поверхности, т. к. удар по неподвижному шару в проводимом опыте происходит на горизонтали – в нижней части механического лотка. Объяснить причину уменьшения суммарной кинетической энергии шаров после столкновения по сравнению с кинетической энергией до столкновения.

Первая цель эксперимента в задании №2 состоит в сравнении начальной кинетической энергии нормального качения шариков после столкновения с потенциальной энергией шариков в моменты остановок после качения вверх по жёлобу.

Считаем известным, что угловые скорости шариков в начале нормального качения после столкновения определяются выражениями:

 

(20)

 

Здесь: ω₀₁ – угловая скорость первого шарика (покоящегося до столкновения);

ω₀₂ – угловая скорость второго шарика, имевшего до столкновения скорость ω₀.

Формулы (20) верны только для центрального упругого столкновения шаров с равными радиусами и массами.

Угловая скорость ω₀ определяется в опыте с помощью уравнения энергетического баланса:

, (21)

 

где: h₀ – высота подъёма центра масс второго шарика в момент пуска;

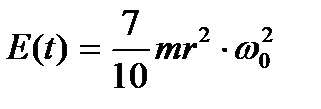– кинетическая энергия второго шарика в момент времени перед столкновением;

E_s – потери энергии при качении, которые можно рассчитать приближённо по формуле: (здесь: l_c – длина пути центра масс от точки пуска до точки столкновения; δ – коэффициент сопротивления качению, найденный в Задании №1; α – угол наклона плоскости качения).

Напомним, что потери энергии можно вычислять более точно, разделяя движение шарика на качение по поверхности с постоянным углом наклона α и по дуге окружности радиусом R₁. Однако в данном опыте достаточно приближённого расчёта величины E_s.

После определения угловой скорости ω₀ вычисляются (с учётом (20)) значения начальной механической энергии нормального качения шариков после столкновения:

 

(22)

 

Здесь учтено, что механическая энергия равна кинетической энергии шариков, т. к. столкновение происходит в нижней точке спуска.

Если принять условие, что дальнейшее качение шариков происходит без потерь механической энергии (т. е. сопротивлением качению можно пренебречь), тогда, используя закон сохранения механической энергии, получим:

 

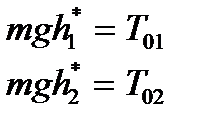(23)

 

где h₁^* и h₂^* – теоретические высоты подъёма центров масс шариков в момент остановки (после качения без потерь энергии).

Значения h₁^* и h₂^* легко вычислить, использую формулы (23) и данные о величине ω₀. Однако в опыте будут получаться значения высот h₁ < h₁^* и h₂ < h₂^*, т. к. имеются потери энергии, равные работе A_s момента сопротивления качению. Работы A_s1 и A_s2 моментов сопротивления при качении первого и второго шариков до остановки определяются с учётом результатов опыта по формулам:

 

(24)

 

Второй целью эксперимента в задании №2 является опытное подтверждение соотношения начальных скоростей качения шариков после столкновения. Согласно формулам (20) отношение начальных угловых скоростей равно:

(25)

 

Заметим, что это соотношение верно также и для скоростей центров масс шариков после столкновения.

Легко проверить, применяя формулы (22) и (23), что для отношения высот h₁^* и h₂^* получается:

 

(26)

 

В опыте измеряются реальные высоты подъёма центров масс шариков, совершающих качение при наличии сопротивления. Потери энергии при качении шариков до остановки на высотах h₁ и h₂ вносят некоторое отклонение от теоретического значения отношения скоростей ω₀₁ и ω₀₂, определяемого формулой (25). Такие отклонения составляют обычно несколько процентов и могут быть учтены строгим расчётом работы момента сопротивления качению. Однако в данной работе достаточно качественного подтверждения соотношения (26) с использованием значений высот h₁ и h₂, найденных в эксперименте.

 

4.1.2. Измерения и обработка результатов

 

4.4.1. Установите первый шарик в нижней части жёлоба так, чтобы его центр находился на расстоянии (5 – 10) мм слева от начала шкалы отсчёта. Эту точку установки не всегда удается фиксировать в опыте постоянной и по этой причине необходимо занести в таблицу 2-1 её положение в виде начальной координаты x₀₁ центра масс первого шарика.

4.4.2. Установите второй шарик в верхней части жёлоба справа. Отметьте положение центра масс шарика на шкале в виде расстояния l₀ (значение l₀ будет повторяться в следующих опытах, так что эту величину можно записать один раз).

4.4.3. Отпустите (без толчка) второй шарик и наблюдайте за его качением и последующим столкновением с первым шариком в нижней точке спуска.

4.4.4. После столкновения первый и второй шарики начинают катиться влево, поднимаясь по жёлобу вверх, и затем останавливаются. Зафиксируйте и занесите в таблицу 2-1 отсчёты по шкале в виде координат x₁ и x₂ центров масс первого и второго шариков в моменты их остановок в верхней точке подъёма.

4.4.5. Повторите опыты 10 раз, занося результаты отсчётов по шкале в таблицу 2-1.

Таблица 2-1

х, см	Номер опыта	<x>, см
x01
x1
x2

 

Таблица 2-1 содержит результаты прямых измерений. Обработка этих результатов состоит в определении средних значений < x₀₁>, <x₁> и <x₂>, которые следует занести в последнюю графу таблицы 2-1.

Все остальные данные получаются с помощью формул, т. е. являются результатом косвенных измерений. Погрешности измерений вычисляются по отдельному указанию преподавателя. Основные расчёты выполняются для средних значений по формулам, приведённым в разделе "Пояснение к заданию №2".

Вначале следует найти значения высот h₀, h₁ и h₂, используя для этого данные опыта (т. е. значения l₀, <x₁> и <x₂>) и схему установки, имеющуюся в лаборатории.

Вычислите длину пути центра масс l_c при скатывании второго шарика до столкновения с первым по формуле: l_c = l₀ – <x₀₂>, где < x₀₂> = 2r – <x₀₁> – средняя координата центра масс второго шарика в момент столкновения.

Используя уравнение энергетического баланса (21), найдите величину w₀. Затем вычислите значения начальных кинетических энергий Т₀₁ и Т₀₂ шариков после столкновения и значения высот h₁^* и h₂^* подъёма шариков по жёлобу при отсутствии потерь механической энергии.

По формулам (24) вычислите работу моментов сопротивления качению, определяющую потери энергии при качении шариков до остановки после столкновения.

Последний результат: соотношение скоростей шариков после столкновения – определяется с помощью формулы (26), куда подставляются значения высот h₁ и h₂, найденные в опыте.

 

ВОПРОСЫ ДЛЯ ПРОВЕРКИ (ПРИМЕРНЫЕ)

 

5.1. Объяснить цель опытов, схему установки и методику выполнения эксперимента.

5.2. Какое механическое движение называется нормальным качением? Условия нормального качения тел.

5.3. Понятие момента сопротивления качению. Работа момента сопротивления качению.

5.4. Уравнения динамики качения по наклонной поверхности.

5.5. Уравнение энергетического баланса при качении тел.

5.6. На каком расстоянии от начальной точки остановится шарик радиусом

r=1см при качении по горизонтальной поверхности с коэффициентом сопротивления качению d = 2×10^-3 см при начальной скорости центра масс V _0c =

=1 м/с и 10 м/с?

5.7. Понятие работы силы. По какой причине работа сил сцепления при нормальном качении тел равна нулю?

5.8. Объяснить, как вычисляется высота подъёма центра масс шарика, если точка его остановки находится на дуге окружности с радиусом R ₁, величина которого указана на схеме установки.

5.9. По какой причине столкновения шаров при качении отличаются от столкновений свободно летящих шаров?

5.10. Объяснить результаты опытов Задания №1.

5.11. Объяснить результаты опытов Задания №2.

ЛИТЕРАТУРА

 

6.1. Д. В. Сивухин. Общий курс физики, т. 1, "Механика". М., Наука, 1974, 519с.

6.2. Н. В. Крагельский, В. С. Щедров. Развитие науки о трении. М., Издание АН СССР, 1956, 235с.

6.3. Н. В. Крагельский, И. Э. Виноградова. Коэффициенты трения. М., Машгиз, 1962.

6.4. К. Джонсон. Механика контактного взаимодействия. М., Мир, 1989.

6.5. Г. В. Дедков. Нанотрибология: экспериментальные факты и теоретические модели. Успехи физических наук, т. 170, №6, 2000, с.585-618.

6.6. А,Д.Терентьев. Введение в физику: основы физических измерений, Методическое пособие № 100, КГТУ, 2006г.

ПРИЛОЖЕНИЕ