Поиск
Поиск является одной из основных операций при обработке информации в ЭВМ. Ее назначение - по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу.
Набор данных (любых) будем называть таблицей или файлом. Любое данное (или элемент структуры) отличается каким-то признаком от других данных. Этот признак называется ключом. Ключ может быть уникальным, т. е. в таблице существует только одно данное с этим ключом. Такой уникальный ключ называется первичным. Вторичный ключ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных могут быть собраны в одном месте (в другой таблице) или представлять собой запись, в которой одно из полей - это ключ. Ключи, которые выделены из таблицы данных и организованы в свой файл, называются внешними ключами. Если ключ находится в записи, то он называется внутренним.
Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие его в таблице. В случае отсутствия данного возможны две операции:
1. индикация того, что данного нет
2. вставка данного в таблицу.
Пусть k - массив ключей. Для каждого k(i) существует r(i) - данное. Key - аргумент поиска. Ему соответствует информационная запись rec. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.
Последовательный поиск
Применяется в том случае, если неизвестна организация данных или данные неупорядочены. Тогда производится последовательный просмотр по всей таблице начиная от младшего адреса в оперативной памяти и кончая самым старшим.
Последовательный поиск в массиве (переменная search хранит номер найденного элемента).

for i:=1 to n
if k(i) = key then
search = i
return
endif
next i
search = 0
return
На Паскале программа будет выглядеть следующим образом:
for i:=1 to n do
if k[i] = key then
begin
search = i;
exit;
end;
search = 0;
exit;
Эффективность последовательного поиска в массиве можно определить как количество производимых сравнений М. Мmin = 1, Mmax = n. Если данные расположены равновероятно во всех ячейках массива, то Мср» (n + 1)/2.
Если элемент не найден в таблице и необходимо произвести вставку, то последние 2 оператора заменяются на
n = n + 1 на Паскале
k(n) = key n:=n+1;
r(n) = rec k[n]:=key;
search = n r[n]:=rec;
return search:=n;
exit;
Если таблица данных задана в виде односвязного списка, то производится последовательный поиск в списке (рис. 5.2).

Варианты алгоритмов:
| На псевдокоде: q=nil p=table while (p <> nil) do if k(p) = key then search = p return endif q = p p = nxt(p) endwhile s = getnode k(s) = key r(s) = rec nxt(s) = nil if q = nil then table = s else nxt(q) = s endif search = s return | На Паскале: q:=nil; p:=table; while (p <> nil) do begin if p^.k = key then begin search = p; exit; end; q:= p; p:= p^.nxt; end; New(s); s^.k:=key; s^.r:=rec; s.^nxt:= nil; if q = nil then table = s else q.^nxt = s; search:= s; exit |
Достоинством списковой структуры является ускоренный алгоритм удаления или вставки элемента в список, причем время вставки или удаления не зависит от количества элементов, а в массиве каждая вставка или удаление требуют передвижения примерно половины элементов. Эффективность поиска в списке примерно такая же, как и в массиве.
Эффективность последовательного поиска можно увеличить.
Пусть имеется возможность накапливать запросы за день, а ночью их обрабатывать. Когда запросы собраны, происходит их сортировка.
Индексно-последовательный поиск
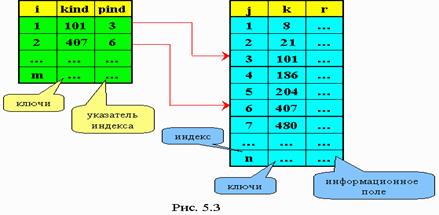
При таком поиске организуется две таблицы: таблица данных со своими ключами (упорядоченная по возрастанию) и таблица индексов, которая тоже состоит из ключей данных, но эти ключи взяты из основной таблицы через определенный интервал (рис. 5.3).
Сначала производится последовательный поиск в таблице индексов по заданному аргументу поиска. Как только мы проходим ключ, который оказался меньше заданного, то этим мы устанавливаем нижнюю границу поиска в основной таблице - low, а затем - верхнюю - hi, на которой (kind > key).
Например, key = 101.
Поиск идет не по всей таблице, а от low до hi.
Примеры программ:
| Псевдокод: i = 1 while (i <= m) and (kind(i) <= key) do i=i+1 endwhile if i = 1 then low = 1 else low = pind(i-1) endif if i = m+1 then hi = n else hi = pind(i)-1 endif for j=low to hi if key = k(j) then search=j return endif next j search=0 return | Паскаль: i:=1; while (i <= m) and (kind[i] <= key) do i=i+1; if i = 1 then low:=1 else low:=pind[i-1]; if i = m+1 then hi:=n else hi:=pind[i]-1; for j:=low to hi do if key = k[j] then begin search:=j; exit; end; search:=0; exit; |






