Знать: два определения линии в пространстве; уравнения прямой в пространстве; формулы углов между прямыми, между прямой и плоскостью; условия параллельности и перпендикулярности двух прямых, прямой и плоскости; условия принадлежности двух прямых одной плоскости и прямой плоскости; взаимное расположение двух прямых в пространстве, а также прямой и плоскости; формулы расстояния от точки до прямой в пространстве и между двумя скрещивающимися прямыми.
Уметь: переходить от одного вида уравнения прямой к другому; находить углы между прямыми, между прямой и плоскостью; находить расстояния в пространстве; устанавливать взаимное расположение прямых в пространстве, а также прямой и плоскости.
Проверочная работа «Уравнение плоскости в пространстве»
| 1 в. | 1. Составить уравнение плоскости, проходящей через основания перпендикуляров, опущенных из точки М(2;2;2) на координатные плоскости. | 2. При каких значениях  и и  уравнения уравнения 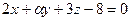 и и  будут определять параллельные плоскости? будут определять параллельные плоскости?
|
| 2 в. | 1. Составить уравнение плоскости, проходящей через точку М(1;0;3) и перпендикулярной к плоскостям 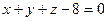 и и 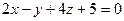 . .
| 2. При каких значениях  уравнения уравнения 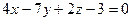 и и 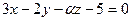 будут определять перпендикулярные плоскости? будут определять перпендикулярные плоскости?
|
Решение проверочной работы:
| 1 вариант | |
1. Из точки М на координатные плоскости можно опустить 3 перпендикуляра с основаниями М1(0;2;2), М2(2;0;2), М3(2;2;0).
Воспользуемся уравнением плоскости, проходящей через 3 данные точки, и получим:

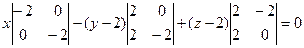
 Ответ: x+y+z-4=0.
Ответ: x+y+z-4=0.
| 2. 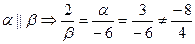
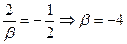
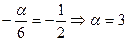 Ответ:
Ответ: 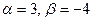 . .
|
| 2 вариант | |
1. 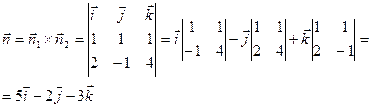 Воспользуемся уравнением плоскости, проходящей через точку М(1;0;3) и перпендикулярно вектору
Воспользуемся уравнением плоскости, проходящей через точку М(1;0;3) и перпендикулярно вектору  , получим , получим 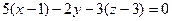
 Ответ:
Ответ:  . .
| 2. 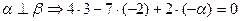  Ответ:
Ответ:  . .
|
Работа в аудитории:
1.3. Общее уравнение прямой  преобразовать к каноническому виду. преобразовать к каноническому виду.
| 1.4. Привести к каноническому виду прямую 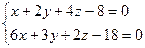 . .
| 1.5. Составить каноническое уравнение прямой, проходящей через точку М(4;3;-2) параллельно прямой 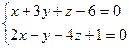 . .
|
| 2. Найти величину острого угла между прямыми | ||
2.3. 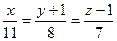 и и 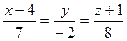 . .
| 2.4. 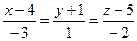 и и 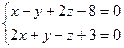 . .
| 2.5. 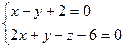 и и 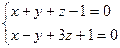 . .
|
| 3. Установить взаимное расположение прямых | ||
3.3.  и и  . .
| 3.4. 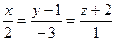 и и  . .
| 3.5.  и и  . .
|
4.3. Найти расстояние от точки М(-5;4;3) до прямой 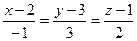 . .
| 4.4. Найти расстояние между параллельными прямыми  и и 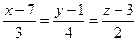 . .
| 4.5. Найти расстояние между скрещивающимися прямыми  и и 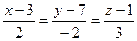 . .
|
5.3. Найти величину острого угла между прямой 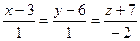 и плоскостью и плоскостью 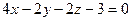 . .
| 5.4. Установить взаимное расположение прямой 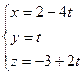 и плоскости и плоскости 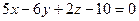 . .
| 5.5. Найти координаты точки, симметричной точке М(3;4;5) относительно плоскости 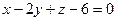 . .
|
Решения:
1.3. Общее уравнение прямой  преобразовать к каноническому виду.
преобразовать к каноническому виду.
 .
.
Пусть 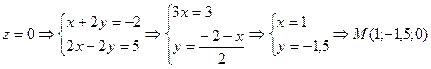 .
.
Воспользуемся каноническим уравнением прямой в пространстве 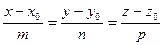 , где
, где 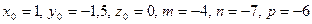 и получим
и получим 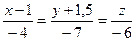
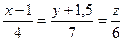
Ответ: 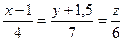 .
.
1.4. Привести к каноническому виду прямую 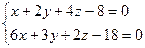 .
.
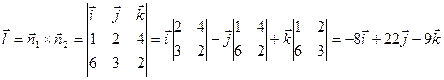 .
.
Пусть  .
.
Воспользуемся каноническим уравнением прямой в пространстве 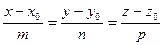 , где
, где 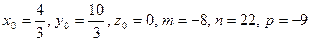 и получим
и получим 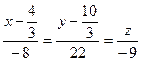
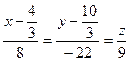 .
.
Ответ: 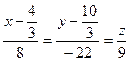 .
.
1.5. Составить каноническое уравнение прямой, проходящей через точку М(4;3;-2) параллельно прямой 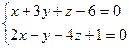 .
.
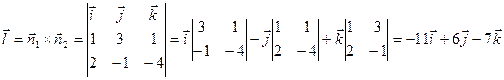 .
.
Воспользуемся каноническим уравнением прямой в пространстве 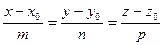 , где
, где 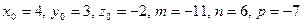 и получим
и получим 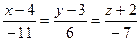
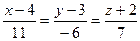
Ответ: 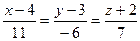 .
.
2.3. Найти величину острого угла между прямыми 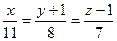 и
и 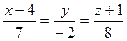 .
.
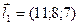
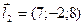
По формуле нахождения угла между двумя прямыми имеем
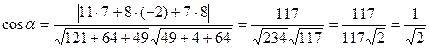
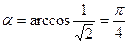
Ответ:  .
.
2.4. Найти величину острого угла между прямыми 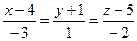 и
и 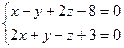 .
.

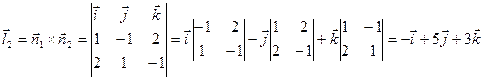
По формуле нахождения угла между двумя прямыми имеем

Ответ: 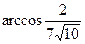 .
.
2.5. Найти величину острого угла между прямыми 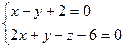 и
и 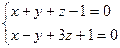 .
.

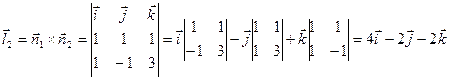
По формуле нахождения угла между двумя прямыми имеем
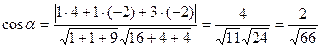
Ответ: 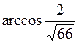 .
.
3.3. Установить взаимное расположение прямых  и
и  .
.
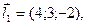
 .
.
Т.к.  , то прямые или параллельны, или совпадают.
, то прямые или параллельны, или совпадают.
Возьмем точку М1(2;0;-1) и подставим в уравнение 2-ой прямой.
 , т.е. точка не принадлежит 2-ой прямой.
, т.е. точка не принадлежит 2-ой прямой.
Ответ: параллельны.
3.4. Установить взаимное расположение прямых 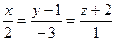 и
и  .
.
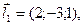
 .
.
Т.к.  , то прямые или пересекаются, или скрещиваются.
, то прямые или пересекаются, или скрещиваются.
Проверим условие принадлежности двух прямых 1-ой плоскости:
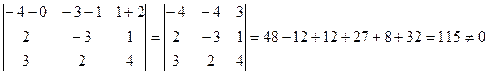 , т.е. прямые скрещиваются.
, т.е. прямые скрещиваются.
Т.к. 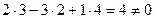 , то прямые не перпендикулярны.
, то прямые не перпендикулярны.
Ответ: скрещивающиеся.
3.5. Установить взаимное расположение прямых  и
и  .
.
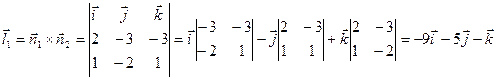
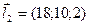 .
.
Т.к. 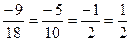 , то прямые или параллельны, или совпадают.
, то прямые или параллельны, или совпадают.
Возьмем точку М1(0;0;-3) и подставим в уравнение 1-ой прямой.
 , т.е. точка принадлежит 1-ой прямой.
, т.е. точка принадлежит 1-ой прямой.
Ответ: совпадают.
4.3. Найти расстояние от точки М(-5;4;3) до прямой 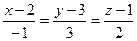 .
.
Воспользуемся формулой нахождения расстояния от точки до прямой 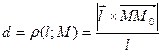 , где
, где  и М0(2;3;1),
и М0(2;3;1), 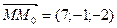
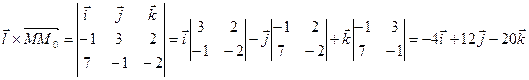
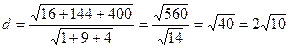
Ответ:  .
.
4.4. Найти расстояние между параллельными прямыми  и
и 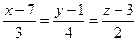 .
.
Т.к. расстояние между параллельными прямыми определяется как расстояние от любой точки 1-ой прямой до 2-ой прямой, то воспользуемся формулой нахождения расстояния от точки М(2;-1;0) до прямой 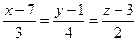 , где
, где 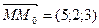 ,
, 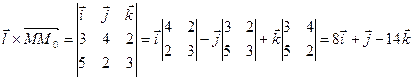 и получим
и получим  .
.
Ответ: 3.
4.5. Найти расстояние между скрещивающимися прямыми  и
и 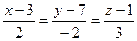 .
.
Воспользуемся формулой расстояния между скрещивающимися прямыми  , где
, где 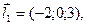
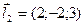 ,
,  ,
, 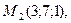
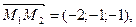
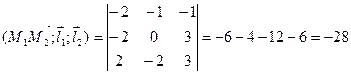 ,
,  ,
, 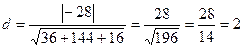 .
.
Ответ: 2.
5.3. Найти величину острого угла между прямой 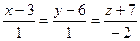 и плоскостью
и плоскостью 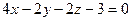 .
.
Воспользуемся формулой нахождения угла между прямой и плоскостью 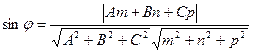 ,
, 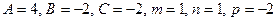 и получим
и получим  .
.
Ответ:  .
.
5.4. Установить взаимное расположение прямой 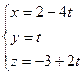 и плоскости
и плоскости 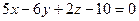 .
.
 и
и 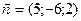 .
.
Т.к. 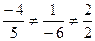 , то прямая и плоскость не перпендикулярны.
, то прямая и плоскость не перпендикулярны.
Т.к. 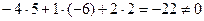 , то прямая и плоскость не параллельны.
, то прямая и плоскость не параллельны.
Ответ: пересекаются.
5.5. Найти координаты точки, симметричной точке М(3;4;5) относительно плоскости 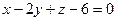 .
.
Пусть искомая точка А, тогда прямая АМ перпендикулярна данной плоскости. Воспользуемся уравнением прямой с направляющим вектором, который перпендикулярен плоскости 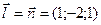 и проходящей через точку М(3;4;5):
и проходящей через точку М(3;4;5):  или
или 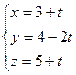 .
.
Найдем точку пересечения прямой АМ и данной плоскости, назовем ее точка В
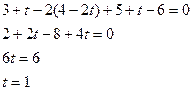
Т.е. точка В имеет координаты В(4;2;6).
Чтобы найти координаты точки А(x;y;z), воспользуемся тем, что В – середина АМ, т.е. 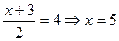 ,
, 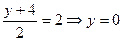 ,
,  .
.
Ответ: (5;0;7).






