Однофазный трансформатор
Цель работы: изучить устройство и принцип действия однофазного трансформатора, испытать его в режимах холостого хода, короткого замыкания и нагрузки, рассчитать параметры схемы замещения.
Принцип действия однофазного трансформатора
На рис. 1 схематично изображен однофазный понижающий трансформатор, имеющий обмотку ВН с числом витков W1 и обмотку НН с числом витков W2. вторичная обмотка разомкнута (режим хх), а к первичной обмотке подведено напряжение сети U1.
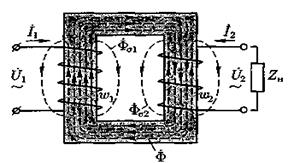 |
Рис.1
При подведении к обмотке ВН напряжения сети в ней потечет ток I1, который создаст магнитодвижущую силу (МДС)
F1 = I1*W1
МДС F1 формирует магнитный поток Ф1, основная часть которого замыкается по магнитопроводу (Ф0), и значительно меньшая часть замыкается по воздуху (Ф1S)
(в реальных силовых трансформаторах Ф0 = 0,95-0,96 Ф1)
Согласно закону электромагнитной индукции (е = 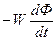 ) основной магнитный поток Ф0, сцепляясь с витками обмотки ВН, наводит в ней ЭДС самоиндукции, действующее значение которой равно Е1, и, пересекаясь с витками обмотки НН, наводит в ней ЭДС с действующим значением Е2. Магнитный поток Ф1S, сцепляясь с витками обмотки ВН, наводит в ней ЭДС рассеяния, действующее значение которой равно Е1S.
) основной магнитный поток Ф0, сцепляясь с витками обмотки ВН, наводит в ней ЭДС самоиндукции, действующее значение которой равно Е1, и, пересекаясь с витками обмотки НН, наводит в ней ЭДС с действующим значением Е2. Магнитный поток Ф1S, сцепляясь с витками обмотки ВН, наводит в ней ЭДС рассеяния, действующее значение которой равно Е1S.
Таким образом, при разомкнутой обмотке НН под действием напряжения U1 (в обмотке с числом витков W2) наводится ЭДС Е2, которая используется для питания нагрузки Zн вторичной цепи трансформаторов.
Из теории электрических цепей имеем:
| Е 1S = - jI1 X1 | (1) |
| E1 = 4,44 W1 f1 Ф | (2) |
| E2 = 4,44 W2 f1 Ф | (3) |
| Z 1 = R1 + j X1 | (4) |
| Z 2 = R2 + j X2 | (5) |
где f1– частота напряжения сети;
Z 1 , Z 2 – комплексы полных сопротивлений обмоток ВН и НН трансформатора;
R1, R2, – активные, X1, X2 – индуктивные сопротивления рассеяния обмоток ВН и НН трансформатора.
Количественная оценка уровней напряжения обмоток ВН и НН трансформатора осуществляется коэффициентом трансформации
K = 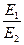 = = 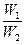 ≈ ≈ 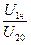
| (6) |
где U1н, U20 – напряжения обмоток ВН и НН в режиме хх (U20 = Е2).
Согласно второму закону Кирхгофа в установившемся режиме можно записать следующее уравнение электрического равновесия обмотки ВН
U1 + Е1 + Е1S = I1 R
На практике пользуются уравнением
| U1 = - Е1 + I1 R + jI1 X1 | (7) |
Режим нагрузки трансформатора
При замыкании обмотки НН на нагрузку в цепи этой обмотки возникает ток I2, который создаст МДС
F2 = I2 W2
МДС F2 размагничивает магнитопровод при индуктивной нагрузке и подмагничивает его при емкостной.
Режим нагрузки трансформатора характеризуется соотношением токов I1, I0 и I2. Если учесть, что при работе трансформатора в пределах номинальной нагрузки его магнитопровод ненасыщен и сделать следующее допущение
U1 ≈ Е1 = const,
то, используя формулу (2), можно записать условие:
Ф0 = 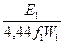 ≈ ≈ 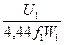 = const, = const,
| (8) |
суть которого заключается в том, что при изменении тока нагрузки I2 от нуля до номинального значения основной магнитный поток Ф0 остается неизменным (не зависит от нагрузки).
Условие (8) может быть выполнено в том случае, если справедливо равенство:
F0 = F1 + F2 = const,
или
| I0W1 = I1 W1 + I2 W2 = const | (9) |
Разделив обе части уравнения (9) на величину W1, получим уравнение токов трансформатора, работающего в режиме нагрузки:
I0 = I1 + I2 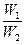
| (10) |
Обозначив I2 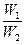 = I2
= I2 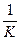 = I2′ – ток вторичной обмотки, приведенный к числу витков первичной обмотки, и решив последнее уравнение относительно тока I1, запишем уравнение токов в окончательном виде
= I2′ – ток вторичной обмотки, приведенный к числу витков первичной обмотки, и решив последнее уравнение относительно тока I1, запишем уравнение токов в окончательном виде
| I1 = I0 + (- I2′) | (11) |
Из уравнения (11) следует, что при работе трансформатора под нагрузкой условие (8) выполняется за счет изменения тока I1 в пределах, строго соответствующих диапазону изменения тока нагрузки I2′.
Приведенный трансформатор
Цель приведения – составить схему замещения трансформатора, обеспечивающую исследования и расчеты его основных режимов работы.
Условия приведения: физические процессы приведенного трансформатора должны быть аналогичны процессам реального трансформатора, то есть должны быть одинаковы мощности и углы сдвига фаз между векторами ЭДС, напряжений, токов приведенного и реального трансформаторов.
Схема замещения приведенного трансформатора показана на рис. 2б. Она содержит два контура: намагничивающий и рабочий (в котором протекает ток - I2′).
Поскольку на оба контура подается одно и то же напряжение, необходимо выполнить еще одно условие приведения трансформатора:
К = 1,
то есть W2′ = W1, где W2′ – число витков обмотки НН, приведенного трансформатора.
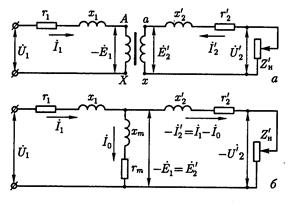 |
Рис.2
Обозначив индексом «штрих» величины приведенного трансформатора, можно записать:
| I2′ = I2/К | Z2′ = Z2 К2 |
| Е2′ = Е2/К | R2′ = R2 К2 |
| U2′ = U2/К | X2′ = X2 К2 |
Целесообразно также привести и нагрузку Zн к числу витков первичной обмотки трансформатора:
| Zн′ = Zн К2 | Rн′ = Rн К2 | Xн′ = Xн К2 |
На схеме намагничивающий контур показан последовательно соединенным активным Rm и индуктивным Xm сопротивлениями. Величина Rm эквивалентна сопротивлению контура, формирующему активные потери мощности в магнитопроводе трансформатора при возникновении тока I0. Величина Xm является сопротивлением взаимной индукции обмоток трансформатора.
По схеме замещения нетрудно составить уравнения электрического равновесия обмоток ВН и НН трансформатора на основе первого и второго законов Кирхгофа:
| U1 = - Е1 + I1 R + jI1 X1 Е2 = U′2 + I′2 R′2 + jI′2 X′2 I1 = I0 + (- I2′) |
В реальных условиях возможны следующие режимы работы трансформатора:
режим холостого хода (хх) – обмотка НН разомкнута;
режим нагрузки – обмотка НН замкнута на нагрузку Zн;
режим короткого замыкания (КЗ) – обмотка НН замкнута накоротко (Zн = 0),
ток I2 = max, то есть в десятки и сотни раз больше, чем I2ном

4. Испытание трансформатора косвенным методом
Для определения параметров и характеристик трансформатора проводят опыты ХХ и КЗ
Опыт холостого хода
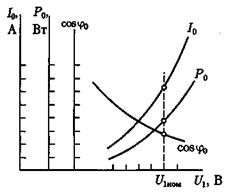 |
При разомкнутой вторичной обмотке на обмотку ВН подают напряжение U1 и, изменяя его в заданных пределах, измеряют U10, U20,I10,P0.
 |
Затем строят зависимости Zm, Rm, Xm, I10, P0, cosφ0 = f(U10)
Рис.3 Характеристики холостого хода трансформатора
Характер зависимостей можно объяснить следующим образом: активное сопротивление Rm = 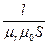 , т.е. Rm ~
, т.е. Rm ~ 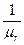 где μr – магнитная проницаемость материала магнитопровода. В свою очередь, значение величины μr изменяется в зависимости от напряженности магнитного поля (Н0 ~ I0) и степени насыщения магнитопровода.
где μr – магнитная проницаемость материала магнитопровода. В свою очередь, значение величины μr изменяется в зависимости от напряженности магнитного поля (Н0 ~ I0) и степени насыщения магнитопровода.
Мощность, измеряемая ваттметром, обусловлена потерями активной мощности в стали (Р0) и в обмотке ВН (ΔРэ1) трансформатора:
Рw = Р0 + ΔРэ1
Но поскольку Р0 ~ U210, ΔРэ1 ~ I20, а I0 = (0,02…0,1) I1ном, то в опыте ХХ потерями ΔРэ1 можно пренебречь. Следовательно,
| Рw ≈ Р0 | (13) |
По данным опыта ХХ вычисляют:
| К = U10 / U20 | (14) |
| cosφ0 = Р0/ U10 I0 | (15) |
| Zm = U10 / I0 | (16) |
| Rm = Р0 / I20 | (17) |
Xm = 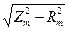
| (18) |
Примечание:
при правильно выполненных вычислениях Rm < Xm < Zm и cosφ0 = 0,15-0,3
Опыт короткого замыкания
При отключенном напряжении сети вторичную обмотку замыкают накоротко, затем подают напряжение на обмотку ВН и увеличивают его от нуля до значения, обеспечивающего возрастание тока I1 в пределах I1 = 1,1 I1ном
Задаваясь несколькими значениями тока I1, строят зависимости
I1к, Рк, cosφк,, Zк = f (U1к)
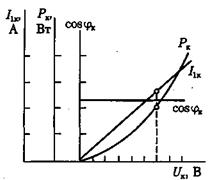 |
 Указанные зависимости имеют вид:
Указанные зависимости имеют вид:
Рис.4
Номинальное значение напряжения КЗ составляет 5-15% от значения U1ном. Поэтому трансформатор в опыте КЗ работает при ненасыщенном магнитопроводе, а, следовательно, Iк ~ Uк , cosφк = const; Zк = const
Мощность, измеренная ваттметром, содержит электрические потери
ΔРэк = ΔРэ1 + ΔРэ2
и потери в стали магнитопровода трансформатора Р0.
Причем
ΔРэ1 = I 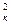 R1 R1
| ΔРэ2 = I 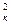 R R 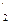
|
То есть ΔРэк = I 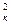 Rк,
Rк,
где Rк = R1 + R 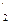 ≈ 2 R1 ≈ 2 R1
| (19) |
а Р0 ~ U 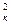
Но поскольку в опыте КЗ Iк = I1ном, а Uк мало, то потерями в стали магнитопровода пренебрегают, и следовательно
| Рw ≈ ΔРэк = Рк | (20) |
По измеренным значениям величин Iк, Uк и Рw вычисляют:
| Zк = Uк / Iк | (21) |
| Rк = Рк / I2к = R1 + R'2 ≈ 2 R1 | (22) |
Xк = 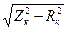 = X1 + X'2 ≈ 2 X1 = X1 + X'2 ≈ 2 X1
| (23) |
| uк% = Uк 100 / U1ном | (24) |
| uка% = Rк Iк100 / U1ном | (25) |
uкр% =  = Xк Iк 100 / U1ном = Xк Iк 100 / U1ном
| (26) |
| сosφк = Рк / Uк Iк | (27) |
В паспортных данных приводят номинальное значение напряжения короткого замыкания трансформатора uкн%, которое создает при замкнутой накоротко обмотке НН номинальные значения токов I1н и I2н.
Экспериментально-расчетные данные, полученные в опытах ХХ и КЗ, используют для вычисления значений:
оптимального коэффициента нагрузки трансформатора
βопт = 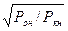
| (28) |
падения напряжения во вторичной обмотке
| Δu2 % = β (uка% сosφ2 + uкр% sin φ2) | (29) |
КПД трансформатора
| ή = Р2 /Р1 = Р2 / (Р2 + Р0 + β2 Рк ) | (30) |
Внешние характеристики.
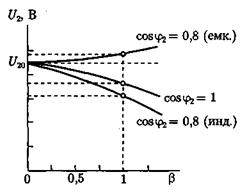 |
С увеличением нагрузки трансформатора напряжение на клеммах его вторичной обмотки изменяется. Зависимость этого напряжения от нагрузки выражается графически внешними характеристиками трансформатора U2 = f (I2). Вид внешней характеристики зависит от характера нагрузки и коэффициента мощности сosφ2: при активной и активно-индуктивной нагрузках внешние характеристики имеют падающий вид, причем чем меньше коэффициент мощности сosφ2 , тем больше наклон характеристики к оси абсцисс; при активно-емкостной нагрузке внешняя характеристика имеет восходящий вид (рис. 5).
Рис. 5
При любой нагрузке напряжение на клеммах вторичной обмотки трансформатора равно
| U2 = U20 (1 – 0,01 Δu2 %), | (31) |
где U20 = U2ном — напряжение на вторичной обмотке в режиме холостого хода, принимаемое за номинальное напряжение на выходе трансформатора, В;
Δu2 % – изменение вторичного напряжения, вызванное влиянием нагрузки трансформатора, %.
Для построения внешней характеристики трансформатора необходимо рассчитать не менее пяти значений вторичного напряжения U2 при разных значениях коэффициента нагрузки β = I2 / I2ном, например при β = 0,25; 0,50; 0,75; 1,0 и 1,2.
Расчет Δu2 % ведут по формуле (29)
Расчеты Δu2 % выполняют три раза: при сosφ2 = 1,0, сosφ2 = 0,8 (нагрузка активно-индуктивная) и сosφ2 = 0,8 (нагрузка активно-емкостная). В последнем случае получают отрицательные значения Δu2 %. По результатам вычислений строят на общей координатной сетке три внешние характеристики. Проведя ординату при β = 1,0 (номинальная нагрузка), отмечают на характеристиках напряжения, соответствующие номинальной нагрузке трансформатора.






