Методика измерения частотных (АЧХ и ФЧХ) характеристик в EWB

По определению, частотная характеристика параметра цепи есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде входного гармонического сигнала

H(jω) = Y_m/X_m.

Таким образом, частотная характеристика есть функция комплексной переменной jω – комплексной частоты, и ее называют комплексной частотной характеристикой (КЧХ), которую в показательной форме можно записать:

H(jω) = Y_m/X_m=(Y_mе^{j φy})/ (X_mе^{j φx}) = (Y_m/X_m)е^{j φ(ω)}

Из записанного выражения следует, что комплексная функция состоит из двух действительных функций:

1. H(ω) = Y_m/X_m – АЧХ;

2. φ(ω) = φ_y - φ_x - ФЧХ.

Измерение АЧХ и ФЧХ с помощью генератора и осциллографа слишком трудоемко, значительно проще проводить измерения с помощью измерителя диаграмм Боде, входящего в состав виртуальной электронной лаборатории EWB. Передняя панель и его выводы показаны на рис.1.1.

В режиме измерения АЧХ (Magnitude) на экран выводится график зависимости от частоты отношения U_my/U_mx, где U_my -амплитуда гармонического сигнала по напряжению на выводах OUT - “ВЫХОД”, а U_mx – амплитуда гармонического сигнала по напряжению на выводах IN - “ВХОД”. В режиме измерения ФЧХ (Phase) на экран выводится график зависимости от частоты фазового сдвига между гармоническими сигналами по напряжению U_my на выводах “ВЫХОД”, и - U_mx на выводах “ВХОД”.

Настройка измерителя заключается в выборе масштабов по осям: логарифмический (кнопка LOG) или линейный (кнопка LIN), и в выборе пределов измерения по вертикальной и горизонтальной осям с помощью кнопок в окошках F – максимальное значение и I – минимальное значение.

Измерение конкретных значений АЧХ и ФЧХ можно проводить с помощью вертикальной визирной линии, которая в исходном положении находится в начале координат и перемещается по экрану с помощью мыши или кнопками ←, →.

Значения измеряемой функции и ее аргумента в месте установки визирной линии индицируется в окошках в правом нижнем углу.

 

Так, к частотным передаточным характеристикам четырехполюсника относят комплексную функцию частотного коэффициента передачи напряжения К(jω)= U_2m/U_1m. Она представляет собой зависимость от частоты отношения комплексной амплитуды выходного напряжения к комплексной амплитуде напряжения на входе. Отсюда следует, что АЧХ передаточной функции напряжений есть К(ω)=U_2m/U_1m, а ФЧХ передаточной функции напряжений есть φ_к(ω)= φ₂- φ₁.

Следовательно, для измерения указанных характеристик клеммы ВХОД измерителя диаграмм Боде необходимо подсоединить ко входу исследуемого четырехполюсника, а клеммы ВЫХОД к выходу четырехполюсника.

Схема измерения частотных передаточных по напряжению характеристик цепи приведена на рис.1.2.

К входным частотным характеристикам четырехполюсника относят полное комплексное входное сопротивление Zвх(jω)=U_1m/I_1m. Оно представляет собой зависимость от частоты отношения комплексной амплитуды входного напряжения к комплексной амплитуде тока на входе. Отсюда следует, что АЧХ комплексной функции входного сопротивления есть Z(ω) =U_1m/I_1m, а ФЧХ передаточной функции напряжений есть φ_к(ω) = φ_u1- φ_I1.

Схема измерения частотных характеристик входного сопротивления четырехполюсника приведена на рис.1.3.

Для измерения входных характеристик клеммы ВЫХОД измерителя диаграмм Боде необходимо подсоединить ко входу исследуемого четырехполюсника, а клеммы ВХОД к дополнительному резистору R_доп, на котором создается напряжение, пропорциональное входному току.

Отсюда следует, что измеряемая характеристика представляет собой комплексную функцию входного сопротивления:

H(jω) = Ym/Xm= U_1m/I_1m=Zвх(jω)

Графики результатов измерения АЧХ и ФЧХ входного сопротивления, полученные в результате копирования в режиме Analysis Graphs, удобно использовать при оформлении отчета по курсовой работе. Чтобы скопировать изображение схемы или любого фрагмента, расположенного на рабочем столе программы EWB в отчет, подготавливаемый в текстовом редакторе Word, необходимо в меню Edit выделить команду Copy as Bitmap. После чего курсор мыши превращается в крестик, которым по правилу прямоугольника можно выделить нужную часть экрана. После отпускания левой кнопки мыши выделенная часть копируется в буфер обмена, содержимое которого может быть импортировано в любое приложение Windows.

Методика измерения импульсной и переходной характеристик следует из их определений. Схема измерения переходной характеристики приведена на рис.1.5.

Генератор необходимо поставить в режим формирования однополярных прямоугольных импульсов положительной полярности с амплитудой 1В (амплитуда –500мВ, смещение – 500мВ). Осциллограф – в режим синхронизации по каналу А. Затем получить на экране осциллографа устойчивое изображение выходного сигнала исследуемой цепи. Сигнал по каналу В и есть переходная характеристика цепи. Частоту генератора необходимо подобрать так, чтобы в пределах импульса выходной сигнал практически достигал своего стационарного значения.

Построение годографа

При графическом представлении комплексных частотных характеристик (КЧХ) Н(jω) цепи обычно отдельно строят графики АЧХ Н(ω) и ФЧХ φ_н(ω). Однако комплексную частотную характеристику можно представить на одном графике. Такой график называется годограф КЧХ и строится он в комплексной плоскости. Годограф КЧХ представляет собой геометрическое место точек концов вектора комплексной функции Н(jω) на комплексной плоскости при изменении частоты ω от 0 до ∞ (рис.1.6). Годограф иногда называют амплитудно-фазовой характеристикой цепи. График годографа позволяет одновременно судить как об АЧХ, а также об ФЧХ комплексной частотной характеристики.

Для построения годографа строится декартовая система координат, при этом по оси X откладывают реальную составляющую Re[Н(jω)] КЧХ, а по оси Y откладывают мнимую составляющую Jm[Н(jω)] КЧХ. На годографе указывают точки, соответствующие некоторым значениям частоты ω, и стрелкой показывают направление перемещения конца вектора Н(jω) при увеличении частоты. График годографа можно строить двумя способами.

По первому способу для построения графика можно использовать результаты расчета АЧХ Н(ω) и ФЧХ φ_н(ω), а точки графика годографа для заданного значения частоты ω_i наносить на комплексную плоскость аналогично тому, как это делается при построении графика в полярной системе координат.

По второму способу необходимо комплексную частотную характеристику Н(jω) записать в алгебраической форме Н(jω) = Re[Н(jω)] + jJm[Н(jω)], затем для определенных частот ω_i рассчитать значения Re[Н(jω)] = Н₁(ω_i) и Jm[Н(jω)] = Н₂(ω_i), и затем, как обычно, нанести эти точки на плоскость и соединив их, получить график.

 

 

ЗАДАНИЕ. Для предложенного варианта линейной цепи и заданных параметров:

1. Определить вид дифференциального уравнения, описывающего данную цепь, относительно именно тех входных и выходных параметров, которые указаны на схеме.

2. Найти частотный коэффициент передачи, его модуль и аргумент.

3. Построить графики АЧХ и ФЧХ данной системы.

4. Определить частотный коэффициент передачи мощности и передаточную функцию системы.

5. Найти комплексную функцию входного сопротивления Z_ВХ(jw), его АЧХ - Z_ВХ(w) и ФЧХ - j_z(w); построить графики.

6. Найти импульсную и переходную характеристики; построить их графики.

7. Определить характерные (резонансные) частоты.

8. Найти отклик цепи на прямоугольный импульс с амплитудой Е и длительностью t_и временным, классическим, спектральным и операторным методами; сравнить полученные разными методами результаты.

9. Составить схемы измерений частотных и переходных характеристик: Z_ВХ(w) и j_z(w); K_U(ω) и φ_k (ω); h(t); g(t) с использованием приборов электронной виртуальной лаборатории Electronics Workbench (EWB).

10. Построить графики характеристик, полученные в результате моделирования.

11. Провести анализ соответствия результатов аналитического расчета и эксперимента.

ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТОВ

Варианты:

 

23.

24.

25.

26.

27.

28.

 

29.

30.

31.

32.

33.

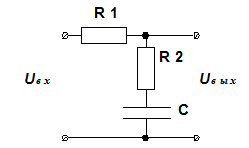
34.

 

Таблица соответствий вариантов и параметров:

Вариант	Параметры
R, Ом	L, мГн	С, мкФ	Е, В	τи , с
1.		0,5
2.
3.		0,4

Примечание:

1. Если в схеме два одинаковых элемента, то считать R₁ = 2R₂; L₁ = 2L₂;C₁ = 2C₂.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. При каких условиях реакцию линейной системы на короткий входной импульс можно считать импульсной характеристикой системы?

2. Как связаны между собой импульсная характеристика системы и ее частотный коэффициент передачи?

3. Какими способами можно определить частотный коэффициент передачи линейной стационарной системы? Выберите из них оптимальный, на Ваш взгляд, способ.

4. В чем состоит отличие динамических систем от стационарных?

5. В каких случаях и почему для анализа системы удобнее использовать частотный коэффициент передачи мощности?

6. При каких условиях RC-цепь можно считать дифференцирующей, а при каких – интегрирующей?

7. Исследуйте аналогичные условия (дифференцирования и интегрирования) для RL-цепи.

8. Проанализируйте и оцените достоинства и недостатки временного, спектрального и операторного методов анализа линейных стационарных систем.

9. Как определяется функция комплексного входного сопротивления цепи и в чем ее физический смысл?

10. Как определяются АЧХ и ФЧХ комплексного входного сопротивления?

11. В каких логарифмических единицах выражается усиление сигнала в системе?

12. Поясните принципы построения годографа и его практическую значимость.

 

ЛИТЕРАТУРА

1. Попов В. П. Основы теории цепей. – М.: Высшая школа, 2000.

2. Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1999.

1. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 1988.
2. Основы теории электрических цепей и электроники: Учебник для ВУЗов/ В.П.Бакалов, А.Н.Игнатов, Б.И.Крук. – М: Радио и связь, 1989.
3. Каяцкас А. А. Основы радиоэлектроники. - М., Высшая школа, 1988.
4. Бирюков В. Н. Попов В. П. Семенцова В. И. Сборник задач по теории цепей. – М.: Высшая школа, 1998.
5. Шебес М. Р. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.
6. Электротехника и электроника в экспериментах и упражнениях. Практикум на Electronics Workbench. В 2-х томах. Под ред. Д. И. Панфилова. - М.: Додэко, 2000.

 

Министерство образования Республики Беларусь

 

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им.Я.КУПАЛЫ»

 

 

Физико-технический факультет

 

 

Кафедра промышленной электроники

 

 

КУРСОВОЙ ПРОЕКТ

по курсу «Теория электрических цепей»

 

на тему: «АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМАХ»

Вариант № ___

 

Выполнил:

студент 2 курса 4 группы _____(подпись)______ __(дата)__ И.О.Фамилия

 

 

Проверил:

доцент кафедры промышленной

электроники, к.т.н. ___________________________________ Т.А.Ситкевич

 

Гродно, 2012