Задача 1. Написать программу печати таблицы значений функции  для аргумента, изменяющегося в заданных пределах с заданным шагом.
для аргумента, изменяющегося в заданных пределах с заданным шагом.
Задача 2. Дано натуральное число n.
а) Сколько цифр в числе n?
б) Чему равна сумма его цифр?
в) Найти первую цифру числа n.
Решить задачу, используя функции деления без остатка (div) и остатка от деления (mod) при делении на 10.
Задача 3. Вычислить с заданной точностью константу p, используя бесконечный ряд Шарпа (1699 г.):

Задача 4. Последовательность Хейеса:
Рассмотрим некоторое натуральное число n (n > 1). Если оно четно, то разделим его на 2, иначе умножим на 3 и прибавим 1. Если полученное число не равно 1, то повторяется то же действие (шаг) и т.д., пока не получится 1. Для первого натурального числа последовательность будет такой: 1 -> 4 -> 2 -> 1. Для числа 7: 7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1. Каждый раз приходим к замкнутому циклу 1->4->2->1!
Назовём вершиной наибольшее число в полученной при этом последовательности. Для заданного числа построить указанную последовательность, подсчитать число шагов и определить вершину.
Задача 5. Написать программу вычисления значения функции ex с помощью степенного ряда с точностью e по формуле:

Задания для контрольной работы
Вычислить и вывести на экран в виде таблицы значения функции, заданной с помощью ряда Тейлора, на интервале от xнач до xкон с шагом dx с точностью e. Таблицу снабдить заголовком и шапкой. Каждая строка таблицы должна содержать значение аргумента, значение функции и количество просуммированных членов ряда.
Вариант 1.

Вариант 2.

Вариант 3.
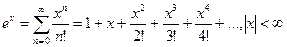
Вариант 4.

Вариант 5.

Вариант 6.

Вариант 7.

Вариант 8.

Вариант 9.

Вариант 10.

Вариант 11.

Вариант 12.

Вариант 13.

Вариант 14.

Вариант 15.

Вариант 16.

Вариант 17.

Вариант 18.

Вариант 19.

Вариант 20.

Одномерные массивы
Примеры решения заданий
Задача 1. Дано натуральное число n, действительные числа а1,а2,...,аn. Получить: a) max(a1,a2,...,an); б) min(a1, a2,..., аn).
Решение: Алгоритм решения задачи представлен на рис. 4.1.

Рис. 4.1. Блок-схема алгоритма решения задачи 1
Программа в Turbo Pascal будет иметь следующий вид:
Program max_min_mas;
Var a: Array [1..20] of Real;
n,i: 1..20;
min,max:Real;
Begin
Write('Введите число элементов массива (от_ 1 до 20)');
ReadLn(n);
WriteLn('Введите элементы массива ');
Write('l - й ');
ReadLn(a[l]);
max:=a[l]; min:=a[l];
For i:=2 to n do
Begin
Write(i,' - й ');
ReadLn (a[i]);
If a[i]>max then max:=a[i];
If a[i]<min then min:=a[i];
End;
WriteLn('Наибольший элемент массива: ',max);
WriteLn('Наименьший элемент массива: ',min);
End.
Задача 2. Даны натуральное число n, целые числа а1,...,аn. Подсчитать наибольшее число одинаковых, следующих подряд чисел.
Решение. Последовательность равных элементов массива назовём серией, а число k элементов в ней - длиной серии. Обозначим искомое число q. За один просмотр массива будем фиксировать начало каждой новой серии и в этот момент (a[i]<>a[i-l]) корректировать значение q с учётом длины закончившейся серии. Чтобы начать отсчет длины новой серии, здесь же сбросим накопленное значение переменной k (k:=1). Для учёта длины последней серии необходимо ещё одно сравнение величин q и к после выхода из цикла.
Алгоритм решения задачи представлен на рис. 4.2.

Рис. 4.2. Блок-схема алгоритма решения задачи 2
Программа в Turbo Pascal будет иметь следующий вид:
Program Count_max;
Const n=10;
a: Array [l..n] of Integer = _
(25,2,2,2,12,17,2,2,2,2);
Var i,k,q: 1..n;
Begin
k:=l; q:=l;
for i:=2 to n do
{начало или продолжение серии}
if a[i]=a[i-l]
then
Inc(k)
{конец серии из равных чисел}
else
begin
{замена текущего значения q }
if q<k then q:=k;
{новая инициализация счетчика}
k:=l
end;
{учёт последней серии}
if q<k then q:=k;
WriteLn(q);
ReadLn;
End.
Задача 3. Даны целые числа х, n, а1,..., аn (n>0). Определить, каким по счёту идет в последовательности а1,..., аn элемент, равный х. Если такого элемента нет, то предусмотреть соответствующее сообщение.
Решение. В этом примере мы сталкиваемся с задачей поиска. Различают поиск в упорядоченном и неупорядоченном массивах. В неупорядоченном массиве, если нет никакой дополнительной информации об элементе поиска, его выполняют с помощью последовательного просмотра всего массива и называют линейным поиском. Рассмотрим три варианта программы, реализующей этот метод. Очевидно, что в любом случае существуют два условия окончания поиска 1) элемент найден; 2) весь массив просмотрен и элемент не найден. Программа в Turbo Pascal, реализующая первый способ, имеет следующий вид:
Program Find_1;
Const
x=13; {элемент для поиска}
n=10;
a: Array [l..n] of Integer=_
(10,6,55,-1,13,6,29,-80,1,-16);
Var i:1..n;
Begin
i:=l;
While (a[i]<>x) and (i<n) do Inc(i);
If a[i]<>x
Then Write('Заданного элемента нет')
Else Write('Номер элемента: ', i);
End.
В цикле один оператор. Единственный способ ускорить поиск – упростить сложное логическое выражение. Поэтому в другом варианте применим приём фиктивного элемента, или барьера. Барьер - это дополнительный, (n+1)-ый элемент со значением х, расположенный в конце массива:
Program Find_2;
Const x=13; {элемент для поиска и барьер}
n=10;
a: Array [1..П+1] of Integer=_
(10,6,55,-1,13,6,29,-80,1,-16,х);
Var i: 1..n+1;
Begin
i:=l;
While a[i]<>x do Inc(i);
If i=n+l
Then Write('Заданного элемента нет')
Else Write('Номер элемента: ',i);
End.
Цикл обязательно завершится, так как гарантировано совпадение с барьером, а истинность равенства i = n + 1 будет свидетельствовать о том, что раньше совпадения не было, т.е. элемент не найден. Использование барьера с целью упрощения логических выражений – распространённый прием. Его применяют в программах, требующих скорости обработки данных.
Наконец, третий вариант программы использует процедуру Break, досрочно прерывающую работу циклов. Она позволяет применить оператор цикла For (пропущенный блок программы такой же, как в первом варианте).
Begin
For i:=l to n do
If a[i]=x then Break;
If a[i] <> x
Then Write('Заданного элемента нет')
Else Write('Номер элемента: ',i);
End.
Здесь необходимо отметить, что во всех вариантах программы, если элемент найден, то он первый из таких элементов в заданной последовательности.
Задача 4. Даны натуральные числа n, m и два целочисленных массива а1,..., аn и b1...,bm, упорядоченных по неубыванию. Образовать из элементов этих массивов упорядоченный по неубыванию массив c.
Решение. Рассмотрим вариант программы, использующий три последовательных цикла. В первом цикле, пока не будут исчерпаны элементы одного из массивов, после предварительного сравнения значений их текущих элементов, осуществляется запись в массив с. В каждый момент перед пересылкой a[i] либо b[j] в массиве с уже имеются (i-1) элементов массива а и (j-1) элементов массива b, то есть всего (i+j-2) значений. Поэтому индекс элемента с, которому присваивается очередное значение определяется по формуле: i+j-1. Заметим, что наращивание соответствующего индекса происходит в одной из ветвей условного оператора. Это обозначает, что значение второго индекса при этом не меняется, так что на следующем проходе цикла один из элементов будет участвовать в сравнении повторно.
Второй и третий последовательные циклы досылают оставшиеся элементы в конец результирующего массива Для второго цикла i+j-1 = i+m+1-1 = i+m, а для третьего i+j-1 = i+n+1-1 = i+n. Ясно, что на практике всегда работают только два из трёх циклов: первый и второй, если a[n]>b[m] или первый и третий, если a[n]<b[m].
Программа в Turbo Pascal будет иметь следующий вид:
Program Conc_mas;
Const n=12;
m=8;
Var a: Array [l..n] of Integer;
b: Array [l..m] of Integer;
c: Array [l..n+m] of Integer;
i,j,k: Integer;
Begin
{инициализация массивов а и b}
For i:=l to n do a[i]:=i*2;
For j:=l to m do b[j]:=j+9;
{заполнение массива с}
i:=l; j:=l;
While (i<=n) and (j<=m) do
If a[i]<=b[j]
then
begin
с[i+j-1]:=a[i];
Inc(i);
End
Else
begin
c[i+j-1]:=b[j];
Inc(j);
End;
While i<=n do
begin
с[m+i]:=a[i];
Inc(i);
End;
While j<=m do
begin
с[n+j]:=b[j];
Inc(j);
End;
{вывод образованного массива с}
For k:=l to m+n do Write(с[k]:8);
ReadLn;
End.
Задача 5. Выполнить внутреннюю сортировку массива n целых чисел а1, а2,..., аn по неубыванию.
Решение. Рассмотрим словесные описания алгоритмов и программы трёх простых методов внутренней сортировки массивов, их называют прямыми:
1. Сортировка с помощью включения.
2. Сортировка с помощью выбора.
3. Сортировка с помощью обменов.
Сортировка массива - это перерасположение элементов массива в заданном порядке (в текущей задаче: а1<а2<...<аn). Под внутренней сортировкой понимают сортировку, выполненную в оперативной памяти ЭВМ со случайным доступом без использования вспомогательного массива. Основная цель сортировки - облегчить последующий поиск.
1. Сортировка с помощью прямого включения.
Элементы массива, начиная со второго, последовательно берутся по одному и включаются на нужное место в уже упорядоченную часть массива, расположенную слева от текущего элемента ai. В отличие от стандартной ситуации включения элемента в заданную позицию массива, позиция включаемого элемента при этом неизвестна. Определим её, сравнивая в цикле поочерёдно аi с аi-1, аi-2,... до тех пор, пока не будет найден первый из элементов меньший или равный аi, либо не будет достигнут левый конец массива. Поскольку операции сравнения и перемещения чередуются друг с другом, то этот способ часто называют просеиванием или погружением.
Пусть массив а содержит 1000 сортируемых случайных чисел из отрезка [100, 999]. Переменная х - промежуточная величина, хранящая значение текущего элемента. Выше отмечалось, что при поиске позиции включения имеются два условия завершения цикла, поэтому используем барьер а0, присвоив ему значение х и расположив в начале массива, т.к. просмотр осуществляется слева направо. Диапазон индекса в описании массива расширим до 0..n. Переменная j при просмотре служит счётчиком цикла-просеивания, а после выхода из цикла – индексом включаемого элемента. Алгоритм решения задачи будет иметь вид, показанный на рис. 4.3.
 Программа в Turbo Pascal будет иметь следующий вид:
Программа в Turbo Pascal будет иметь следующий вид:
Program Sort_mas_1;
Uses Crt;
Const
n=1000;
Var
a: Array [0..n] of _ Integer;
x,j,i: Integer;
Begin
Randomize; {[100, 999]}
For i:=l to n do
begin
a[i]:=100+Random(900);
Write(a[i]:3);
End;
WriteLn;
Рис. 4.3. Блок-схема алгоритма решения задачи 5 (1)
For i:=2 to n do
begin
{x - промежуточная величина}
x:=a[i];
{a [0] - барьер}
a[0]:=a[i];
{j-счетчик цикла-просеивания}
j:=i;
While x<a[j-l] do
begin
a[j]:=a[j-1];
Dec(j)
End;
{включение элемента}
a[j]:=x
End;
WriteLn;
For i:=l to n do
Write(a[i]:3);
ReadLn;
End.
2. Сортировка с помощью прямого выбора.
При сортировке этим методом выбирается наименьший элемент массива и меняется местами с первым. Затем выбирается наименьший среди оставшихся n - 1 элементов и меняется местами со вторым и т.д. до тех пор, пока не останется один самый больший элемент. Основной фрагмент программы может выглядеть так:
For i:=l to n-1 do
Begin
k:=i;
x:=a[i];
For j:=i+l to n do
If a[j]<x then
begin
k:=j;
x:=a[k]
End;
a[k]:=a[i];
a[i]:=x
End;

Рис. 4.4. Блок-схема алгоритма решения задачи 5 (2)
3. Сортировка с помощью прямого обмена.
Соседние элементы массива сравниваются и при необходимости меняются местами до тех пор, пока массив не будет полностью упорядочен. Повторные проходы массива сдвигают каждый раз наименьший элемент оставшейся части массива к левому его концу. Метод широко известен под названием "пузырьковая сортировка" потому, что большие элементы массива, подобно пузырькам "всплывают" на соответствующую позицию. Основной фрагмент программы содержит два вложенных цикла, причём внутренний цикл удобнее выбрать с убывающим шагом:
For i:=2 to n do
For j:=n downto i do
If a[j-1]>a[j]
then
Begin {обмен}
x:=a[j-l];
a[j-1]:=a[j];
a[j]:=x
End;

Рис. 4.5. Блок-схема алгоритма решения задачи 5 (3)






