КОНТРОЛЬНА РОБОТА з теорії ймовірностей та математичної статистики для груп ЕО, ЕФ, ЕП – 15 заоч., приск.
Пояснення. Робота містить 10 задач, з них 6 – з теорії ймовірностей, 4 – з теорії математичної статистики.
Письмовий розв’язок кожної задачі оцінюється в три бали, тобто 10 зад. х 3 бали = 30 балів.
За захист контрольної роботи під час іспиту можна отримати 10 балів. Всього 40 балів.
Номер варіанту – V визначається як порядковий номер в списку групи в деканаті або в журналі обліку відвідувань занять у старости групи.
ЗАВДАННЯ (№ 1 – № 6) з теорії ймовірностей
В завданнях №№ 1 – 6 значення V використовується для знаходження вихідних даних.
Завдання № 1 (3 бали) Пристрій складається з трьох незалежних елементів, які працюють протягом часу Т безвідмовно з ймовірностями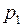 
, 
і 
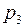. Знайти ймовірність того, що за час Т вийде з ладу:
а) тільки один елемент;
б) хоча б один елемент.
Значення параметрів обчислити за формулами
k =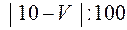 
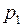= 1– k = 0,9 – k 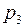=0,85 – k
Завдання №2 (3 бали) В піраміді стоїть R гвинтівок, з них L з оптичним прицілом. Стрілок, стріляючи з гвинтівки з оптичним прицілом, може вразити мішень з імовірністю 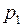, а стріляючи з гвинтівки без оптичного пристрою, – з імовірністю . Знайти ймовірність того, що стрілок вразить мішень, стріляючи із випадково взятої гвинтівки.
Значення параметрів обчислити за формулами
k =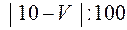
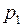= 0,95 – k/ 100 = 0,6 – k/ 100
Завдання №3 (3 бали) В піраміді стоїть R гвинтівок, з них L з оптичним прицілом. Стрілок, стріляючи з гвинтівки з оптичним прицілом, може вразити мішень з імовірністю 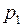, а стріляючи з гвинтівки без оптичного пристрою, – з імовірністю .Відомо, що ціль вражена. Знайти ймовірність того, що:
а) стрілок стріляв з першої гвинтівки;
б) стрілок стріляв з другої гвинтівки.
Значення параметрів беруться з попередньої задачі.
Завдання №4 (3 бали) Випадкова величина Х задана рядом розподілу
| Х | 
| 
| 
| 
|
| Р |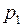
|
|
| 
|
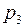
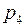
Знайти функцію розподілу та побудувати її графік. Обчислити для неї математичне сподівання, дисперсію та середньоквадратичне відхилення. Значення параметрів обчислити за формулами
R = залишок (V /4)+2
= V + 3; = + R; = + R; = +2R;
= 
; = 
; = 
; = 
.
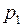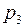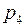Завдання №5 (3 бали) Випадкова величина задана своєю функцією розподілу 
. Знайти функцію щільності ймовірності с. Побудувати графіки 
і 
. Знайти математичне сподівання та дисперсію. Значення параметру обчислити за формулою К = 3 + V
Завдання №6 (3 бали) Випадкова величина задана нормальним розподілом з параметрами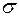 
– середньо-квадратичне відхилення: 
– математичне сподівання.
Знайти ймовірність того, що випадкова величина знаходиться в інтервалі – 
, а також, що вона відмінна від свого середнього значення за абсолютною величиною не більше ніж на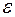 
.
Значення параметррів , , , 
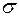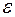визначаються за формулами
S = залишок (V /5)+1, a= V – S, b= V+2S, = V,
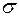= залишок (V / 8)+2, 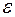=S.
