Private Sub cmdBack_Click() ' Объявление локальной процедуры
' cmdBack_Click(), которая выполняется при
' однократном нажатии на командную кнопку
' cmdBack
frmMain.Show ' Команда отображает форму frmMain на экран
Unload Me ' Команда выгружает текущую форму
End Sub ' Конец локальной процедуры
' cmdBack_Click()
Private Sub cmdEnd_Click() ' Объявление локальной процедуры
' cmdEnd_Click(), которая выполняется при
' однократном нажатии на командную кнопку
' cmdEnd
End ' Команда завершает выполнение программы
End Sub ' Конец локальной процедуры cmdEnd_Click()
Private Sub cmdRandomaze_Click() ' Объявление локальной процедуры
' cmdRandomaze_Click(), которая выполняется
' при однократном нажатии на
' командную кнопку cmdRandomaze
Call Vvod ' Вызов (запуск на выполнение)
' глобальной процедуры Vvod
Call Form_Load ' Вызов (запуск на выполнение)
' локальной процедуры Form_Load
End Sub ' Конец локальной процедуры
' cmdRandomaze_Click()
Private Sub Form_Load() ' Объявление локальной процедуры
' Form_Load(), которая выполняется
' при загрузке формы frmRezalt
grdMas.Cols = 3 'Задается общее количество столбцов
'в элементе MSFlexGrid
grdMas.Rows = N + 1 'Задается общее количество строк
'в элементе MSFlexGrid
grdMas.FixedCols = 0 'Задается общее количество фиксированных
'столбцов (окрашенных)
'в элементе MSFlexGrid
grdMas.FixedRows = 1 'Задается общее количество фиксированных
'строк (окрашенных)
'в элементе MSFlexGrid
grdMas.TextMatrix(0, 0) = "Массив" 'В ячейки с координатами (0;0)
'записываем слово Массив
grdMas.TextMatrix(0, 1) = "X" 'В ячейку с координатами (0;1)
'записываем слово Х
grdMas.TextMatrix(0, 2) = "Y" 'В ячейку с координатами (0;2)
'записываем слово Y
For k = 1 To N 'Объявление цикла для перебора
'всех элементов массива
grdMas.TextMatrix(k, 0) = k 'В ячейку з координатами (k;0)
'записываем номера элементов
grdMas.TextMatrix(k, 1) = X(k) 'В ячейку з координатами (k;1)
'записываем значения элементов
'массива Х
grdMas.TextMatrix(k, 2) = Y(k) 'В ячейку з координатами (k;2)
'записываем значения элементов
'массива Y
S = S + 2 / (X(k) + Y(k)) 'Расчет значения суммы по
'заданной формуле
Next 'Конец цикла
lblSum.Caption = "Сумма S=" + Str(S) ' Вывод значения суммы
' в элемент Label (lblSum)
End Sub ' Конец локальной процедуры Form_Load
СОДЕРЖАНИЕ ОТЧЕТА
1. Исходные данные и постановка задачи.
2. Текст кода на языке Visual Basic.
3. Подробное описание использованных свойств, методов и функций при написании программы.
4. Результаты расчета.
5. Блок-схема алгоритма программы.
Варианты заданий
1. Дан одномерный массив Y(10 + n). Найти:
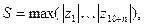 где
где 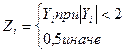 .
.
2. Вычислить значение функции:
 ,
,
где х i - заданные произвольно элементы одномерного массива размерностью (12 + n).
3. Вычислить сумму положительных элементов массива: х 1, х 2,..., х 30.
4. Вычислить среднее арифметическое элементов массива: х 1, х 2,..., х 25.
5. Вывести на печать диагональные элементы произвольно заданного двумерного массива размерностью (6 + n) X (6 + n).
6. По произвольно заданным 15-ти элементным массивам a, b, c вычислить:
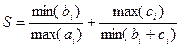 .
.
7. Подсчитать количество положительных и отрицательных элементов массива: а 1, а 2,..., а 20.
8. Найти наибольший элемент массива х 1, х 2,..., х 30 и его порядковый номер.
9. Упорядочить элементы массива а 1, а 2,..., а 25, расположив их по убыванию в том же массиве.
10. Найти наименьший элемент массива х 1, х 2,..., х 30 и его порядковый номер.
11. Вывести на печать номера элементов произвольно заданного массива А (19 + n), удовлетворяющих условию 0< A i < 9.
12. Найти наименьший из положительных элементов массива х 1, х 2,..., х 30 и его порядковый номер.
13. Определить количество четных элементов массива Х (30) и переписать их в массив Y.
14. Вывести среднее арифметическое положительных элементов произвольно заданного массива размерностью 3 X (5 + n).
15. В массиве Z (19) найти наибольший и наименьший элементы и поменять их местами.
16. Расположить элементы второй строки матрицы М (13,10) в порядке убывания.
17. Найти наибольший из отрицательных элементов массива х 1, х 2,..., х 30 и его порядковый номер.
18. Найти наименьший элемент массива V (12 + n, 9 + n) и его порядковый номер.
19. Найти сумму значений наибольшего и наименьшего элементов массива K (19 + n).
20. Переписать в массив Y в обратном порядке элементы произвольно заданного массива Z (20 + n).
21. Вывести на печать первый отрицательный элемент и его номер произвольно заданного массива размерностью 5 х (5 + n).
22. Вывести среднее арифметическое элементов произвольно заданного массива размерностью 4 х (5 + n).
23. Вычислить значение функции (х = 1,53), коэффициенты A i задать произвольно:
 .
.
24. Определить сумму квадратов максимального и минимального элементов двумерной матрицы размерностью 5 X 10. Численные значения элементов массива задать произвольно.
25. Дан строковый одномерный массив размерностью 25. Разработать программу для печати текста, образованного 11 - 15-м и 24-м элементами массива. Значения всех элементов массива задать произвольно.
26. Упорядочить элементы массива а 1, а 2,..., а 25, расположив их по возрастанию в том же массиве.
27. По произвольно заданным 15-ти элементным массивам a, b, c вычислить:
 .
.
28. Дан двумерный строковый массив размерностью 5 X 5. Составить предложение из диагональных элементов массива. Строковые значения элементов массива задать произвольно.
29. Найти наименьший из отрицательных элементов массива V (10 + n, 9 + n) и его порядковый номер.
30. Расположить элементы четвертой строки матрицы М (10, 10) в порядке возрастания.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 6
Численное решение уравнений. Редактор меню Visual Basic
ЦЕЛЬ РАБОТЫ
1. Приобретение навыков алгоритмизации и программирования численного решения уравнений.
2. Приобретение навыков создания экранных форм Visual Basic и создания на них элементов управления.
3. Приобретение навыков создания модулей и объявления глобальных переменных.
4. Приобретение навыков загрузки одних экранных форм с других.
5. Приобретение навыков создания меню.
6. Приобретение навыков работы с переключателем (OptionButton).
7. Приобретение навыков работы с рамкой (Frame).
8. Реализация алгоритма вычислительного процесса на языке Visual Basic.
СОДЕРЖАНИЕ ОТЧЕТА
1. Исходные данные и постановка задачи.
2. Текст кода на языке Visual Basic.
3. Подробное описание использованных свойств, методов, объектов и функций при написании программы.
4. Результаты расчета.
5. Блок-схема алгоритма программы.
Методические указания
Метод половинного деления. Пусть задано уравнение f(x)=0. Функция f(x) непрерывна на интервале [a,b], причем f(a)·f(b)<0, т.е. в каком-то месте этого интервала график функции пересекает ось х (знаки f(a) и f(b) разные). Значит в точке пересечения f(x) превращается в ноль и величина x в точке пересечения - это точное значение корня. Для нахождения этого корня делим отрезок [a,b] пополам. Если f ((a + b)/2) = 0, то x = (a + b) /2 является корнем уравнения. Если f ((a + b)/2) < > 0, то выбираем ту из половин [ a,(a+b)/2 или (a+b)/2, b ], на концах которой функция имеет противоположные знаки, (значит, корень находится в этой половине). Эту выбранную половину [ a,b ] снова делим пополам, опять проверяем знаки на концах, выбираем четверть отрезка [ a,b ], где знаки f(x) противоположны и т.д. При каждом разбиении пополам длину сужающегося отрезка, где ищем корень, сравниваем с заданной точностью, и, если на очередном шаге вычислений неравенство: | a–b | < ε станет справедливым, то можно считать, что решение найдено, а за приближенное значение корня принять любой из концов отрезка [a,b] (точку последнего разбиения).
Метод Ньютона (касательных). Решение алгебраических и трансцендентных уравнений по методу Ньютона применяется при условии, что на интервале [a,b], который называется интервалом отделения корня (или интервалом изоляции корня) уравнения f(x) = 0 первая и вторая производные функции f(x), т.е., f '(x) и f "(x) непрерывны и сохраняют определенные знаки (функция не имеет перегибов и экстремумов).
Процесс нахождения корня заключается в следующем. Принимается любое начальное приближение искомого значения корня внутри интервала [a,b] и заносится в рабочую ячейку х.
В этой точке вычисляется значение функции f(x 0 ) и первой производной f'(x 0 ).
Организуется цикл, в котором каждое последующее приближение корня определяется по рекуррентной формуле:
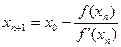
Контроль точности вычисления корня ведется по абсолютному значению разности двух соседних приближений, т.е. расчет будет продолжаться до тех пор пока:

Метод итераций (метод последовательных приближений). При использовании метода последовательных приближений исходное уравнение должно быть записано в виде: x = (x), которое называется итерационной формулой. Каким бы громоздким и сложным ни было исходное уравнение, надо разрешить его относительно одного из неизвестных, перенося все другие в правую часть итерационной формулы, причем рекомендуется выбирать то неизвестное, которое потребует наименьших преобразований для своего выделения.
Например: уравнение x 2 - sin x+ 2 x= 0 проще всего разрешить относительно третьего члена, т.е. итерационная формула будет: x = 0,5sin x -0,5 x 2.
В любых других случаях итерационная формула будет сложнее. Затем необходимо проверить сходимость итерационного процесса на интервале изоляции корня [ а,b ]. Итерационный процесс сходится, если первая производная правой части итерационной формулы в выбранном интервале по модулю меньше 1, т.е. |j’(x)| < 1.
В приведенном примере j’(x) = 0,5cos x - x, поэтому в интервале [0,1] процесс будет сходящимся. Если процесс сходится, то из интервала изоляции корня выбирается любая точка (значение x), которая принимается за начальное (нулевое) приближение искомого корня x 0. Для получения каждого следующего приближения x 1, x 2,... в правую часть итерационной формулы вместо x подставляется сначала x 0, затем полученное значение x 1, потом x 2 и т.д.:
x 1 = j(x 0)
x 2 = j(x 1)
................
xn = j(xn -1)
Каждое следующее приближенное значение корня в сходящемся процессе будет ближе к искомому истинному значению.
Повторяющиеся расчеты правой части выполняются в цикле. Контроль достижения требуемой точности производится по модулю разности между соседними приближениями и, если выполнится условие | xn +1 - xn | Ј ε, то итерационный процесс прекратится и на печать будет выдано последнее рассчитанное значение корня.
Преимуществом итерационных методов является то, что ошибки округлений и арифметических операций, выполняемых в цикле, не влияют на окончательный результат вычислений, т.к. вычислительная машина неуклонно повторяет расчеты, пока не будет достигнута заданная программой точность расчета.
Внешний вид экранных форм:
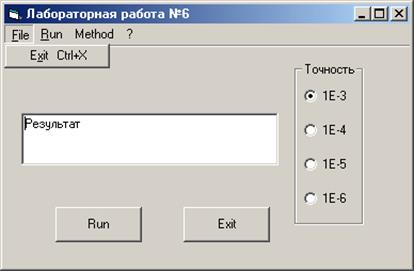

ТЕКСТ ПРОГРАММЫ
Private Sub cmdEnd_Click()
End
End Sub
Private Sub cmdStart_Click()
Call mnuPusk_Click
End Sub
Private Sub Form_Load()
If opt1(0).Value = True Then E = 0.001
If opt1(1).Value = True Then E = 0.0001
If opt1(2).Value = True Then E = 0.00001
If opt1(3).Value = True Then E = 0.000001
End Sub
Private Sub mnuDiscr_Click()
Load frmDisk
frmDisk.Show
End Sub
Private Sub mnuExit_Click()
End
End Sub
Private Sub mnuIter_Click()
mnuPolovin_delen.Checked = False
mnuNutona.Checked = False
mnuIter.Checked = True
End Sub
Private Sub mnuNutona_Click()
mnuPolovin_delen.Checked = False
mnuNutona.Checked = True
mnuIter.Checked = False
End Sub
Private Sub mnuPolovin_delen_Click()
mnuPolovin_delen.Checked = True
mnuNutona.Checked = False
mnuIter.Checked = False
End Sub
Private Sub mnuPusk_Click()
Call Form_Load
If mnuPolovin_delen.Checked = True Then
txtRez.Text = "Метод не поддерживается"
ElseIf mnuNutona.Checked = True Then
txtRez.Text = "Метод не поддерживается"
ElseIf mnuIter.Checked = True Then
X = 0.2
M1: Xn = F(X)
If Abs(X - Xn) >= E Then X = Xn: GoTo M1
txtRez.Text = "Корень уравнения х =" + Str(X)
End If
End Sub
Private Function F(X) As Single
F = 0.2 + Sin(X + 1)
End Function
Private Sub nmuAbout_Click()
Load frmAbout
frmAbout.Show
End Sub
СОДЕРЖАНИЕ ОТЧЕТА
1. Исходные данные и постановка задачи.
2. Текст кода на языке Visual Basic.
3. Подробное описание последовательности действий при написании программы.
4. Результаты расчета.
5. Блок-схема алгоритма программы.
Варианты заданий
| Вариант | Вычислить с точностью до ε = 1×10-6 | Метод |
| Корень уравнения: 2 x - ln(x + 3) = 0 | Ньютона | |
Корень уравнения:  , при а = 1000 , при а = 1000
| Простых итераций | |
Корень уравнения: 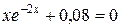 в интервале
[-1,1] в интервале
[-1,1]
| Половинного деления | |
| Вариант | Вычислить с точностью до ε = 1×10-6 | Метод |
Корень алгебраического уравнения: 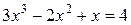 в интервале [1,2] в интервале [1,2]
| Ньютона | |
Корень трансцендентного уравнения и определить количество итераций: 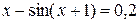
| Простых итераций | |
Корень уравнения в интервале [0,1]:
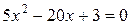
| Половинного деления | |
Решить уравнение при а = 999 и определить количество итераций: 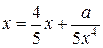
| Простых итераций | |
Решить уравнение:  , принять х = n + 1 , принять х = n + 1
| Ньютона | |
Решить уравнение: 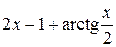
| Простых итераций | |
Корень уравнения:  в интервале [2;3], определить количество итераций в интервале [2;3], определить количество итераций
| Простых итераций | |
Вычислить в интервале [0;2] корень уравнения:
 , определить число итераций , определить число итераций
| Ньютона | |
Найти в интервале [0;1] корень уравнения:
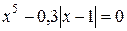
| Простых итераций | |
Найти в интервале [0;1,5] корень уравнения:
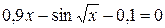
| Половинного деления | |
Решить уравнение: 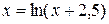
| Простых итераций | |
Найти в интервале [-1;0] корень уравнения: 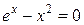
| Простых итераций | |
Найти на отрезке [0;p/4] корень уравнения: 
| Ньютона | |
Вычислить корень уравнения: 
| Простых итераций | |
Вычислить корень уравнения: 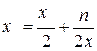
| Последовательных приближений | |
Найти на отрезке [0;p/2] корень уравнения: 
| Ньютона | |
Вычислить корень уравнения: 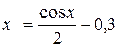
| Простых итераций | |
Корень уравнения в интервале [-1;1]: 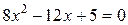
| Половинного деления | |
Вычислить корень уравнения: 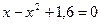
| Простых итераций | |
Корень уравнения: 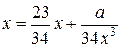 , при а = 13 , при а = 13
| Простых итераций | |
Корень уравнения: 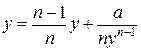 , ,
| Простых итераций | |
| Вариант | Вычислить с точностью до ε = 1×10-6 | Метод |
Корень уравнения в интервале [0;1]:

| Половинного деления | |
Корень алгебраического уравнения: 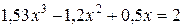 в интервале [1;1,9] в интервале [1;1,9]
| Ньютона | |
Вычислить корень уравнения: 
| Простых итераций | |
Найти на отрезке [0;p/2] корень уравнения: 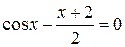
| Ньютона | |
Найти в интервале [0;1] корень уравнения:

| Половинного деления | |
Вычислить в интервале [0;1,5] корень уравнения:
 и определить число итераций и определить число итераций
| Ньютона |






