Постановка задачи
Дана схема электрической цепи, содержащая источник переменного тока, катушку индуктивности, конденсатор, набор резисторов и ключ (рис. 1).
| I2 |
| C |
| R6 |
| R5 |
| R1 |
| R2 |
| R3 |
| R4 |
| I |
| L |
| I1 |
Рис. 1
Параметры элементов цепи:
E(t)= E0(t)sin(ωt+ φ) – гармонический источник тока
E0= 15 В – амплитуда колебаний
ω= 2πƒ – циклическая частота
ƒ=40 Гц – линейная частота
φ=0 рад – фаза
t – текущее время
t0= 0 с; t1= 0,01 с; t2= 0,02 с – заданное время
T1= 0,002 с; T2= 0,008 с – заданное время для решения задачи аппроксимации и вычисления количества теплоты
R1= 30 Ом, R2= 25 Ом, R3= 50 Ом, R4= 1,88 Ом, R5= 15 Ом, R6= 50 Ом – резисторы
L= 5,57 мГн – катушка индуктивности
C= 20 мкФ – конденсатор
В начальный момент времени t= t0= 0 ключ находится в положении 1. При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю (U=0, I=0). Происходит первое переключение ключа (ключ мгновенно переводится в положение 2). При этом происходит заряд конденсатора, меняются значения U и I.
В момент времени t= t1= 0,01 c ключ мгновенно переключается в положение 1. Конденсатор разряжается, вновь меняются значения U и I. Анализ схемы заканчивается в момент t= t2= 0,02 c.
Вывод системы дифференциальных уравнений
В соответствии с рисунком запишем выражения для I и II законов Кирхгроффа для положения ключа 1:
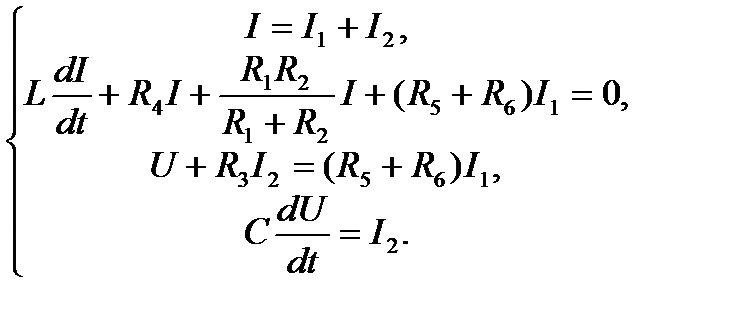 (1)
(1)
Систему (1) можно преобразовать, исключив токи I1 и I2. Тогда для величин I и U получим систему дифференциальных уравнений первого порядка:
 (2)
(2)
Аналогично может быть получена система дифференциальных уравнений для величин U и I при положении ключа 2. В этом случае им  (3)
(3)
В интервале t0≤t≤t1 решается система (3) с начальными условиями:
I(t0)= 0; U(t0)= 0. В интервале t1≤t≤t2 решается система (2). В качестве начальных условий для системы (2) I(t1), U(t1) следует использовать соответствующие значения, полученные в результате решения системы (3).
Задание на курсовую работу
1. Численная реализация решения систем дифференциальных уравнений (2) и (3):
· в пакете MathCad, используя алгоритм второй модификации метода Эйлера;
· в пакете MathCad, используя метод Рунге-Кутта;
· алгоритмически, построив блок-схему и программу на языке C++, используя алгоритм второй модификации метода Эйлера.
Сравнить результаты. При построении алгоритма и программы перевести все величины в систему СИ. На выходе первого этапа должен быть файл данных, содержащий дискретные зависимости U(t) и I(t). Шаг дискретизации (печати) должен быть таким, чтобы обеспечить не менее 40 значений величин I и U на интервале t0≤t≤t2.
2. Решение задачи аппроксимации зависимости I(t) на интервале T1≤T≤T2.
· используя пакет Excel (матричный метод, мастер диаграмм с выводом уравнения линии тренда);
· в пакете MathCad, используя алгоритм метода наименьших квадратов. На выходе второго этапа получается аналитическая формула для величины I(t).
3. Численное интегрирование. Необходимо определить количество теплоты, выделяемой на резисторе R4 за период времени T1≤T≤T2 с помощью решения интеграла:
| (4) |

где зависимость I(t) берется из результатов предыдущего этапа. Численное интегрирование проводят:
· В пакете MathCad, используя метод Симпсона.
· Написав программу на языке C++.
Сравнить результаты и оценить ошибки.
4. Сделать конструктивные выводы по результатам выполненной работы.
Решение системы дифференциальных уравнений
Численное решение системы дифференциальных уравнений в MathCad
Численное решение системы дифференциальных уравнений в среде MathCad было реализовано с помощью метода Рунге-Кутта и второй модификации метода Эйлера. В методе Рунге-Кутта использовалась встроенная функция rkfixed(). Получены графики зависимости силы тока и напряжения от времени согласно системе уравнений. При наложении графики, полученные разными методами, совпали, значит расчеты проведены верно.






