Будем предполагать, что в уравнениях Лагранжа, описывающих движение
(2.1)
все непотенциальные части обобщенных сил 
являются функциями только q и 
и не зависят явно от t.
Пусть 
— исследуемое положение равновесия. Переместим начало координат в точку 
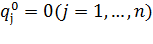, т. е. будем считать, что 
и что 
— отклонения обобщенных координат от их равновесных значений. Тогда в 2n-мерном фазовом пространстве q, положению равновесия тоже соответствует начало координат, так как при равновесии все q равны нулю.
Исследуя движения, происходящие в малой окрестности положения равновесия, мы будем считать, что во время таких движений все и 
— малые величины одного и то же порядка малости. Ограничимся в уравнениях лишь малыми первого порядка и пренебрежем малыми второго и более высоких порядков.
Чтобы сохранить в этих уравнениях лишь малые первого порядка, разложим функции Т, V и в ряды по всем независимым переменным q и и ограничимся в разложениях Т и V малыми второго порядка, а в разложении — малыми первого порядка.
В рассматриваемом стационарном случае
и чтобы сохранить в разложении Т лишь малые второго порядка, надо разложить в ряды коэффициенты 
и ограничиться в этих разложениях «нулевыми» членами, не содержащими множителей , т. е. положить
Обозначим полученные так величины через 
тогда
(2.2)
Это выражение является квадратичной формой от обобщенных скоростей с постоянными коэффициентами. Из физического смысла понятия кинетической энергии следует, что функция Т равна нулю лишь тогда, когда все одновременно равны нулю, и положительна, если хотя бы одна из отлична от нуля. Квадратичная форма, удовлетворяющая этим условиям, называется положительно определенной, а матрица, составленная из ее коэффициентов,
называется матрицей положительно определенной квадратичной формы, или просто положительно определенной матрицей.
Обратимся теперь к выражению для обобщенной силы
и разложим это выражение в ряд
(2.3)
где многоточием заменены остальные (нелинейные) члены разложения. Величина, стоящая в первой квадратной скобке, равна нулю, так как она равна значению обобщенной силы в положении равновесия
Введем обозначения
Пренебрегая в разложении (2.3) нелинейными членами и используя только что введенные обозначения, получаем
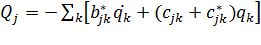(2.4)
Подставим теперь в уравнения Лагранжа (2.1) выражения (2.2) и (2.4) для Т и 
соответственно:
(2.5)
В векторно-матричной записи эта система уравнений имеет вид
(2.6)
здесь A, 
— квадратные матрицы, составленные из элементов 
соответственно, a q является n-мерным вектором-столбцом, составленным из обобщенных координат.
Линейные дифференциальные уравнения (2.5) (или (2.6)) называются уравнениями линейного приближения. Они приближенно описывают движения, происходящие в малой окрестности положения равновесия. Уравнения линейного приближения (2.5) сами по себе не определяют размеров области, в пределах которой точные нелинейные уравнения (2.1) могут быть заменены этими линейными уравнениями.
Границы этой области зависят от отброшенных нами членов высшего порядка в разложениях функций Т, V и 
. В частных случаях может оказаться, что эта область весьма велика, например, заведомо охватывает все возможные движения системы.
Вернемся к уравнениям линейного приближения (2.6). Из теории дифференциальных уравнений известно, что решение системы уравнений (2.6) имеет вид
где 
-корни уравнения
(2.7)
которое называется характеристическим уравнением линейного приближения. Каждый элемент этого определителя n-го порядка является квадратичным полиномом относительно λ; поэтому левая часть характеристического уравнения линейного приближения — характеристический полином — представляет собой полином степени m=2n.
Уравнения (2.6) отличаются от общего случая системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами только тем, что матрица А не произвольна, а всегда является матрицей положительно определенной квадратичной формы.
Выделим теперь два частных случая, когда уравнения (2.6) принимают более специальный вид.
Консервативная система. В случае консервативной системы 
, поэтому все 
и уравнения линейного приближения (2.6) сводятся к виду
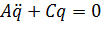(2.8)
Характеристическое уравнение (2.7) соответственно имеет вид
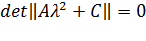(2.9)
Если дополнительно предположить, что не только А, но и С является матрицей положительно определенной квадратичной формы, то все корни характеристического уравнения (2.9) будут чисто мнимыми.
Диссипативная система. Пусть теперь 
, но зависят лишь от обобщенных скоростей. В этом случае вблизи положения равновесия
и
Разумеется, система является диссипативной не всегда, т. е. не при любом выборе чисел 
. Найдем условия, которым должны удовлетворять числа Для того, чтобы система была диссипативной. С этой целью введем квадратичную форму
(2.10)
тогда
(2.11)
Функция R называется функцией Релея.
Если рассматриваемая система диссипативна, то
где 
— мощность непотенциальных сил.
Но в силу (2.11) и теоремы Эйлера[6] об однородных функциях
и из условия 
следует, что 
, если хоть одна обобщенная скорость отлична от нуля.
Таким образом, для диссипативной системы функция Релея является положительно определенной квадратичной формой, и в уравнениях движения
будут матрицами положительно определенных квадратичных форм.
