—лучайные величины. „исловые характеристики случайной величины.
¬ычисление веро€тности событий
1. —лучайные событи€
ѕознание действительности в естественных науках происходит в результате испытаний (эксперимента, наблюдений, опыта).
»спытанием или опытом называетс€ осуществление какого-нибудь определенного комплексаусловий, который может быть воспроизведен сколь угодно большое число раз.
—лучайным называетс€ событие, которое может произойти или не произойти в результате некоторого испытани€ (опыта).
“аким образом, событие рассматриваетс€ как результат испытани€.
ѕример. Ѕросание монеты Ц это испытание. ѕо€вление орла при бросании Ц событие.
Ќаблюдаемые нами событи€ различаютс€ по степени возможности их по€влени€ и по характеру их взаимосв€зи.
—обытие называетс€ достоверным, если оно об€зательно произойдет в результате данного испытани€.
ѕример. ѕолучение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.
—обытие называетс€ невозможным, если оно не может произойти в результате данного испытани€.
ѕример. »звлечение из урны белого шара, в которой наход€тс€ лишь цветные (не белые) шары, есть событие невозможное. ќтметим, что при других услови€х опыта по€влени€ белого шара не исключаетс€; таким образом, это событие невозможно лишь в услови€х нашего опыта.
ƒалее случайные событи€ будем обозначать большими латинскими буквами A,B,C... ƒва или несколько событий называютс€ равновозможными (равносильными) в данном испытании, если имеютс€ основани€ считать, что ни одно из этих событий не €вл€етс€ более возможным или менее возможным, чем другие.
ѕример. ѕри одном бросании игральной кости по€вление 1, 2, 3, 4, 5 и 6 очков - все это событи€ равновозможные. ѕредполагаетс€, конечно, что игральна€ кость изготовлена из однородного материала и имеет правильную форму.
ƒва событи€ называютс€ несовместными в данном испытании, если по€вление одного из них исключает по€вление другого, и совместными в противном случае.
ѕример. ¬ €щике имеютс€ стандартные и нестандартные детали. Ѕерем на удачу одну деталь. ѕо€вление стандартной детали исключает по€вление нестандартной детали. Ёти событи€ несовместные.
Ќесколько событий образуют полную группу событий в данном испытании, если в результате этого испытани€ об€зательно наступит хот€ бы одно из них.
ѕример. —обыти€ из примера образуют полную группу равновозможных и попарно несовместных событий.
ƒва несовместных событи€, образующих полную группу событий в данном испытании, называютс€ противоположными событи€ми.
≈сли одно из них обозначено через A, то другое прин€то обозначать через 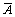 (читаетс€ Ђне Aї).
(читаетс€ Ђне Aї).
ѕример. ѕопадание и промах при одном выстреле по цели - событи€ противоположные.
„астота по€влени€ случайного событи€ - отношение m/n, числа m по€влений этого событи€ в данной последовательности испытаний к общему числу n испытаний.
ѕримеры:
1. ¬ первом €щике 10 кроликов, 1 из них белый. ¬о втором €щике тоже 10 кроликов, из них 2 белых. акова веро€тность того, что оба вслепую, наугад выбранные кролики будут белые? ќтвет: –1 = 1/10 –2= 2/10 – = –1* –2 =2/100=1/50
|
|
|
акова веро€тность того, что хот€ бы 1 кролик будет белый? – = –1+ –2 =3/10
2. акова веро€тность выпадени€ чисел Ђ5ї и Ђ6ї при двух подбрасывани€х кубика?
ќтвет: —обытие ј -----5; 6
—обытие ¬---------6;5
–ј = 1/6*1/6=1/36
–¬ = 1/6*1/6=1/36
Ќас устраивает или ј, или ¬, следовательно –(ј или ¬) = 2/36=1/18
3. »з 100 билетов 4 выигрышных.
1) акова веро€тность в первый раз выт€нуть выигрышный билет?
2) акова веро€тность во второй раз выт€нуть выигрышный билет, если в первый раз был невыигрышный?
3) акова веро€тность во второй раз выт€нуть выигрышный билет, если в первый раз был выигрышный?
ќтветы: 4/100; 4/99; 3/99
јксиомы веро€тности.
¬ теории в еро€тности формулируютс€ три аксиомы:
1. ¬еро€тность любого событи€ неотрицательна. –(ј)>=0
1. ¬еро€тность того, что произойдет хот€ бы один из возможных элементарных исходов
–=1
2. јксиома сложени€ веро€тностей.






