Метод эквивалентного генератора. Метод узловых потенциалов в обычной и матричной форме

Метод узловых потенциалов в обычной и матричной форме.

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно ,

Последовательность (алгоритм) расчета.

1) Принимают потенциал одного из узлов схемы равным нулю, а потен­циалы осталь­ных (n -1) узла считают неизвестными, подлежащими определе­нию.

2) Руководствуясь обобщенной формой, составляют (n -1) уравнение для узлов с неиз­вестными потенциалами.

3) Определяются коэффициенты узловых уравнений и составляются их матрицы.

4) Система узловых уравнений решается на ЭВМ по стандартной про­грамме для ре­шения систем линейных алгебраических уравнений с веществен­ными коэффициентами в результате чего определяются неизвестные по­тенциалы узлов j ₁, j ₂, …

5) Выбираются положительные направления токов в ветвях исходной схемы I ₁, I ₂, I ₃, I ₄, I ₅. Токи ветвей определяются из потенциальных уравнений ветвей через потенциалы узлов j ₁, j ₂, ….

6) При необходимости определяются напряжения на отдельных элемен­тах (U_k = I_kR_k), мощности источников энергии (P_Ek = E_kI_k, P_Jk = U_k J_k) и приемни­ков энергии (P_k = I_k ² × R_k).

 

8. Метод двух узлов Метод двух узлов является частным случаем метода узловых потенциалов при числе узлов в схеме n = 2

Принимаем j ₀ = 0, тогда уравнение для узла 1 по методу узловых потен­циалов будет иметь вид: j ₁ G ₁₁ = J ₁₁, откуда следует непосредственное опреде­ление напряжения между уз­лами схемы:

- уравнение метода двух узлов.

Применительно к схеме рис. 20 данное уравнение примет конкретную форму:

 

 

Метод эквивалентного генератора

Последовательность (алгоритм) расчета выгля­дит так.

1) Удаляют из сложной схемы выделенную ветвь, выполняют расчет ос­тавшейся части сложной схемы любым методом и определяют напряжение хо­лостого хода между точками подключения выделенной ветви. 2)Удаляют из сложной схемы выделенную ветвь, закорачивают в схеме точки подключения выделенной ветви, выполняют расчет оставшейся части сложной схемы любым методом и определяют ток короткого замыкания I _{кз аb} в закороченном участке между точками подключения выделенной ветви.

3)Удаляют из схемы выделенную ветвь, в оставшейся части схемы уда­ляют все источники (источники ЭДС E закорачивают, а ветви с источниками тока J удаляют из схемы), методом преобразования выполняют свертку пассив­ной схемы относительно точек подключения выделенной ветви и таким обра­зом определяют R _{вх аb} .

4) Составляют одну из эквивалентных схем замещения с генератором напряжения или с генератором тока

5) Выполняют расчет эквивалентной схемы и на­ходят искомый ток.

Так как между тремя параметрами эквивалентного генератора справед­ливо соотношение , то для их определения достаточно рассчитать любые два из трех параметров согласно п.п. 1), 2), 3), а третий параметр опре­делить из приведенного соотношения.

11. Электрические цепи синусоидального однофазного тока. В настоящее время переменный ток находит широкое применение в технике, так как он легко трансформируется и передается на большие расстояния при высоком напряжении и малых потерях. В электротехнике наибольшее распространение получил синусоидальный переменный ток, то есть ток, величина которого изменяется по закону синуса. Поэтому мгновенное значение синусоидального тока выражается формулой

где - амплитуда тока, Т - период – время, за которое совершается одно полное колебание, с; f = 1/T - частота, равная числу колебаний за 1 секунду (единица измерения частоты – Герц (Гц) или с^-1 ); ω – угловая частота (выражается в рад/с или с^-1 ).

Аргумент синуса, то есть называют фазой. Фаза характеризует состояние колебания (его численное значение) в данный момент времени t. Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой. Если частота слишком низкая, то увеличиваются габариты электрических машин и, следовательно, расход материалов на их изготовление. При слишком больших частотах увеличиваются потери энергии в сердечниках электрических машин и трансформаторах.

 

12. Среднее и действующее значения синусоидально тока синусоидально изменяющейся величины понимают её среднее значение за полпериода.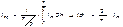

То есть среднее значение синусоидального тока составляет от амплитудного значения.

Переменный ток обычно характеризуется его действующим значением .

Значит, действующее значение синусоидального тока равно 0,707 от амплитудного

 

 

13. Представление однофазного синусоидального тока с помощью вращающихся векторов. При гармоническом изменении синусоидальной величины постоянной остаётся амплитуда. Этим можно воспользоваться для определения мгновенного значения электрической величины, не рассматривая графика её зависимости от времени. Синусоидальную функцию времени можно изобразить вектором, равным амплитуде данной функции, равномерно вращающимся с угловой скоростью ω. При этом начальное положение вектора определяется (для t=0) его начальной фазой . При изображении синусоидальной Э.Д.С., напряжений и токов из начала координат проводят векторы, равные амплитудным значениям этих величин, под углом к горизонтальной оси. Положительные углы откладываются против часовой стрелки.Если вращать вектор против часовой стрелки, то в любой момент времени он составит с горизонтальной осью угол, равный . Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины. Совокупность векторов на плоскости, изображающих Э.Д.С., напряжения, токи одной частоты, называют векторной диаграммой.При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин. С помощью векторов можно производить геометрическое суммирование электрических величин.Так, на рис. 3.4 показаны векторы токов и , а также вектор их геометрической суммы . Углы обозначают начальные фазы токов.Векторные диаграммы широко используются при анализе электрических цепей переменного тока.

 

14. Активное сопротивление, индуктивность, ёмкость цепи синусоидального тока. 1) Резистивный элемент В электрической цепи с резистивным элементом R ток изменяется по синусоидальному закону с начальной фазой ,то есть

Напряжение на зажимах резистора

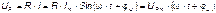
Сопротивление переменному току будет больше, чем постоянному за счет неравномерного распределения тока в проводе и потерь энергии в окружающую среду. Поэтому в отличие от сопротивления постоянному току сопротивление R в цепи переменного тока называется активным.

2) Индуктивный элемент Изменение тока в цепи с индуктивностью L (вызывает возникновение Э.Д.С. самоиндукции , которая по закону Ленца противодействует изменению тока. При увеличении тока Э.Д.С. действует навстречу току, а при уменьшении - в направлении тока, противодействуя его изменению. Показанные на рис.положительные направления и имеют место только в течение некоторого узкого промежутка времени. Для тока, изменяющегося по гармоническому закону и при L= const Э.Д.С. самоиндукции

На участке цепи с индуктивностью L напряжение опережает ток на четверть периода. На рис. 3.7в вектор напряжения опережает вектор тока i на 90⁰, а комплекс (вектор) Э.Д.С. самоиндукции находится в противофазе с комплексом напряжения индуктивное сопротивление пропорционально Если R =0, то средняя активная мощность равна 0

3) Емкостной элемент В цепи с конденсатором (рис. 3.9а), включенным на напряжение переменного тока, происходит непрерывное перемещение электрических зарядов.

Мгновенный ток в цепи равен скорости изменения заряда конденсатора:

где q – заряд конденсатора, Кл; С – ёмкость конденсатора, Ф.

Если напряжение на зажимах конденсатора изменяется по синусоидальному закону: то ток в цепи

где - амплитуда тока.

Величина, измеряемая в единицах сопротивления и обозначаемая , называется ёмкостным сопротивлением цепи:

Емкостное сопротивление обратно пропорционально частоте приложенного напряжения. Tок через конденсатор опережает по фазе напряжение на конденсаторе на 90⁰.