МЕТОДІЧНІ ВКАЗІВКИ
До лабораторних робіт
по дисципліні «Теорія алгоритмів»
(частина перша)
(для студентів напрямків підготовки «Інформатика» та «Прикладна математика»)
ЛУГАНСЬК 2011
МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ВОЛОДИМИРА ДАЛЯ
МЕТОДІЧНІ ВКАЗІВКИ
До лабораторних робіт
по дисципліні «Теорія алгоритмів»
(частина перша)
(для студентів напрямків підготовки «Інформатика» та «Прикладна математика»)
ЗАТВЕРДЖЕНО
на засіданні кафедри інформатики.
Протокол № 1 від 29.08.2008
Луганськ 2011
УДК 004(076)
Методичні вказівки до лабораторних робіт по дисципліні «Теорія алгоритмів» (для студентів спеціальностей напрямків «Інформатика» та «Прикладна математика»)/ Уклад.: Войтіков В.А. – Луганськ: вид-во СНУ ім. В.І.Даля, 2011.-**с.
Дані методичні вказівки призначені для отримання практичних навичків роботи зі існуючими структурами даних та класичними алгоритмами. У основу покладено лабораторні роботи, призначені для студентів спеціальностей напрямків «Інформатика» та «Прикладна математика». Кожна лабораторна робота надає детальну інструкцію до вправі по темі, що вивчається.
Укладачі: Войтіков В.А., ассист.
Відп. за випуск Пожидаєв В.Ф., проф.
Рецензент Нефьодов Ю.М., доцент
Лабораторна робота №1
Тема: Повне побудування алгоритму
Мета лабораторної роботи – закріплення теоретичного матеріалу, отримання практичних навичків повного побудування алгоритму.
Мета дисципліни
Мета дисципліни — навчитися
1. постановити завдання;
2. побудувати працюючий алгоритм;
3. реалізувати алгоритм як програму;
4. оценити эфективність алгоритму.
Таку мету легше сформулювати, ніж реалізувати. Світ програмування усіян набором програм, що колись вважалися готовим продуктом, але надалі виявилися неправильними, неефективними, незрозумілими або непридатними по якійсь іншій причині.
Мета першої лабораторної роботи — зробити першу спробу пояснити поняття повної побудови алгоритму, основними етапами якої є:
1. Постановка завдання.
2. Побудова моделі.
3. Розробка алгоритму.
4. Перевірка правильності алгоритму.
5. Реалізація алгоритму.
6. Анализ алгоритму та його складності.
7. Перевірка програми.
8. Формування документації.
Подальші лабораторні роботи присвячені детальному вивченню та ілюстрації цих фундаментальних етапів. Дана лабораторна робота обмежується коротким обговоренням етапів побудови алгоритмів.
Постановка завдання
Перш ніж ми зможемо зрозуміти завдання, необхідно точно його сформулювати. Це умова сама по собі не є достатньою для розуміння завдання, але вона абсолютно необхідна. Перерахуємо деякі корисні питання для погано сформульованих завдань:
1. Чи зрозуміла термінологія, що використона в попередньому формулюванні?
2. Які ісходні дані?
3. Що потрібно знайти?
4. Як визначити рішення?
5. Яких даних не вистачає і чи всі вони потрібні?
6. Чи є якісь наявні дані зайвими?
7. Які зроблені допущення?
8. І таке інше.
Приклад
Вадим— агент з продажу комп'ютерів (комівояжер); на його території 20 міст, розкиданих по всій Україні. Компанія відшкодовує йому лише 50% вартостей ділових автомобільних поїздок. Вадим обчислив, скільки йому коштуватиме переїзд на машині між кожними двома містами на його території. Він хоче понизити свої дорожні витрати.
Які ісходні дані? Вихідна інформація задана у вигляді переліку міст і відповідної матриці вартостей, т. е. двовимірного масиву з елементами ci j, що дорівнюють вартості переїзду з міста i в місто j. В даному випадку матриця вартостей має 20 рядків і 20 стовпців.
Що потрібно знайти? Ми хочемо допомогти Вадиму понизити його дорожні витрати. Це звучить декілька туманно. Дійсно, питання про те, яким буде рішення, виглядає недоречним. Обдумавши ситуацію, ми дійдемо висновку, що нічого не можемо зробити без додаткової інформації від Вадима. Чи має комівояжер в одних містах більше покупців, ніж в інших? Якщо так або якщо є якісь особливі покупці, то Вадим, можливо, захоче відвідувати якісь міста частіше. Можуть бути і такі міста, в які Вадим спеціально не поїде, а заїде туди, коли буде знаходитися в сусідньому місті. Іншими словами, нам треба знати більше про пріоритети Вадіка і враховувати переваги при складанні графіка поїздок.
Тому ми повертаємося до комівояжера і вимагаємо у нього додаткову інформацію. Він повідомляє, що хотів би мати маршрут, що починається і закінчується в його базовому місті, а також проходить по одному разу через всі останні міста. Отже, нам потрібен список міст, що містить кожне місто лише один раз, за винятком базового міста, яке стоїть в списку першим і останнім. Порядок міст в цьому списку є маршрутом, по якому Вадим повинен об'їхати задані міста. Сума вартостей проїзду між кожними двома послідовними містами списку — це загальна вартість маршруту, що представлен списком. Ми вирішимо завдання Вадима, якщо представимо йому список з найменшою можливою загальною вартістю.
Це хороша вихідна постановка завдання. Ми знаємо, що ми маємо і що хочемо знайти.
Побудова моделі
Приступаючи до розробки моделі, слід поставити принаймні два основні питання:
1. Які математичні структури можна використати для завдання?
2. Чи існують або вирішені аналогічні завдання?
У контексті моделювання друге питання часто дає відповідь на перше питання. Дійсно, більшість вирішуваних в математиці завдань, як правило, є модифікаціями раніше вирішених («Все нове придумали древні греки»). Більшість з нас не володіє талантом Ньютона, Гауса або Ейнштейна, і для просування вперед нам доводиться керуватися накопиченим досвідом.
На вибір відповідної математичної структури впливатимуть такі чинники:
1. обмеження наших знань відносно невеликою кількістю структур;
2. зручність подання;
3. простота обчислень;
4. корисність різних операцій, пов'язаних з розглянутою структурою або структурами.
Зробивши пробний вибір математичної структури, завдання слід переформулювати в термінах відповідних математичних об'єктів. Це буде одна з можливих моделей, якщо ми можемо ствердно відповісти на такі питання:
1. Чи в повному обсязі важлива інформація завдання добре описана математичними об'єктами?
2. Чи існує математична величина, яку асоціюють з шуканим результатом?
3. Чи було виявлено які-небудь корисні відносини між об'єктами моделі?
4. Чи можемо ми працювати з моделлю? Чи зручно з нею працювати?
Приклад
Повертаємося до завдання агента. Чи вирішували ми раніше аналогічні завдання?У математичному сенсі, мабуть, ні. Проте всі ми стикалися з завданнями вибору шляху по дорожніх картах або в лабіринтах. Чи можемо ми прийти до зручного поданням нашого завдання на зразок карти?
Очевидно, треба взяти аркуш паперу і нанести на ньому по одній точці, що відповідає кожному місту. Ми не будемо зображувати точки так, щоб відстань між кожною парою точок, відповідних містам i та j, було пропорційно вартості проїзду з С. Розташуємо точки будь-яким зручним способом, з'єднаємо точки i та j лініями і проставимо на них «ваги» в C.
Схема, яку тільки що було зображено, - це окремий випадок відомого в математиці графа або мережі.
Задля простоти припустимо, що у комівояжера п'ять міст.
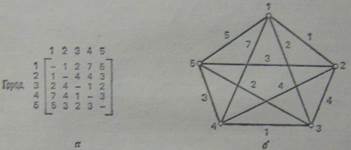
Рис. Завдання комівояжера з п'ятьма містами.
Що ми шукаємо в задачі? У термінах теорії мереж перелік міст визначає замкнутий цикл, що починається з базового міста і повертається туди ж після проходження кожного міста по одному разу. Обхід такого роду будемо називати туром. Вартість туру визначається як сума ваги усіх пройдених ребер. Завдання вирішено, якщо ми можемо знайти тур з найменшою вартістю.
Розглянута задача відома в літературі як задача комівояжера, вона стала в якійсь мірі класичною. Це один з найбільш відомих прикладів таких завдань, які дуже легко поставити і промоделювати, але дуже важко вирішити.
Розробка алгоритму
Далі необхідно познайомиться з псевдокодом, на якому ми будемо записувати алгоритми.
Псевдокод. Перелічимо основні угоди, які ми будемо використовувати.
1. Відступ від лівого поля вказує на рівень вкладеності. Це робить зайвим спеціальні команди begin та end. (У реальних мовах програмування така угода застосовується рідко, оскільки ускладнює читання програм, які переходять зі сторінки на сторінку.)
2. Цикли while, for, repeat та умовні оператори if, then, else мають таке ж значення, що і в Паскалі.
3. Символ ▷ починає коментар (йде до кінця рядка).
4. Одночасне присвоювання ije (змінні i та j одержують значення e) замінює два присвоювання je та ij (в цьому порядку).
5. Змінні локальні всередині процедури (якщо не обумовлено протилежне).
6. Індекс масиву пишеться в квадратних дужках: A[i] є i-й елемент в масиві А. Знак «..» виділяє частину масиву: A[1..j] позначає ділянку масиву А, що включає A[1], A[2], …, A[j].
7. Часто використовуються об'єкти, що складаються з декількох полів, або, як кажуть, мають кілька атрибутів. Значення поля записується як ім'я_поля [імя_об'екта]. Наприклад, довжина масиву А вважається його атрибутом і позначається length, так що довжина масиву А запишеться як length [A]. З контексту зазвичай зрозуміло, що саме позначають квадратні дужки (елемент масиву або поле об'єкта). Змінна, яка позначає масив або об'єкт, вважається покажчиком на складові його дані. Після присвоювання y x для будь-якого поля f виконано f [y] = f [x]. Більш того, якщо ми тепер виконаємо оператор f [x] 3, то буде не тільки f [x] = 3, але й f [y] = 3, оскільки у х змінні вказують на один і той же об'єкт. Покажчик може мати спеціальне значення NIL (не вказує ні на один об'єкт).
8. Параметри передаються за значенням (by value): викликана процедура отримує власну копію параметрів; зміна параметра всередині процедури зовні невидимо. При передачі об'єктів копіюється покажчик на дані, що становлять цей об'єкт, а самі поля об'єкта - ні. Наприклад, якщо х - параметр процедури, то присвоювання у х, виконане усередині процедури, зовні помітити не можна, а присвоювання f [x] 3 - можна.
Як тільки завдання чітко поставлено та для нього побудована модель, необхідно приступити до розробки алгоритму й його вирішення. Вибір методу розробки, часто сильно залежить від вибору моделі, може значною мірою вплинути на ефективність алгоритму рішення. Два різних алгоритма можуть бути правильними, але дуже сильно відрізнятися по ефективності.
Приклад.
Повернемося до комівояжеру. Постановка завдання та модель наводять на думку про наступний алгоритм.
До базового місту припишемо номер n. Усі інші пронумеруємо довільно.
Можна вирішити завдання, утворюючи всі перестановки перших n-1 цілих позитивних чисел. Для кожної перестановки будуємо відповідний тур і обчислюємо його вартість. Обробляючи таким чином всі перестановки, запам'ятовуємо тур, який до теперішнього моменту має найменшу вартість. Якщо ми знаходимо тур з більш низькою вартістю, то робимо подальші порівняння з цим туром. Даний алгоритм має назву «Вичерпний комівояжер».
Крок 0. ▷ Ініціалізація - установка в початковий стан
Set TOUR Æ; and MIN∞.
Крок 1. ▷ Утворення всіх перестановок
For I1 to (N-1)! Do
Крок 2. ▷ Отримання нової перестановки
Set PI-я перестановка цілих чисел 1, 2,..., N-1. (Зауважимо, що тут потрібен подалгорітм.)
Крок 3. ▷ Побудова нового туру
Будуємо тур Т(Р), відповідний перестановці Р; and обчислюємо вартість COST(T(P)).
(Заметим, что здесь нужны (Зауважимо, що тут потрібні два інших подалгорітма.)
Крок 4. ▷ Порівняння
if COST(T(P))<MIN then set TOURT(P); and MINCOST(T(P))
Існує тенденція: програмісти витрачають відносно невеликий час на стадію розробки алгоритму при створенні програми. Виявляється сильне бажання якомога швидше почати писати програму. Цьому спонуканню не варто піддаватися. На стадії розробки потрібне ретельне обдумування, слід також приділити увагу і іншим етапам. Перші три етапи впливають на наступні, а шостий і сьомий етапи забезпечують цінну зворотний зв'язок, який може змусити нас переглянути деякі з попередніх етапів.
Правильність алгоритму.
Доказ правильності алгоритму - це один з найбільш важких, а іноді і особливо утомливих етапів створення алгоритму.
Ймовірно, найбільш поширена процедура докази правильності програми - це прогон її на різних тестах. Якщо видані програмою відповіді можуть бути підтверджені відомими або обчисленими вручну даними, виникає спокуса зробити висновок, що програма «працює». Однак цей метод рідко виключає всі сумніви, може існувати випадок, в якому програма не спрацює.
Розглянемо таку загальну методику докази правильності алгоритму. Припустимо, що алгоритм описаний у вигляді послідовності кроків від кроку 0 до кроку m. Постараємося запропонувати деяке обгрунтування правомірності для кожного кроку. Затем постараемся предложить доказательство конечности алгоритма, при этом будут проверены все подходящие входные данные и получены все подходящие выходные данные. Потім постараємося запропонувати доказ кінцівки алгоритму, при цьому будуть перевірені всі підходящі вхідні дані і отримані всі відповідні вихідні дані.
Приклад.
Алгоритм «Вичерпний комівояжер» настільки простий, що його правильність легко довести. Оскільки перевіряється кожен тур, повинен бути перевірений і тур з мінімальною вартістю; як тільки до нього дійде черга, його буде зафіксовано. Він не буде відкинутий - це може статися лише в тому випадку, якщо існує тур з меншою вартістю. Алгоритм повинен закінчити роботу, оскільки кількість турів, які потрібно перевірити, звичайно. Такий метод доказу відомий як «доказ вичерпуванням»; це самий грубий з усіх методів доказу.
Підкреслимо той факт, що правильність алгоритму ще нічого не говорить про його ефективність. Вичерпні алгоритми рідко бувають хорошими в усіх відношеннях.
Реалізація алгоритму.
Конкретна реалізація може істотно впливати на вимоги до пам'яті та швидкість алгоритму. Щоб вибрати реалізацію правильно, необхідно відповісти, наприклад, на такі питання:
9. Які основні змінні?
10. Яких вони типів?
11. Скільки потрібно масивів і який розмірності?
12. Чи має сенс користуватися пов'язаними списками?
13. Які потрібні підпрограми (можливо, вже існуючі)?
14. Якою мовою програмування користуватися?
Другий, але не менш важливий етап побудови програмної реалізації - це програмування зверху-вниз. Цей підхід до розробки і реалізації полягає в перетворенні алгоритму в таку послідовність все більш конкретизованих алгоритмів, що остаточний варіант являє собою програму.
Аналіз алгоритму і його складності.
Аналіз алгоритму та його складності необхідний для отримання оцінок і кордонів, для обсягу пам'яті або часу роботи, який буде потрібно алгоритму для успішної обробки конкретних даних.
Також аналіз алгоритмів необхідний для отримання кількісного критерію для порівняння двох алгоритмів, що претендують на вирішення однієї і тієї ж задачі.
Нехай А - алгоритм для рішення деякого класу задач, а n-розмірність окремої задачі цього класу. Визначимо функцію fА(n) як робочу функцію, що дає верхню межу для максимального числа основних операцій (додавання, порівняння і т. п.), які повинен виконати алгоритм А для вирішення завдання розмірності n. Кажуть, що алгоритм А поліноміальний, якщо fА(n) росте не швидше, ніж поліном від n, інакше алгоритм А експонентний. Цей критерій заснований на часі в гіршому випадку, але аналогічний критерій може бути також визначений для середнього часу роботи. Сучасні комп'ютери досить добре сприймають поліноміальні алгоритми для великих завдань, а на експоненціальних алгоритмах швидко «задихаються».
Функцію f(n) визначають як О[g(n)] і говорять, що вона порядку g (n) для великих n, якщо
при n®∞ lim(f(n) / g(n))=constant¹0
Це позначається, як f(n) = O[g(n)]. Функція h(n) є o[z(n)] для великих n, якщо
при n®∞ lim(h(n) / z(n))=0
Ці символи вимовляються відповідно, як «О велике» та «о мале». Інтуїтивно, якщо f(n) є O[g(n)], то ці дві функції, по суті, зростають з однаковою швидкістю при n®∞. Якщо f(n) є o[g(n)], то g(n) зростає набагато швидше, ніж f(n).
Приклад.
a) поліном f(n)=2n5+6n4+6n2+18 є O(n5), тому що
при n®∞ lim((2n5+6n4+6n2+18)/n5)=2
він являє собою o(n5,1), o(en) и o(2n). Дійсно, він є «о малим» від будь-якої функції, зростаючої швидше, ніж поліном п'ятого ступеня.
b) Функція f (n) = 2 nє o (n!), тому що
при n®∞ lim (2n / n!)=0
Однак, 2n є O(2n+1) та o(5n-1)
c) Функція f(n)= 1000*n^(1/2) є o(n).
Загальні коефіцієнти fА(n) у загальному випадку залежать від реалізації; характеристика O(n2) зазвичай властива алгоритму, тобто не залежить від різних особливостей реалізації.
Відомо досить велика безліч завдань для вирішення яких існують тільки експоненціальні алгоритми. У таких випадках необхідно використовувати лише найбільш ефективні з них. Очевидно, що алгоритм вирішує задачу розмірності n за O(n2) переважно алгоритму, що вирішує її за O(n!) або O(nn) кроків.
Приклад.
Розглянемо раніше розглянутий алгоритм (вичерпний комівояжер). Відразу можна зробити висновок, що це експонентний алгоритм з оцінкою принаймні O(n!). Навіть якщо потрібна тільки один крок для кожної перестановки, ця частина алгоритму зажадає O[(n-1)!] кроків. Як тільки отримана перестановка, можна знайти відповідний тур і його вартість за O(n) кроків. Тому будь-яка верхня межа для загального часу роботи повинна бути принаймні O(n!).
Припустимо, що у нашого комівояжера 20 міст і що у нас є феноменальний подалгорітм, який генерує нову перестановку за один крок. Припустимо також, що ми маємо швидкодіючу машину, яка виконує кожен елементарний крок (наприклад, порівняння, додавання, пошук елемента матриці) за 10-10 сек. Тоді, так як 20!»2*1018, рішення нашої задачі з використанням запропонованого алгоритму займе від 6 до 7 років.
Цей приклад сильно підриває нашу довіру до запропонованого алгоритму. На наступних парах ми розглянемо, як можна отримати алгоритми для відшукання стерпних, але не обов'язково оптимальних рішень для великих завдань за прийнятний час.
Перевірка програми.
Програма повинна бути перевірена, для широкого спектру допустимих вхідних даних.
Як вибрати вхідні дані для тестування? На це питання неможливо дати загальної відповіді. Для будь-якого алгоритму відповідь залежить від складності програми, наявного ресурсу часу, варіантів вхідних даних та їх кількості. Зазвичай множена всіх входів величезна, і повна перевірка практично неможлива.Необхідно вибрати безліч входів, які перевіряють кожну ділянку програми.
Досвід показує. Що аналіз середнього функціонування алгоритму більш цінний і трудомісткий, ніж аналіз найкращого і найгіршого випадків.
Аналітичний і експериментальний аналіз доповнюють один одного. Аналітичний аналіз може бути неточним, якщо зроблені занадто сильні спрощують допущення. У цьому випадку можуть бути отримані тільки грубі оцінки. З іншого боку, отримати достатнє експериментальне підтвердження для гарантій будь-якої статистичної достовірності може виявитися неможливим або непрактичним. Експериментальні результати, особливо коли використовуються випадково згенеровані дані, можуть виявитися занадто однобокими. Щоб отримати достовірні результати, потрібно там, де це можливо, провести як аналітичне, так і експериментальне дослідження.
Бажано, використовуючи аналітичні та експериментальні методи, прагнути до визначення тих вхідних даних, які вважаються або «хорошими», або «поганими». Це дозволить обмежити випадки експоненціального вибуху в тій ситуації, коли алгоритм поліноміальний або експонентний в залежності від вхідних даних.
Документація.
Золоте правило: «Оформляйте ваші програми в такому вигляді, в якому вам хотілося б бачити програми, написані іншими».
Не варто розуміти під документацією лише коментарі. Документація включає в себе всю інформацію і допомагає пояснити, що робиться в програмі. Зокрема, блок-схеми, описи ступенів у вашому побудові зверху-вниз, допоміжні докази правильності, результати тестування, детальні описи формату і вимог до введення/виводу і таке інше.
Завдання для виконання лабораторної роботи №1.
Провесті повну побудову алгоритмів вирішення наступних завдань:
1. Написати функцію визначення найбільшого числа з усіх чисел одновимірного масиву.
2. Написати процедуру визначення суми позитивних чисел одновимірного масиву, суми негативних, а також кількості нульових елементів.
3. Написати функцію отримання суми чисел одновимірного масиву, а також, номер і значення мінімального числа масиву.
4. Написати логічну функцію визначення приналежності числа А інтервалу [В; С].
5. Написати процедуру виведення цілого числа N прописом (0 <N <99).
6. Написати функцію отримання дня тижня за його номером.
7. Написати функцію отримання кількості чисел одновимірного масиву, що належать проміжку [А, В].
8. Написати процедуру отримання скалярного добутку двох векторів.
9. Написати логічну функцію порівняння 2-х дат, кожна з яких задана трьома числами: числом, місяцем та роком.
10. Написати функцію визначення кількості повних років між двома датами, кожна з яких задана трьома числами: числом, місяцем та роком.
11. Написати процедуру отримання коренів квадратного рівняння, заданого своїми коефіцієнтами.
12. Написати процедуру, яка для трьох довільних чисел X, Y, Z шляхом перезапису значень видає впорядковану трійку: X = Y = Z.
13. Написати логічну функцію визначення: чи є задане ціле число точним квадратом. Додатково функція повинна видати ціле значення кореня квадратного цього числа.
14. Дано натуральне число N. Написати процедуру знаходження серед чисел 1,2,..., N таких, які можна представити у вигляді суми квадратів двох натуральних чисел.
15. Дано натуральне число N. З'ясувати, чи є серед чисел N, N +1, N +2,...., 2N "близнюки", тобто прості числа, різниця між якими дорівнює двом. Написати процедуру, що розпізнає прості числа.
16. Написати програму, що містить процедуру, за допомогою якої можна визначити суму цифр кожного з чисел, що вводяться. Закінченням ввести послідовність є число 0.
17. Дани 3 матриці цілих чисел, кожна розмірністю N * N. Перевірити симетричність відносно головної діагоналі для кожної матриці.
18. Дани 3 матриці цілих чисел, кожна розмірністю 2 * N. Для кожної матриці обчислити і віддрукувати добуток двох елементів кожного стовпця, припиняючи процес при виявленні негативного добутку.
19. Дани 3 матриці цілих чисел, кожна розмірністю 2 * N. Для кожної матриці обчислити і віддрукувати номери тих стовпців, сума елементів яких меньш нуля.
20. Дани 3 матриці цілих чисел, кожна розмірністю 2 * N. Для кожної матриці обчислити і віддрукувати добуток двох елементів кожного стовпця, починаючи з першого і припинити процес, як тільки буде виявлено рівність першого і другого елементів в будь-якому стовпці.
21. Дани 3 матриці цілих чисел, кожна розмірністю 2 * N. Для кожної матриці обчислити і віддрукувати номери тих стовпців, в яких обидва елементи мають нульові значення.
22. Написати процедуру знаходження найбільшого спільного дільника для М позитивних чисел.
23. Дани два масиви: А розмірністю N та В розмірністю М, причому
А1£А2£А3£...£Аn
B1£B2£B3£...£Bm
Побудувати вектор З розмірністю М + N (використовуючи процедуру), в якому:
С1£С2£С3£...£Сn+m
24. Обчислити кількість слів в рядку.
25. Визначити найдовше слово в рядку.
26. Сформувати новий рядок, замінивши у вхідному рядку кожну послідовність пробілів на один пробіл.
27. Сформувати новий рядок видаливши з вхідного цифри.
28. Визначити чи є рядок послідовністю цілих чисел.
29. Обчислити значення цілого числа за його літерному поданням.
30. В рядку тексту програми на Паскалі видалити коментарі.
Вимоги до звіту:
Звіт з лабораторної роботи повинен відповідати наступній структурі:
1. Словесна постановка задачі. У цьому підрозділі проводиться повний опис завдання. Описується суть завдання, аналіз вхідних в неї фізичних величин, район їх допустимих значень, одиниці їх вимірювання, можливі обмеження, аналіз умов при яких завдання має рішення (не має рішення), аналіз очікуваних результатів.
2. Математична модель. У цьому підрозділі вводяться математичні описи фізичних величин і математичний опис їх взаємодій. Мета підрозділу - представити вирішувану задачу в математичній формулюванні.
3. Алгоритм рішення задачі. У підрозділі описується розробка структури алгоритму, обгрунтовується абстракція даних, завдання розбивається на підзадачі. Приводится схема алгоритму або псевдокод. Вказується оцінка алгоритму.
4. Лістинг програми.
5. Контрольний тест. Підрозділ містить набори вихідних даних і отримані в ході виконання програми результати.
6. Висновки з лабораторної роботи.
Лабораторна робота №2
Тема: Графи. Структури даних.
Мета лабораторної роботи – закріплення теоретичного матеріалу, отримання практичних навичків роботи з графами та аргументованого вибіру структур даних для вирішення завдань.
Графи.
На лекції, ми розглянули поняття граф і маємо про нього уявлення. Важливо усвідомлювати, що граф може бути представлений багатьма способами. Наприклад, графи на наступному малюнку це одна і та ж неорієнтована мережа.
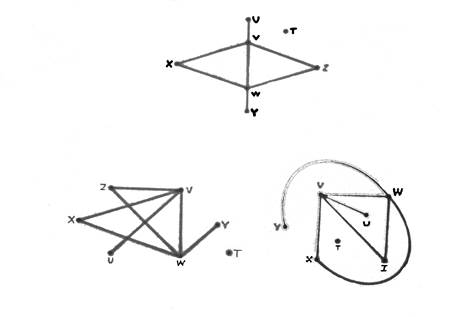
Рис. 1 Способи зображення заданої неорієнтованої мережі
Представлення графів.
1. Матріца суміжності.
2. Матріца інцидентності (стовпець іменується іменами ребер, рядки іменами вершин. Кожен стовпець містить рівно дві одиниці. Ідентичних стовпців немає.)
3. Вектори суміжності - матриця, в якій елементи відповідають безпосередньо міткам, що приписані вершинам графу. У такій матриці i-й рядок містить вектор, компонентами якого є всі вершини, суміжні з i-ю вершиною. Вектори суміжності особливо добре визначають мережу, коли завдання може бути вирішена за невелику кількість переглядів кожного ребра в заданому графі.
4. Спіскі суміжності Означене представлення розглянемо трохи пізніше. (на лекції)
Ізоморфізм.
Остовне дерево для графа є остовна підмережа, що є деревом.
Граф зв'язний тоді й тільки тоді, коли він містить остовне дерево.
Розглянемо наступну задачу. У нас є два подання графу. Як дізнатися, чи не описують вони одну й ту ж мережу?
Два графа G1 і G2 ізоморфні, якщо існує взаємно-однозначна відповідність між вершинами G1 і G2, таке, що дві вершини В1 і В2 суміжні в G1 тоді і тільки тоді, коли в G2 суміжні відповідні їм вершини.
Проблема визначення, чи є дві мережі ізоморфними, несподівано виявляється важкою. Для довільних мереж всі відомі алгоритми, що гарантують правильну відповідь, експоненціальні.
Фактично навіть для невеликих мереж цю задачу вирішити нелегко. Всі три мережі на наступному малюнку ізоморфні одна одній.
 |
Якщо вам це здається очевидним, спробуйте визначити, які мережі ізоморфні одна одній (якщо такі є) з наведених на наступному рисунку.
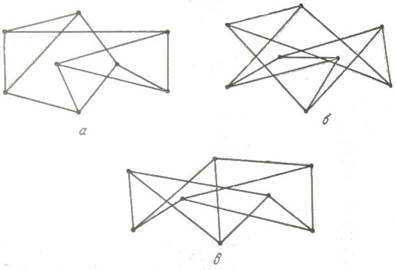
Розглянемо, наприклад, два графа G1 і G2: у кожного 10 вершин і кожна має 3 ступень. Будь-яка з можливих взаємно однозначних функцій h з V1 у V2 буде задовольняти вказаним вище обмеження на ступінь; є 10! таких функцій. Тому для вирішення питання про ізоморфності G1 і G2 нам потрібно було б випробувати кожну з 10! можливих функцій, щоб знайти одну, яка задовольняє вимогу ізоморфізму.
Перед обличчям цього комбінаторного вибуху дослідники часто відмовляються від пошуку ефективного алгоритму і замість цього будують прості процедури, від яких очікується хороша робота в більшості випадків.
Інваріантом графа G називається параметр, що має одне і теж значення для всіх мереж, ізоморфних G. Наприклад:
1. Чісло вершин.
2. Число ребер.
3. Чісло компонент.
4. Последовательность ступенів.
Евристичний алгоритм має такі властивості:
1. Він, як правило, знаходить хороші, хоча і не обов'язково оптимальні, рішення.
2. Его легше і швидше реалізувати, ніж будь-який з відомих точних алгоритмів (тобто алгоритмів гарантують оптимальне рішення.)
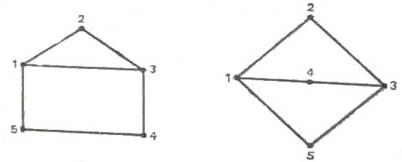
Евристики для вирішення завдань ізоморфізму зазвичай спрямовані на доказ того, що графи не ізоморфні. Зараз не відома множина інваріантів, яка дозволила б за поліноміальний час показати, що графи ізоморфні. Розгляд більшого числа інваріантів збільшує ймовірність правильного висновку про ізоморфізми при збігу всіх значень параметрів, але в загальному випадку нічого не гарантує. Наприклад, для двох пятівершінних графів представлених на рисунку всі чотири з перерахованих вище інваріантів збігаються, але ці мережі не ізоморфні.
 |
Алгоритм «Порівняння порядків суміжності».
Розглянемо приклад досить складною евристики, що працює з матрицею суміжності A (G). Сама по собі матриця суміжності не є інваріантом, хоча якщо G і G1 ізоморфні, то при деякому переупорядочивания стовпців і рядків A (G) ми отримуємо A (G1). Якщо у мереж G і G1 M вершин, то пошук потрібної послідовності перестановок рядків і стовпців вимагає в гіршому випадку O(М!) операцій. Втім, описувана нижче поліноміальна процедура справляється начебто досить добре із завданням відсіювання неізоморфних графів.
Обчислюється A2 (Gi) для i = 1, 2. потім переставляються терміни та стовпці A2 (G1) і A2 (G2) так, щоб елементи на головній діагоналі опинилися в спадному порядку. Якщо G1 і G2 ізоморфні і все діагональні елементи різні, то при цій перестановці повинні вийти ідентичні матриці. Якщо ні, то дані два графа не можуть бути ізоморфними. Якщо матриці ідентичні, можна продовжити перевірку зведенням в наступну ступінь, якщо всі з перевірених матриць співпадають, то вельми правдоподібно, але не обов'язково істинно, що графи ізоморфні.
Завдання для виконання лабораторної роботи №2.
Розробіть, реалізуйте і перевірте евристичні алгоритми для вирішення наступних завдань:
1. Виявлення ізоморфізму. Обмежитися графами не більше ніж з 12 вершинами.
2. Обчислити кількість розділяючих вершин в даному графі.
3. Перетворення матриці суміжності у матрицю інцидентності.
4. Обчислити кількість мостів в даному графі.
5. Перетворення матриці інцидентності у матрицю суміжності.
6. Обчислити кількість листів заданого графу.
7. Обчислити кількість зв'язкових компонент графа.
8. Обчислиті кількість залежних вершин для кожної вершини.
9. Обчислити ступінь схожості двох заданих графів.
10. Визначити зв’язність заданого графу.
11. Обчислити кількість зв’язних компонент заданого графу.
12. Перетворення матриці суміжності у вектори суміжності.
13. Перетворення векторів суміжності у матрицю інцидентності.
14. Перетворення матриці інцидентності у вектори суміжності.
15. Перетворення векторів суміжності у матрицю суміжності.
16. Пошук мінімальної відстані між двома заданими вершинами.
17. Пошук мінімальної відстані між вказаною та іншими вершинами.
18. Рішення завдання комівояжеру.
19. Перевірка, чи є граф деревом.
20. Перевести граф з виду матриці суміжності в вид списків суміжності.
21. Реалізувати додавання ребра в граф, представлений списком суміжності.
22. Перевести граф з виду списків суміжності в вигляд матриці суміжності. Реалізувати додавання ребра в граф, представлений списком суміжності.
23. Перевести граф з виду матриці суміжності в вид списків суміжності. Реалізувати видалення ребра з графа, представленого списком суміжності.
24. Перевірити, чи є граф двочастковим.
Вимоги до звіту:
Звіт з лабораторної роботи повинен відповідати наступній структурі:
1. Словесна постановка задачі. У цьому підрозділі проводиться повний опис завдання. Описується суть завдання, аналіз вхідних в неї фізичних величин, район їх допустимих значень, одиниці їх вимірювання, можливі обмеження, аналіз умов при яких завдання має рішення (не має рішення), аналіз очікуваних результатів.
2. Математична модель. У цьому підрозділі вводяться математичні описи фізичних величин і математичний опис їх взаємодій. Мета підрозділу - представити вирішувану задачу в математичній формулюванні.
3. Алгоритм рішення задачі. У підрозділі описується розробка структури алгоритму, обгрунтовується абстракція даних, завдання розбивається на підзадачі. Приводится схема алгоритму або псевдокод. Вказується оцінка алгоритму.
4. Лістинг програми.
5. Контрольний тест. Підрозділ містить набори вихідних даних і отримані в ході виконання програми результати.
6. Висновки з лабораторної роботи.
Лабораторна робота №3
Тема: Структури даних.
Мета лабораторної роботи – закріплення теоретичного матеріалу, отримання практичних навичків роботи та аргументованого вибіру структур даних для вирішення завдань.
Лінейний список - це кінцева послідовність однотипних елементів (вузлів), можливо, з повтореннями. Кількість елементів у послідовності називається довжиною списку, причому довжина в процесі роботи програми може змінюватися.
При пов'язаному зберіганні як елементи збереження використовуються структури, пов'язані з однією з компонент в ланцюжок, на початок якої (першу структуру) вказує покажчик head. Структура, що утворює елемент зберігання, повинна крім відповідного елемента списку містити і покажчик на сусідній елемент зберігання.
Перша структура зазвичай називається «головою» списку, остання структура в списку називається «хвостом» списку.
Опис структури і покажчика може мати вигляд:
typedef struct TNode / * структура елемента зберігання * /
{
float val; / * дані, що зберігаються у вузлі * /
TNode * n; / * покажчик на наступний елемент зберігання * /
}
Схематично список подається наступним чином:

Види списків:
1. однонаправлений;
2. двунаправлений;
3. циклічний;
Однонаправлений список складається з елементів, кожен з яких вказує на наступний.
Графічне подання:

Двонаправлений список складається з елементів, кожен з яких вказує на наступний і на попередній елементи.
Графічне подання:
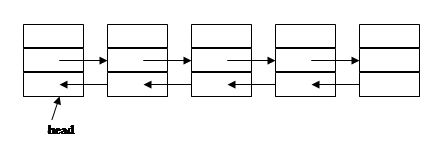
Циклічний список відрізняється від односпрямованого тим, що останній елемент у ньому вказує на голову списку.
Графічне подання:
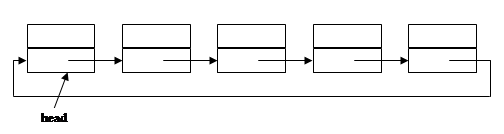
Завдання для виконання лабораторної роботи №3.
З використанням структур та динамічної пам'яті реалізувати односпрямований список. Описати і реалізувати функції для запису списку у файл і читання його з файлу.
Списки, які повертаються як результат роботи функцій створювати динамічно з обов'язковим подальшим коректним видаленням.
1. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) підрахунок рядків у списку;
b) отримання j-го символу i-го рядка (якщо такого не існує, повернути 0);
c) обмін місцями i-й і j-й рядків;
d) заміна i-го рядка копією j-й;
2. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) додавання після i-го рядку копії j-го рядку;
b) видалення j-го рядку зі списку;
c) пошук входження символу С в текст, що знаходиться в списку, з поверненням його координат i (рядок) та j (стовпець);
d) пошук рядка з найбільшою кількістю входжень символу С.
3. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати такі дії:
a) перевірка, чи порожній список;
b) підрахунок середнього арифметичного елементів непорожнього списку;
c) заміна в списку всіх входжень E1 на Е2;
d) обмін місцями першого і останнього елементів.
4. Тип даних, що зберігаються у списку: символ. Реалізувати такі дії:
a) перевірка, чи порожній список;
b) упорядкування елементів списку за алфавітом;
c) заміна в списку всіх входжень E1 на Е2;
d) заміна в списку всіх символів в нижньому регістрі на символи у верхньому регістрі.
5. Тип даних, що зберігаються у списку: рядок із десяти символів. Реалізувати такі дії:
a) підрахунок кількості слів, що починаються і закінчуються таким самим символом;
b) підрахунок кількості слів, що починаються з того ж символу, що й наступне слово;
c) підрахунок кількості слів, які збігаються з останнім словом;
d) пошук в списку заданого слова (повернути номер елемента списку).
6. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) перевірка, чи порожній список;
b) створення нового списку, до якого входять лише рядки, що починаються з символу у верхньому регістрі;
c) пошук рядка, що містить заданий підрядок;
d) обмін місцями першого і останнього елементів.
7. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати такі дії:
a) видалення зі списку першого входження заданого елемента;
b) створення нового списку, до якого входять тільки позитивні значення;
c) створення нового списку, до якого входять лише значення, які менше заданого порогу;
d) порівняння двох списків на рівність їх елементів.
8. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) вставка нового елемента в початок списку;
b) вставка нового елемента перед першим елементом, що не перевершує заданого (при вставці нових елементів до списку лише таким способом вийде впорядкований список);
c) пошук рядка, що містить задане слово;
d) обмін місцями першого і останнього елементів списку.
9. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) додавання в список нового елемента Е1 перед першим входженням елемента Е, якщо Е входить в список;
b) додавання в непорожній список пари нових елементів Е1 і Е2 перед його останнім елементом;
c) перенесення в початок непорожнього списку його останнього елемента;
d) заміна початкового символу кожного рядка символом верхнього регістру.
10. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) видалення з непорожнього списку першого елемента;
b) видалення з непорожнього списку елемент з заданим номером;
c) створення нового списку з елементів, що містять заданий підрядок;
d) заміна початкового символу кожного рядка символом нижнього регістру.
11. Тип даних, що зберігаються у списку: ціле число. Реалізувати такі дії:
a) сортування чисел в порядку їх зростання;
b) відображення номерів найбільших чисел послідовності на екрані;
c) збільшення усіх чисел послідовності на задану величину;
d) переміщення початкового елементу списку у кінець списку.
12. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) порівняння двох списків;
b) створення копії списку;
c) перевірка, чи є в списку хоча б два однакових елемента;
d) створення нового списку з рядків, що не містять заданий підрядок.
13. Тип даних, що зберігаються у списку: символ. Реалізувати такі дії:
a) додавання в кінець списку L1 всіх елементів списку L2;
b) вставка в список L1 за першим входженням елемента Е всіх елементів списку L2, якщо Е входить в L1;
c) перевірка, чи є в списку хоча б два однакових елемента;
d) заміна групи рівних елементів, що йдуть підряд, на один.
14. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати використовуючи рекурсію наступні дії:
a) визначення, чи входить елемент в список;
b) підрахунок кільеості входжень елемента в список;
c) пошук максимального елемента списку;
d) заміна у списку усіх входжень E1 на E2.
15. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати використовуючи рекурсію наступні дії:
a) видалення зі списку всіх входжень елемента Е;
b) створення нового списку, що складається зі зворотних значень елементів вихідного списку;
c) подвоєння кожного входження заданого елемента в список;
d) заміна групи входжень однакових елементів одним першим входженням.
16. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) видалення останнього символу рядка, якщо це знак, у всіх елементах списку;
b) створення нового списку з усіх елементів списку, які перебувають перед заданим елементом (елемент задається рядком). Якщо такого елементу немає, результат - копія вихідного списку;
c) перевірка, чи є в списку хоча б два однакових елемента;
d) видалення усіх елементів списку в яких присутній заданий підрядок.
17. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати такі дії:
a) створення нового списку з елементів входять хоча б в один із списків L1 і L2;
b) вставка нового елемента перед заданим;
c) перевірка, чи є в списку хоча б два однакових елемента;
d) перенесення останнього елемента списку в його початок.
18. Тип даних, що зберігаються у списку: число з плаваючою крапкою. Реалізувати такі дії:
a) розподіл всіх елементів списку на задане значення;
b) створення нового списку з усіх елементів, які входять тільки в один зі списків L1 і L2;
c) перевірка, чи є елементи списку арифметичною прогресією;
d) перенесення заданого елемента у кінець списку (елемент задається номером).
19. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) заміна знаків пунктуації на прогалини;
b) створення нового списку з усіх елементів списку, які завершуються крапкою;
c) підрахунок кількості входжень заданого символу у рядки списку;
d) видалення всіх рядків довше заданої межі.
20. Тип даних, що зберігаються у списку: рядок змінної довжини. Реалізувати такі дії:
a) обмін вмістом двох заданих елементів списку;
b) створення нового списку з усіх елементів списку, які перебувають після заданого елемента (елемент задається номером позиції). Якщо такого елементу немає, результат - порожній список;
c) підрахунок кількості символів у всіх рядках списку;
d) пошук позиції найдовшого рядку.
Вимоги до звіту:
Звіт з лабораторної роботи повинен відповідати наступній структурі:
1. Словесна постановка задачі. У цьому підрозділі проводиться повний опис завдання. Описується суть завдання, аналіз вхідних в неї фізичних величин, район їх допустимих значень, одиниці їх вимірювання, можливі обмеження, аналіз умов при яких завдання має рішення (не має рішення), аналіз очікуваних результатів.
2. Математична модель. У цьому підрозділі вводяться математичні описи фізичних величин і математичний опис їх взаємодій. Мета підрозділу - представити вирішувану задачу в математичній формулюванні.
3. Алгоритм рішення задачі. У підрозділі описується розробка структури алгоритму, обгрунтовується абстракція даних, завдання розбивається на підзадачі. Приводится схема алгоритму або псевдокод. Вказується оцінка алгоритму.
4. Лістинг програми.
5. Контрольний тест. Підрозділ містить набори вихідних даних і отримані в ході виконання програми результати.
6. Висновки з лабораторної роботи.
Лабораторна робота №4
Тема: Алгоритми та їх складність.
Мета лабораторної роботи – закріплення теоретичного матеріалу, отримання практичних навичків визначення складності алгоритмів.
Аналіз алгоритмів та їх складності частково розглянено в першій лабораторній роботі.
Оцінка програм
Для більшості проблем існує багато різних алгоритмів. Який з них вибрати для вирішення конкретного завдання? Це питання дуже ретельно опрацьовується в програмуванні. Ефективність програми (коду) є дуже важливою її характеристикою. Користувач завжди віддає перевагу більш ефективним рішенням навіть у тих випадках, коли ефективність не є вирішальним фактором. Ефективність програми має дві складові: пам'ять (або простір) і час.
Просторова ефективність вимірюється кількістю пам'яті, необхідної для виконання програми.
Комп'ютери мають обмежений обсяг пам'яті. Якщо дві програми реалізують ідентичні функції, то та, яка використовує менший обсяг пам'яті, характеризується більшою просторової ефективністю. Іноді пам'ять стає домінуючим чинником в оцінці ефективності програм. Однак в останні роки у зв'язку з швидким її здешевленням ця складова ефективності поступово втрачає своє значення. Часова ефективність програми визначається часом, необхідним для її виконання.
Кращий спосіб порівняння ефективностей алгоритмів полягає в зіставленні їх порядків складності. Цей метод можна застосовувати як до часової, так і просторової складності. Порядок складності алгоритму виражає його ефективність зазвичай через кількість оброблюваних даних.
Наприклад, певний алгоритм може істотно залежати від розміру оброблюваного масиву. Якщо, скажімо, час обробки подвоюється з подвоєнням розміру масиву, то порядок тимчасової складності алгоритму визначається як розмір масиву.
Порядок алгоритму - це функція, домінуюча над точним виразом часової складності.
Існують три важливі правила для визначення складності.
1. O (k * f) = O (f)
2. O (f * g) = O (f) * O (g) або O (f / g) = O (f) / O (g)
3. O (f + g) дорівнює домінанту O (f) і O (g)
тут k позначає константу, a f та g - функції.
Перше правило декларує, що постійні множники не мають значення для визначення порядку складності.
1,5 * N = O (N)
З другого правила випливає, що порядок складності добутку двох функцій дорівнює добутку їх складнощів.
O ((17 * N) * N) = O (17 * N) * O (N) = O (N) * O (N) = O (N * N) = O (N2)
З третього правила випливає, що порядок складності суми функцій визначається як порядок домінанти першого і другого доданків, тобто вибирається найбільший порядок.
O(N5 + N2) = O(N5)
Складність алгоритмів.
O (1)
Більшість операцій в програмі виконуються тільки раз або тільки кілька разів. Алгоритмами константної складності. Будь-який алгоритм, завжди вимагає незалежно від розміру даних одного і того ж часу, має константну складність.
О (N)
Час роботи програми лінійно зазвичай коли кожен елемент вхідних даних потрібно обробити лише лінійне число разів.
О (N2), О (N3), О (Nа)
Поліноміальна складність. О (N2)-квадратична складність, О (N3) - кубічна складність
О (Log (N))
Програма з логарифмічним часом роботи, починає працювати набагато повільніше зі збільшенням N. Такий час роботи зустрічається зазвичай у програмах, які ділять велику проблему в маленькі і вирішують їх окремо.
O (N * log (N))
Такий час роботи мають ті алгоритми, які ділять велику проблему в маленькі, а потім, вирішивши їх, з'єднують їх вирішення.
O (2N)
Експоненціальна складність. Такі алгоритми найчастіше виникають в результаті підходу іменованого як метод грубої сили.
Програміст повинен вміти проводити аналіз алгоритмів і визначати їх складність. Часова складність алгоритму може бути порахована з аналізу його керуючих структур.
Алгоритми без циклів і рекурсивних викликів мають константну складність. Якщо немає рекурсії і циклів, всі керуючі структури можуть бути зведені до структур константної складності. Отже, і весь алгоритм також характеризується константної складністю.
Визначення складності алгоритму в основному зводиться до аналізу циклів і рекурсивних викликів. Наприклад, розглянемо алгоритм обробки елементів масиву.
For i: = 1 to N do
Begin
...
End;
Складність цього алгоритму O (N), тому що тіло циклу виконується N раз, і складність тіла циклу дорівнює O (1).
Якщо один цикл вкладений в інший і обидва цикли залежать від розміру однієї і тієї ж змінної, то вся конструкція характеризується квадратичною складністю.
For i: = 1 to N do
For j: = 1 to N do
Begin
...
End;
Складність цієї програми О (N2).
Приклад.
Оцінимо алгоритм бінарного пошуку в масиві - дихотомію.
Суть алгоритму: йдемо до середини масиву і шукаємо відповідність ключа значенням серединного елемента. Якщо нам не вдається знайти відповідності, ми дивимося на відносний розмір ключа і значення серединного елемента і потім переміщаємося в нижню або верхню половину списку. У цій половині знову шукаємо середину і знову порівнюємо з ключем. Якщо не виходить, знову ділимо на половину поточний інтервал.
function search (low, high, key: integer): integer;
var mid, data: integer;
begin
while low <= high do
begin
mid: = (low + high) div 2;
data: = a [mid];
if key = data then
search: = mid
else
if key <data then
high: = mid-1
else
low: = mid +1;
end;
search: =- 1;
end;
Вирішення:
Перша ітерація циклу має справу з усім списком. Кожна наступна ітерація ділить навпіл розмір підсписку. Так, розмірами списку для алгоритму є n n/21 n/22 n/23 n/24... n/2m
Зрештою буде таке ціле m, що n/2m <2 або n <2m +1
Так як m - це перше ціле, для якого n/2m <2, то повинно бути правильно
(n/2m-1 > = 2) або (2m <= n)
З цього випливає, що 2m = < n <2m+1
Візьмемо логарифм кожної частини нерівності і отримаємо m =< (log2n = x) <m +1
Значення m - це найбільше ціле, яке = <х.
Отже, O (log2n).






