Рассмотрим основные характеристики, свойственные измерительным преобразователям. Эти характеристики позволяют ответить на вопрос о принципиальной возможности применения данного преобразователя в конкретном измерительном устройстве.
Функция преобразования устанавливает связь между входной и выходной величинами преобразователя у=f (х), где х- входная, а у - выходная величины. Функцию преобразования часто называют характеристикой измерительного преобразования. Зависимость у=f(х) может быть задана аналитически, графиком, таблицей. Преобразователь вида:
у=ах+b
где а и b - постоянные коэффициенты, называется линейным. В линейных преобразователях коэффициенты а и & не зависят от значения входной величины х. При этом коэффициент является коэффициентом передачи.
Примером простейшего линейного измерительного преобразователя является терморезистор, электрическое сопротивление которого R0 меняется в зависимости от температуры θ окружающей среды в соответствии с уравнением:
Rθ = R0 + αR0θ
Здесь R0 - сопротивление терморезистора при нулевой температуре θ=0; α - температурный коэффициент сопротивления. Считая входным параметром преобразователя температуру θ, коэффициенты преобразования можем определить следующим образом:
а =α R0; b = R0.
При преобразовании переменных во времени, например синусоидальных токов или напряжений, происходит изменение не только амплитуды величины, но и ее фазы. Поэтому коэффициент преобразования в общем виде представляет собой комплексную величину, зависящую от частоты сигнала.
Точность преобразователя определяет степень отличия действительной функции преобразования от номинальной, т.е. проектной. Точность оценивается погрешностью, под которой понимают разность между действительной и номинальной функциями преобразования. При этом погрешности приводят ко входу или выходу преобразователя.
Абсолютной погрешностью измерительного преобразователя по входу Δх называют разность между значениями выходной величины у,
приведенной ко входу, и входной величины х:
Δx = Y/Kн – Х
где Кн - номинальный коэффициент преобразования.
Абсолютной погрешностью преобразователя по выходу Δу называют разность между значениями входной величины, приведенной к выходу, и выходной величины:
Δy= ХКн – Y
Относительная погрешность измерительного преобразователя равна отношению абсолютной погрешности к значению входной или выходной величины, выраженному в процентах:
Δх Δу
δх ═ ——100; δy ═ —— 100.
X Y
Приведенная погрешность преобразователя представляет отношение абсолютной погрешности к нормирующему значению входной ХN идя выходной УN величины:
Δх Δу
γх ═ ——100; γy ═ —— 100.
XN YN
За нормирующее значение принимают полный диапазон возможных изменений входного (для ХN) или выходного (для YN) сигнала.
По источнику возникновения погрешности делятся на методические и инструментальные. Методические погрешности вызываются несовершенством метода преобразования, например, не учетом нелинейности элементов. Инструментальная погрешность возникает из-за несовершенства изготовления и наладки преобразования. По условиям возникновения различают основную и дополнительную погрешность. Основная погрешность проявляется в нормальных условиях эксплуатации. В нормальных условиях значения влияющих величин находятся в пределах, оговоренных стандартами или техническими условиями. Дополнительная погрешность возникает при отклонении условий эксплуатации от нормальных (но в пределах рабочих условий эксплуатации).
По характеру изменения погрешности преобразования могут быть систематические и случайные. Систематическая погрешность – это составляющая погрешности, остающаяся неизменной или меняющаяся закономерно. Случайная погрешность меняется случайным образом.
По зависимости от входного сигнала погрешности могут быть аддитивные и мультипликативные. Аддитивная погрешность не зависит от величины входного сигнала; она вызывается смещением нулевого уровня преобразователя. Мультипликативная погрешность пропорциональна величине входного сигнала; она вызывается нестабильностью функции преобразования. Суммарная абсолютная ΔΣ и относительная δΣ погрешности определяются суммой соответствующих аддитивных и
мультипликативных погрешностей:
ΔΣ ═ Δa+ Δ м; δΣ = δа+ δ м.
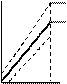
Примером измерительного преобразователя может служить усилитель постоянного тока с номинальным коэффициентом усиления К - рис.6.1. Напряжение смещения Uсм усилителя не зависит от К и является источником аддитивной погрешности, вызывая смещение характеристики преобразования усилителя. На рис. 6.2 показаны графики погрешностей для этого случая.
 Uсм
Uсм
K
Uвх Uвых
Рис. 6.1. Напряжение смещения в усилителе постоянного тока.

 y Δ а ΔM ΔΣ
y Δ а ΔM ΔΣ
0 x 0 x 0 x
 a) г) ж)
a) г) ж)
 Δа Δ М ΔΣ
Δа Δ М ΔΣ
 |
0 х 0 х 0 х
б) д) з)
 |
 δа δм δΣ
δа δм δΣ
0 х 0 х 0 х
в) е) и)
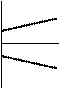
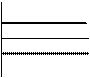
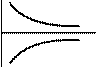
Рис. 6.2. Погрешности измерительных преобразований:
а, б, в – аддитивные; г, д, е – мультипликативные;
ж, з, и – суммарные.
 h(t)
h(t)
К Рис. 6.3. Переходная функция пропорционального
элемента.
0 t
Чувствительность измерительного преобразователя – это отношение изменения выходного сигнала к вызвавшему его изменению входного сигнала. Отношение S=ΔY/ΔX есть средняя чувствительность преобразователя на интервале ΔХ, а предел, к которому стремится это отношение при ΔХ→ 0, есть чувствительность преобразователя в точке Х:
DY
S ═ lim Scp ═ ——.
ΔX→0 dX
Если Y и Х величины однородные, то чувствительность величина безразмерная. Различают абсолютную и относительную чувствительности преобразователя. Абсолютная чувствительность – это S=dY/dX, а относительная – S0=(dY/Y)/(dX/X). Например, чувствительность тензо-метрического преобразователя определяется как отношение относительного изменения электрического сопротивления ΔR/R к относительной деформации Δl/l.
Если функция преобразования линейна, то S - соnst и не зависит от Х. Например, если у=ах+ b, то S=а.
Если функция преобразования нелинейна, то S≠Scp и зависит от Х. Например, если у=ах2+b, то а=2ах.
Порог реагирования – это минимальное изменение входной величины, вызывающее уверенно различимое приращение выходной величины преобразователя на фоне шумов, смещения нуля, гистерезиса характеристики и прочих мешающих факторов.
Входное и выходное сопротивления определяют степень согласования преобразователя с источником сигнала и с нагрузкой. Так, если преобразуемый сигнал напряжение, то Zвх должно быть максимальным, а если ток – то минимальным. В общем виде входное сопротивление должно быть таким, чтобы минимизировать мощность, потребляемую от источника сигнала.
Быстродействие характеризует способность быстро реагировать на
изменение входного сигнала. В общем виде динамические свойства преобразователя характеризуются дифференциальным уравнением, связывающим выходную и входную величины. Решение этого уравнения при известном х(t) дает значение у(t). Порядок уравнения и его коэффициенты определяются структурой и параметрами преобразователи. На практике такую методику в прямом виде практически не используют в связи со сложностью решения дифференциальных уравнений высоких порядков.
Чаще для описания динамических свойств преобразователей используют характеристические функции, которые можно получить экспериментально, подавая на вход специальный тестовый сигнал, например, скачкообразный или гармонический. Реакция преобразователи на скачкообразное входное воздействие единичной амплитуды называется переходной функцией преобразователя h(t). Очень часто сложный преобразователь при анализе динамических процессов разбивают на простейшие динамические звенья. Переходные функции основных
динамических элементов (пропорционального, апериодического, колебательного, интегрирующего, дифференцирующего и запаздывания) приведены на рис. 6.3 - 6.8.
 h(t)
h(t)
K Рис 6.4. Переходная функция апериоди-
ческого элемента.
0 t
T
h(t)

K Рис. 6.5. Переходная функция колебатель-
ного элемента.
0 t
h(t)
 Рис. 6.6. Переходная функция интегриру-
Рис. 6.6. Переходная функция интегриру-
ющего элемента.
0 t
h(t)

Рис. 6.7. Переходная функция дифферен-
S=K цирующего элемента.
 0
0
T→ C
H(t)
 Рис. 6.8. Переходная функция элемента
Рис. 6.8. Переходная функция элемента
K запаздывания.
0 τ t
Если тестовый сигнал имеет гармонический характер х=Хm sin ωt, то в линейных преобразователях выходной сигнал тоже будет гармоническим, но с другой амплитудой и фазой:
у = Ymsin(ωt+φ)
Зависимость Ym от частоты ω при постоянном Хm называется амплитудно-частотной характеристикой преобразователя, а зависимость φ от ω - фазочастотной. В общем виде передаточные свойства преобразователей характеризуются не коэффициентом, а функцией преобразования, которая является комплексной величиной и зависит от ω. В теории регулирования
принято передаточные функции указывать не в функции времени, а в функции специального частотного аргумента Р. Такую передаточную функцию W(р) получают путем применения преобразования Лапласа к преобразовательной функции времени Y(t)/Х(t). Преобразование Лапласа над переменной Z(t) представляет собой операцию:
∞
Z(p)=∫ Z(t) e-pt dt
Переход от функции времени t к новому аргументу Р позволяет заменить дифференциальное уравнение динамики алгебраическим. Дифференцирование эквивалентно умножению на аргумент Р, а интегрирование - делению на Р.
Приведем значения передаточных функций W(р)=Y(р)/Х(р) для простых динамических элементов.
1. Пропорциональный (усилительный элемент):
W(p)=K,
где К - коэффициент преобразования, К=соnst, рис. 6.3.
2. Апериодический элемент:
К
W(p) ═ ———
Tp+1
где Т - постоянная времени элемента, определяющая его инерционность - рис. 6.4.
3. Колебательный элемент:
К
W(p) ═ ———————
T2p2+2Tεp+1
Здесь ε декремент затухания колебаний – рис. 6.5.
4. Интегрирующий элемент:
К
W(p) ═ ——
Р
5. Дифференцирующий элемент:
W(p) = KP.
Переходная функция такого элемента представляет собой импульс бесконечно малой длительности, площадью, равной коэффициенту передачи- рис. 6.7.
6. Запаздывающий элемент:
W(p) = Ke-pτ
где τ - время запаздывания, рис.6.8.
Сложный преобразователь представляет собой соединение простейших динамических элементов. По передаточным функциям элементов, зная характер соединения их между собой, можно определить передаточную функцию всего преобразователя. При этом следует использовать следующие правила (рис. 6.9):
1. Последовательное соединение элементов:
W(p) = W1(p)W2(p).
2. Параллельно-согласное соединение элементов:
W(p) = W1(p) + W2(p).
З. Параллельно-встречное соединение элементов (соединение с обратной связью):
W1(p)
W(p) ═ ———————
1 ± W1(p)W2(p)
Знак «+» относятся к отрицательной обратной связи, а знак «–» - к положительной обратной связи.
Зная передаточную функцию преобразователя, можно аналитически вычислить характер переходного процесса, определить степень устойчивости преобразователя как элемента автоматического регулирования, вычислить статическую или динамическую ошибки преобразования.










 x W1(p) W2(p) y W1(p) x W1(p) y
x W1(p) W2(p) y W1(p) x W1(p) y

 x y
x y


 а) W2(p) W2(p)
а) W2(p) W2(p)
б) в)
Рис. 6.9. Соединение элементов преобразования:
а – последовательное; б – параллельное согласное;
в – параллельное встречное.






