СГТУ
Кафедра прикладной физики.
Лабораторная работа №1.
Физический маятник.
Теоретический отчет:
Выполненная работа:
Окончательный отчет:
Выполнила: Газенкампф Е.Н. ИСТ-11.
Цель работы:
Изучение гармонических колебаний; определение приведенной длины физического маятника и ускорения свободного падения.
Теоретические сведения.
Гармонические колебания - это такие колебания, когда смещение тела от положения равновесия зависит от времени по закону синуса или косинуса:
X=Asin(wt+j °) или X=Acos(wt+j°), (1)
где X-величина смещения тела от положения равновесия, А - амплитуда колебания – максимальное смещение от положения равновесия; wt+j° - фаза колебания, определяющая положение колеблющегося тела в данный момент.
Частота колебаний (g) равна числу полных колебаний, совершаемых за единицу времени. Единица частоты колебаний Герц (Гц). Периодом колебаний (Т) называется промежуток времени, за который совершается одно полное колебание. Тg=1.
Циклическая частота колебания численно равна числу полных колебаний, совершаемых за 2p секунд: w=2pg.
Тело совершает гармонические колебания, когда на него действует упругая сила, пропорциональная величине смещения от положения равновесия: F=-kX, (2)
где k – коэффициент упругости. Знак минус указывает, что возвращающая сила направлена в сторону, противоположную смещению, то есть к положению равновесия.
Второй закон Ньютона для колеблющегося тела: ma=F или
md²x/dt²=-kX (3)
d²x/dt²+kX/m=0 k/m=j ² (4)
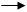d²x/dt²+j °²X=0. (5)
Это и есть дифференциальное уравнение гармонических колебаний. Одним из решений такого уравнения является X=Acos(wt+j°). Циклическая частота колебаний j° называется циклической частотой собственных колебаний. Период таких колебаний:
T=2π √m/k. (6)
Кинетическая энергия колеблющейся точки массой m:
Eкин=mv²/2 =(mj °² A²cos²j ° t)/2.
Потенциальная энергия квазиупругих сил, отсчитываемая от положения равновесия данной материальной точки:
Епот=kx/2=(kAsin t)/2=(mj °²A² sin²j °t)/2, где X – смещение колеблющейся точки от положения равновесия, k – коэффициент квазиупругой силы.
Полная энергия материальной точки, совершающей гармоническое колебание с частотой w и амплитудой A: E=Eкин+Eпот.
В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но полная энергия – величина постоянная, она пропорциональна квадрату амплитуды колебаний.
Собственные гармонические колебания системы – это идеальный случай колебаний, когда энергия системой не теряется и амплитуда остается постоянной. В случае реальных колебаний энергия, переданная системе, постепенно расходуется на преодоление сил сопротивления, поэтому амплитуда колебаний уменьшается, колебания затухают. Эти колебания называют затухающими (рис. 1б,в). Их частота определяется свойствами колеблющейся системы – массой, возвращающей силой, сопротивлением.
Рис.1
а б в
β=0, То=2p\wо wо>β, T=2p\√ wо²- β² wо<β, T=∞
Если сила сопротивления среды пропорциональна скорости колебания, то есть Fсопр=-rdx\dt, второй закон Ньютона для колеблющейся точки запишется:
md²x\dt² =Fупр+Fсопр или md²x\dt²+rdx\dt+kx=0. (7)
Введем обозначения 2β =r\m; wо² =k\m.
Решение уравнения (7) имеет вид:
X=Xоe cos(wt+jо) (8)
Амплитуда затухающих колебаний уменьшается по закону Xоe (рис.1б), частота затухающих колебаний w=√ wо²- β² < wо (9)
Если wо<β, частота является мнимым числом и имеет место апериодический процесс – рис.1в.
В случае затухающих колебаний энергия убывает по закону
E(t)=Eоe (10)
Величина отношения энергии к мощности потерь за время T\2p=1\w характеризует способность колебательной системы сохранять энергию и называется добротностью Q =E(t)w\2βE(t)=w\2β=p\Tβ (11)
Добротность равна числу колебаний за время, за которое амплитуда уменьшается в e раз, а энергия в e раз. Степень затухания колебаний характеризуется логарифмическим декрементом, который определяет затухание колебаний за период:
O=ln(x(t)\x(t+T))= βT (12)
Каждое тело, подвешенное в точке, лежащей выше его центра тяжести, может колебаться и представлять собой физический маятник. На рис. 2 изображен физический маятник, отклоненный от положения равновесия.
Через точку О перпендикулярно рисунку проходит неподвижная ось, вокруг которой совершаются колебания, С – центр тяжести маятника (точка, в которой приложена сила тяжести mg).
Момент силы mg относительно оси О равен M=-mglcsinα, где lc – расстояние от оси вращения до центра тяжести точки С. При малых углах отклонения, когда можно принять sinα=α, основной закон динамики вращательного движения, описывающий колебания такого маятника, можно записать в виде:
Jd²α\dt²=-mglcα или d²α\dt²+mglcα\J=0, (13)
Где J – момент инерции физического маятника относительно оси вращения. Это уравнение аналогично дифференциальному уравнению (5); величина mglc\J является квадратом круговой частоты гармонических колебаний:
mglc\J= wо² (14)
Решение уравнения (13) α=αоcos(wоt+j°) описывает гармонические колебания, совершаемые физическим маятником. Период таких колебаний:
T=2π √J\ mglc (15)
Для математического маятника (математическим маятником называют колеблющееся тело, размерами которого можно пренебречь по сравнению с расстоянием от центра масс тела до оси вращения) в случае малых углов отклонения дифференциальное уравнение колебаний выглядит:
d²α\dt²=-g α \l (16)
Период колебания математического маятника:
T=2π √l\ g (17)
Физический маятник,, описываемый (13), колеблется с таким же периодом, как и математический маятник, описываемый (16), имеющий длину lо=J\mlc, где lc - расстояние от О до С.
Приведенной длинной lофизического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.
Если к оси физического маятника подвесить грузик на нити такой длины, чтобы она была равна приведенной длине данного физического маятника (рис. 3), то отклоненные на одинаковый угол физический маятник и грузик колеблются вместе, так что грузик все время находится в одной и той же точке физического маятника – его центре качаний. Приведенная длина lо всегда больше lc, то
есть центр качаний всегда лежит ниже центра тяжести. По теореме Штейнера момент инерции относительно оси маятника J=Jо +m lc², где Jо – момент инерции относительно оси, проходящей через центр тяжести. Поэтому приведенная длина будет lо=(Jо+mlc²)\ mlc = lc+ Jо \mlc,т.е. больше lc.
Точка подвеса и центр качаний обратимы. Теорема Гюйгенса: если физический маятник подвесить за центр качания, его период не изменится и прежняя точка подвеса будет новым центром качания.
Оборотный маятник (рис. 4) состоит из стального стержня, на котором закрепляются опоры 1 и 2 в виде призм и грузы 3 и 4.
Метод оборотного маятника основан на сопряженности двух его точек: точки подвеса и центра качаний. Путем изменения расстояний между опорами или между грузами добиваются такого расположения грузов на стержне, чтобы период колебаний маятника при его переворачивании не изменился. При выполнении этого условия расстояние между опорами будет являться приведенной длинной маятника l о =L+X.
Теоретически рассчитать положение центра масс физического маятника можно для упрощенной модели маятника (рис. 5), состоящей из невесомого стержня с закрепленными на нем материальными точками 3 и 4. Если расстояние от груза 4 до опоры 1 обозначить L, то расстояние от центра масс (точка С) до опор выразится: lcl=(x+L)\2, lc2=l о -(x+L)\2=(2l о -x-L)\2 (21)
Моменты инерции физического маятника относительно осей, проходящих через точки 1 и 2 могут быть рассчитаны по формулам:
J1=l оml cl, J2=l оml c2 (22)
