Для розгляду можливих варіантів напрямку ПВ з одним транзитом
складається допоміжна табл. 4. В основу складання таблиці беруться
обмеження за навантаженням для транзитних вузлів.
Таблиця 4
| Пункти відправлення | Пункти призначення | ||||||||
| 2,8 | |||||||||
| 9,1 | |||||||||
| 7,4 | 9,7 | ||||||||
| 7,5 | |||||||||
| 7,4 | |||||||||
| 7,5 | |||||||||
| 8,3 | |||||||||
| 9,1 | 9,7 | ||||||||
| 2,8 | 8,3 |
У клітці 19 записані пункти призначення 2,8, що показує можливість
напрямку ПВ із вузла 1 у вузол 9 через вузли 2 або 8 з одним транзитом. Потік
ПВ, що направляється з пункту відправлення i в пункт призначення j через транзитний вузол k можна записати Xikj. Така форма запису невідомих полегшує перехід до моделі транспортної задачі. Користуючись табл. 4, побудуємо математичну модель, в яку включимо всі потоки з одним транзитом. Попередньо необхідно ввести нову індексацію невідомих і потоків. Перелік старих і нових індексів зведено в табл. 5. Номер чергового індексу визначається черговою заповненою кліткою табл. 4 при перегляді рядків у напрямку зліва направо й вниз. Наприклад, навантаження з вузла 1 у вузол 9 позначається по старому Q19, а по новому Q1. Навантаження з 2 у 8 по старому позначається Q28, а по новому Q2 і т.д. Потік ПВ з 1 у 9 через вузол 2 по старому позначався X219, а по новому буде X21, тобто номер транзитного вузла 2 стає першою цифрою індексу, а 19 замінюється 1, тому що Q19 було замінено на Q1 і записується другою цифрою індексу X21. Потрібно читати X21 - потік із пункту відправлення 2 у пункт призначення 1.
Таблиця 5
| Стара індексація | Нова індексація | Стара індексація | Нова індексація | Стара індексація | Нова індексація |
| Q19 | Q1 | X219 | X21 | X764 | X77 |
| Q28 | Q2 | X819 | X81 | X564 | X57 |
| Q35 | Q3 | X219 | X92 | X879 | X88 |
| Q38 | Q4 | X928 | X12 | X379 | X38 |
| Q46 | Q5 | X128 | X73 | X982 | X99 |
| Q53 | Q6 | X735 | X43 | X182 | X19 |
| Q64 | Q7 | X435 | X94 | X983 | X9,10 |
| Q79 | Q8 | X938 | X74 | X783 | X7,10 |
| Q82 | Q9 | X738 | X75 | X291 | X2,11 |
| Q83 | Q10 | X746 | X55 | X891 | X8,11 |
| Q91 | Q11 | X753 | X76 | X897 | X8,12 |
| Q97 | Q12 | X453 | X46 | X397 | X3,12 |
Далі з урахуванням нової індексації складається транспортна табл. 6. За цією таблицею під транспортними вузлами потрібно розуміти склади 1, 2, 3, 4, 5, 6, 7, 8, 9, тобто пункти відправлення з розміром запасів W11, W12, W13, W14, W15, W16, W17, W18, W19, а під потоками - пункти споживання однорідного вантажу 1,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 із потребами Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8, Q9, Q10, Q11, Q12. На відміну від транспортної задачі в її звичайній постановці, тут перевезення однорідного вантажу з певного вузла допускається тільки в певний пункт споживання. Тому за тими напрямками, де перевезення не допускається, витрати на перевезення одиниці вантажу приймаються рівними M. Під M розуміється велике значення розміру витрат, що фактично виключає з розгляду цю змінну. Перевезення ПВ у заданих кількостях може бути реалізовано тільки в тому випадку, якщо сумарна пропускна спроможність вузлів буде не менше сумарного розміру потоків, тобто:

Розглянута задача відповідає відкритій моделі транспортної задачі. Потреба введення фіктивного пункту споживання визначається як різниця:

| Пункти відправлення | Пункти призначення | |||||||||||||
| ф | 
| |||||||||||||
| М | С1 | М | М | М | М | М | М | С1 | М | М | М | О | 
| |
| С2 | М | М | М | М | М | М | М | М | М | С2 | М | О | 
| |
| М | М | М | М | М | М | М | С3 | М | М | М | С3 | О | 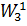
| |
| М | М | С4 | М | М | С4 | М | М | М | М | М | М | О | 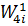
| |
| М | М | М | М | С5 | М | С5 | М | М | М | М | М | О | 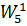
| |
| М | М | С7 | С7 | С7 | С7 | С7 | М | М | С7 | М | М | О | 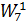
| |
| С8 | М | М | М | М | М | М | С8 | М | М | С8 | С8 | О | 
| |
| М | С9 | М | С9 | М | М | М | М | С9 | С9 | М | М | О | 
| |

| 
| 
| 
| 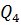
| 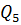
| 
| 
| 
| 
| 
| 
| 
| 
|
Транспортна таблиця являє собою матрицю 9 на 13, в якій є 24 невідомих, що представляють собою обсяги перевезених ПВ з пунктів відправлення в пункти призначення. Ці невідомі Xij повинні бути записані в тих клітинах таблиці, в яких проставлені значення витрат у транзитних вузлах Cі. Рішення задачі можна спростити, якщо поділити загальне число невідомих на дві групи (підзадачі), в яких змінні будуть незалежними, тобто будуть знаходитися в різних рядках і стовпцях табл. 6. Так, наприклад, змінні X12, X19, X55, X57, X43, X72, X74, X75, X76, X77, X7,10, X92, X94, X99, X9,10 можна віднести до першої групи, а змінні X21, X2,11, X38, X3,12, X81, X88, X8,11, X8,12 - до другої. У цьому випадку одержимо начебто дві самостійні підзадачі. Перша з них включає 5 пунктів відправлення 1, 5, 4, 7, 9 і 8 пунктів призначення 2, 3, 4, 5, 6, 7, 9, 10, а друга - 3 пункти відправлення 2, 3, 8 і 4 пункти призначення 1, 8, 11, 12. Незаповнені матриці цих двох спрощених підзадач наведені в табл. 7 і 8.
Таблиця 7
| Пункти відправлення | Пункти призначення | ||||||||||
| ф | 
| ||||||||||
| С1 | М | М | М | М | М | С1 | М | О | 
| ||
| М | С4 | М | М | С4 | М | М | М | О | 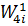
| ||
| М | М | М | С5 | М | С5 | М | М | О | 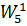
| ||
| М | С7 | С7 | С7 | С7 | С7 | М | С7 | О | 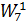
| ||
| С9 | М | С9 | М | М | М | С9 | С9 | О | 
| ||

| 
| 
| 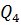
| 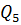
| 
| 
| 
| 
| 
|
Таблиця 8
| Пункти відправлення | Пункти призначення | |||||
| ф | 
| |||||
| С2 | М | С2 | М | О | 
| |
| М | С3 | М | С3 | О | 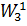
| |
| С8 | С8 | С8 | С8 | О | 
| |

| 
| 
| 
| 
| 
|






