Системы шифрования с открытым ключом

 

В таких системах используется два ключа: информацию шифруется с помощью открытого ключа, а расшифровывается с помощью секретного ключа. В основе применения систем с открытым ключом лежит использование необратимых или односторонних функций. Эти функции обладают следующим свойством:

при известном х легко определяется у

y = f(x)

но по известному значению у практически невозможно получить х. В криптографии используются односторонние функции, имеющие так называемый потайной ход. Эти функции с параметром Z обладают следующими свойствами: для определённого Z могут быть определены алгоритмы E_z и D_z. С помощью E_z легко получить функцию f_z(x) для всех х из области определения. Также просто с помощью D_z получается обратная функция:

x = f_z’(y)

для всех у из области допустимых значений. При этом практически для всех Z и практически для всех у из области допустимых значений нахождение f’(y) невозможно только при известном E_z. Таким образом, в качестве открытого ключа используется у, а в качестве закрытого – х.

При шифровании с использование открытого ключа нет необходимости в передаче секретного ключа между взаимодействующими субъектами, что существенно упрощает криптозащиту передаваемой информации.

Криптосистемы с открытыми ключами различаются видами односторонних функций. Среди них известными являются RSA(Rivers Shamir Aldemn) Эль-Гамаля, Мак-Элиса. Наиболее эффективным и распространённым алгоритмом шифрования с открытым ключом является алгоритм RSA. Алгоритм основан на использовании операции возведения в степень модульной арифметики. Его можно представить в виде следующей последовательности шагов:

1) Выбираются два больших простых числа p и q

2) Получается или вычисляется открытая компонента ключа

3) Вычисляется функция Эйлера . Функция Эйлера показывает количество целых положительных чисел от 1 до n, которые взаимно просты с n.

4) Выбирается большое простое число d, которое является взаимно простым с функцией Эйлера.

5) Определяется число e, которое удовлетворяет условию.

Алгоритм основан на использовании операции возведения в степень модульной арифметики. Его можно представить в виде следующей последовательности шагов:

Данное условие означает что остаток от деления или вычет произведения e*d на функцию Эйлера равен 1. Число е принимается в качестве компоненты открытого ключа. В качестве секретного ключа используются числа d и n.

6) Исходная информация, независимо от ее физической природы представляется в двоичном виде. Последовательность бит разделяется на блоки длинной L бит, где L – наименьшее целое число удовлетворяющее условию:

Каждый блок рассматривается как целое положительное число X(i), принадлежащее интервалу от (0; -1). Таким образом исходная информация представляется последовательностью чисел X(i), i=(1;I) I определяется длиной шифруемой последовательности.

7) Зашифрованная информация получается в виде последовательности чисел Y(i), вычисляемых по формуле:

8) Для расшифрования информации используется следующая зависимость:

Пусть необходимо зашифровать сообщение ГАЗ

Г – 4; А – 1; З – 9; (номер буквы в алфавите)

000100 000001 001001

1) Выбираем p=3 и q=11

2) n=p*q=33

3) f(p,q)=20

4) d=3 (выбирается от 1 до n произвольно)

5) (e*3)mod20=1

e=7.

Чем меньше е тем более уязвимый алгоритм.

6) L=6; 6 разрядов обеспечат коды для всех букв русского алфавита.

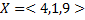- исходный кортеж.

7) {7,33}

Y=<16,1,15>

8)

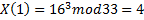
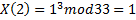
X=<4,1,9>

 

Система Эль-Гемаля основана на сложности вычисления дискретных логарифмов в конечных полях. Основным недостатком данной системы является необходимость выполнения трудоемких операций в модульной арифметике, что требует привлечения значительных вычислительных ресурсов. Криптосистема Мак-Эллиса использует коды исправляющие ошибки. Она реализуется в несколько раз быстрее чем криптосистема RSA, но имеет существенный недостаток: в криптосистеме Мак-Эллиса используется ключ большой длинны и получаемый шифротекст в два раза превышает исходный текст. Для всех методов шифрования с открытым ключом математически строго не доказано отсутствие других методов криптоанализа, кроме решения задачи полного перебора. (NP полная задача). Если появятся методы эффективного решения таких задач, то криптосистемы такого типа будут дискредитированы. Криптостойкость рассмотренных методов шифрования определяется длинной ключа. Для современных систем длина ключа должна быть не менее 100 бит. Для ответственных применений секретным является не только ключ, но и алгоритм шифрования. Для повышения криптостойкости шифров могут использоваться несколько ключей. Зашифрованная с помощью первого ключа информация затем подвергается зашифровке вторым ключом и так далее. Предлагают использовать переменные алгоритмы шифрования. В этом случае ключ шифрования используется еще и для выбора конкретного алгоритма шифрования. Криптостойкость такого способа или метода шифрования пока еще сложно строго доказуемо. Привлекательность методов шифрования с использованием открытых ключей заключается прежде всего в отсутствии рассылки секретных ключей. Перспективным направлением развития криптозащиты информации является стеганография, комплексное использование стеганографии и шифрования намного повышает криптостойкость закрытой информации.