Нейрон и его искусственная модель.
Нейроном называют нервную клетку, т.е. базовый элемент нервной системы (человека или другого живого существа). В частности, считается, что мозг человека состоит из примерно 
нейронов, которые имеют между собой примерно 
соединений.
В каждом нейроне выделяют тело нервной клетки, называемое сомой, и два вида отростков:
▪ дендриты (по которым в нейрон поступает входная информация);
▪ аксон (по которому нейрон передает свою выходную информацию).
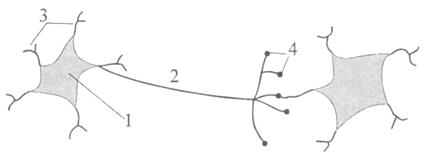
Рис. 1. Упрощенная модель нейрона и его связи с другим нейроном:
1 – тело клетки (сома), 2 – аксон, 3 – дендриты, 4 – синапсы.
Каждый нейрон взаимосвязан с определенным множеством других нейронов и передает возбуждение на них через нервные стыки, называемые синапсами.
Синапсы играют роль неких преобразователей передаваемой от нейрона информации. Они могут усиливать или, наоборот, ослаблять возбуждение связываемых с данным нейроном других нейронов. В итоге к какому-либо конкретному нейрону часть сигналов от других нейронов может его возбуждать, а от других оказывать тормозящее воздействие.
Модель искусственного нейрона вида (1.2) представлена на рис. 2.
В качестве функции 
ныне используют на практике не только функция (1.2), предложенная МакКалахом (Mc Culloch W.S.) и Питтсом, но ряд других. Например, применяют
(1.4)
или
(1.5)
Но наиболее часто в настоящее время используют для модели искусственного нейрона в качестве сигмоидальную функцию, определяемую выражением
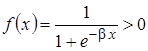. (1.6)
Если в (1.6) 
, то характеристика будет приближаться к пороговой униполярной функции (1.3).
В моделях искусственного нейрона используется также в качестве альтернативы рассмотренным выше функциям функция гиперболического тангенса
. (1.7)
Простейший персептрон и его характеристика.
Модель МакКаллоха–Питтса послужила Розенблатту основой для построения в конце 1950-х – в начале 1960-х годов простейшей однонаправленной нейронной сети, которую он назвал персептроном. В настоящее время этот персептрон часто называют простейшим персептроном (рис. 5). В качестве функции в нем применялась биполярная функция активации (1.4), график которой приведен на рисунке 3, б.
В этом персептроне сигнал на выходе линейной части определяется выражнением
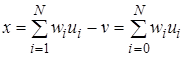, (1.8)
где 
.
Задачей такого персептрона является классификация вектора входных для него переменных 
, смысл которой заключается в отнесении их к одному из двух классов, обозначаемых как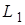 
и 
. Персептрон должен отнести вектор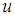 
к классу 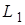, если выходной сигнал нелинейной части персептрона 
принимает значение 1, или к классу , если сигнал принимает значение –1. Таким образом, персептрон разделяет 
-мерное пространство входных векторов 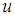на два подпространства. Это разделение осуществляется 
-мерной гиперплоскостью, определяемой уравнением
. (1.9)
Гиперплоскость (1.9) обычно называют решающей границей (decision boundary). Если 
, то решающая граница на плоскости входных векторов 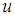представляет собой прямую линию (рис. 6), задаваемую уравнением
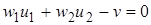. (1.10)
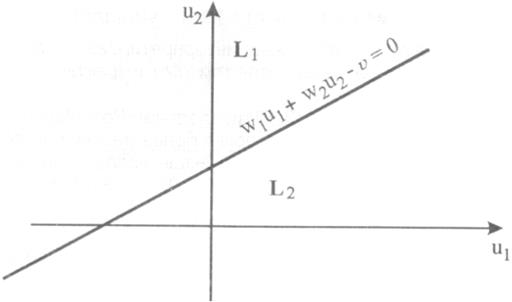
Рис. 6. Решающая граница для простейшего персептрона при
Точки в этой плоскости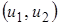 
, лежащие над этой прямой, относятся к классу 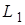, а лежащие под этой прямой – к классу . Точки, лежащие на решающей границе относятся в классу 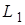(вследствие принятой бинарной характеристики нелинейности согласно (1.4)).
Полагаем, что в исходном состоянии персептрона веса 
в уравнении гиперплоскости (1.9) неизвестны. Они должны быть определены в процессе обучения персептрона. Для этого на вход персептрона последовательно подаются так называемые обучающие сигналы 
, где 
. Такой способ обучения (в данном случае персептрона) называется «обучением с учителем» или «обучение под надзором». Роль учителя фактически сводится к корректному отнесению сигналов к классам 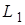или , несмотря на неизвестность весов уравнения решающей границы (1.9).
После завершения процесса обучения персептрон должен самостоятельно корректно классифицировать поступающие на его вход сигналы 
в том числе и те, которые отсутствовали в обучающей последовательности.
При решении поставленной задачи будем полагать, что входные последовательности действительно удовлетворяют условию классификации, т.е. могут быть разделены на два класса 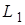или , разграниченные между собой гиперплоскостью (1.9).
В 
-й момент времени сигнал на выходе линейной части персептрона определяется выражением
, (1.11)
где
; (1.12)
. (1.13)
Обучение персептрона заключается в рекуррентной коррекции вектора весов 
так, что
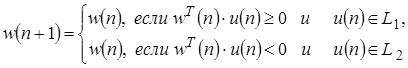(1.14)
и
(1.15)
В приведенном алгоритме обучения 
- шаг коррекции, а начальное значение вектора весов 
.
Алгоритм (1.14) и (1.15) можно записать в более сжатом виде. Для этого определим так называемый эталонный (заданный) сигнал 
как
(1.16)
Выходной сигнал персептрона можно представить в виде:
. (1.17)
В итоге алгоритм обучения (1.14) и (1.15) можно записать в виде:
. (1.18)
Здесь 
– величина, которую можно рассматривать как погрешность между эталонным (заданным) сигналом и текущим выходным сигналом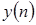 
.
Сходимость алгоритма (1.18) была доказана самим Розенблаттом и рядом других исследователей. Доказано, что для принятой выше линейной сепарабельности входных сигналов согласно (1.9) алгоритм (1.19) сходится, т.е., начиная с некоторого шага 
, получаем
.
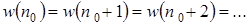После завершения обучения решающая граница персептрона будет определяться уравнением
и персептрон будет корректно классифицировать не только сигналы обучающей выборки 
, но и другие входные сигналы 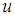, удовлетворяющие условию линейной сепарабельности (1.9).
