Розрахунком складального розмірного ланцюга і наступним його моделюванням визначити можливість і умови досягнення потрібної точності замикаючої ланки методом повної і неповної взаємозамінності.
Вихідні дані: варіант – 1.1.1;
тип виробництва – одиничне, дрібносерійне;
замикаюча ланка –  ;
;
ступінь ризику – Р = 0,01%.
Експериментальна частина
6.5.1 Схема складального розмірного ланцюга
6.5.3 Моделюючи процес складання, складаємо 20 моделей вузла без будь-якого підбору деталей та вимірюємо значення АΔ для кожної з моделей. Результати вимірів заносимо до таблиці 6.1.
Таблиця 6.1 – Результати моделювання складання
| № П/П | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| АΔ, мм | 0,43 | 0,45 | 0,42 | 0,40 | 0,51 | 0,42 | 0,57 | 0,53 | 0,60 | 0,48 |
| № П/П | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| АΔ, мм | 0,51 | 0,54 | 0,41 | 0,37 | 0,67 | 0,38 | 0,45 | 0,44 | 0,37 | 0,51 |
6.5.4 Визначимо поле розсіювання та координату середини поля розсіювання замикаючої ланки складального розмірного ланцюга


6.5.5 Перевіримо можливість досягнення потрібної точності замикаючої ланки методом повної взаємозамінності, для чого складемо схему і розв’яжемо розмірний ланцюг методом максимуму-мінімуму.
- Визначаємо номінальний розмір замикаючої ланки за формулою

- Перевіряємо умову замикання ланцюга за номіналами:

Умова виконується.
- Визначаємо розрахункове значення величини допуску замикаючої ланки:

- Визначаємо середину поля допуску замикаючої ланки:
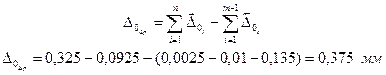
- Визначимо верхнє і нижнє граничні відхилення замикаючої ланки

- Виходячи з індивідуального завдання, визначаємо допуск і координату середини поля допуску замикаючої ланки:
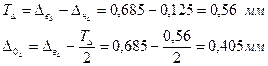
- Перевіримо теоретичну можливість складання за методом повної взаємозамінності

Так як ланцюг за допусками замикається, то і складання методом повної взаємозамінності можливе.
- Перевіримо практичну можливість складання методом повної взаємозамінності

Отже складання методом повної взаємозамінності можливе.
6.5.6 Перевіримо можливість досягнення необхідної точності замикаючої ланки методом неповної взаємозамінності, для чого розв’яжемо розмірний ланцюг імовірнісним методом.
- Визначаємо розрахункове значення величини допуску замикаючої ланки і координату середини поля допуску:


- Визначимо верхнє і нижнє граничні відхилення замикаючої ланки

- Порівнюємо розраховані та задані значення допуску і координати середини поля допуску замикаючої ланки:

Виконуються обидві умови замикання ланцюга за допусками. Отже, складання методом неповної взаємозамінності можливе.
6.5.7 Порівнюємо результати вимірів з допустимими граничними значеннями замикаючої ланки за технічними вимогами. Так як всі одержані розміри замикаючої ланки знаходяться в межах допуску, то відсоток браку складає 0, що менше заданого ступеню ризику (Р=0,01%), а отже складання за методом неповної взаємозамінності можливе.
Результати розрахунків зводимо до таблиці 6.2
Таблиця 6.2 – Результати роботи
| Розмірні параметри | Метод повної взаємозамінності | Метод неповної взаємозамінності | |
| Задані | АD , DвD, DнD | 
| 
|
| ТD | 0,56 | 0,56 | |
| D0D | +0,405 | +0,405 | |
| Виміряні | АDф , DвDф, DнDф | 
| 
|
| wDф | 0,49 | 0,30 | |
| D0Dф | +0,385 | +0,52 | |
| Розраховані | АDР , DвDР, DнDР | 
| 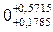
|
| ТDР | 0,5 | 0,393 | |
| D0DР | +0,375 | +0,375 | |
| Перевірка | ТDР ≤ ТD? | ТDР ≤ ТD | ТDР ≤ ТD |
| D0DР = D0D? | D0DР ¹ D0D | D0DР ¹ D0D | |
| Підтвердження | wDф ≤ ТD? | wDф ≤ ТD | wDф ≤ ТD |
| D0Dф = D0D? | D0Dф ¹ D0D | D0Dф ¹ D0D | |
| Складання можливе? | можливе | можливе |
Висновок
Опанували методику аналізу точності при складанні за методами повної і неповної взаємозамінності.
1) Експериментально встановили, що при даній точності складових деталей і зазору (замикаючої ланки) при одиничному та дрібносерійному типі виробництва зі ступенем ризику 0,01% можливе складання як за методом повної так і неповної взаємозамінності. Використання обох методів можливе так, як розрахункові величини полів допусків замикаючої ланки Т D Р як при методі повної так і при методі неповної взаємозамінності менше заданого поля допуску замикаючої ланки, причому розрахункові верхні граничні відхилення замикаючої ланки D в D Р менше заданого верхнього граничного відхилення D в D, а нижні розрахункові граничні відхилення D н D Р більше допустимого граничного нижнього відхилення D н D замикаючої ланки. Можливість використання обох методів складання також підтвердилось експериментально.






