В биномиальной системе счисления (англ.) число x представляется в виде суммы биномиальных коэффициентов:
где 
.
При всяком фиксированном значении 
каждое натуральное число представляется уникальным образом.
Система остаточных классов (СОК).
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором попарно взаимно простых модулей 
с произведением 
так, что каждому целому числу x из отрезка 
ставится в соответствие набор вычетов 
, где
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка .
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в .
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям 
.
Система счисления Штерна-Броко.
Система счисления Штерна-Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.
Перевод из одной системы счисления в другую
Перевод в десятичную систему счисления.
Если число в -ричной системе счисления равно
то для перевода в десятичную систему вычисляем такую сумму:
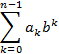
или, в более наглядном виде:
Например:
1011002 =
= 1 · 25 + 0 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 0 · 20 =
= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 =
= 32 + 8 + 4 + 0 = 4410
Перевод из десятичной системы счисления.
Целая часть:
-Последовательно делить целую часть десятичного числа на основание, пока десятичное число не станет равно нулю.
-Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.
Дробная часть:
-Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
-Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
Пример:
:
44 делим на 2. частное 22, остаток 0
22 делим на 2. частное 11, остаток 0
11 делим на 2. частное 5, остаток 1
5 делим на 2. частное 2, остаток 1
2 делим на 2. частное 1, остаток 0
1 делим на 2. частное 0, остаток 1
Частное равно нулю, деление закончено. Теперь записав все остатки снизу вверх получим число 
