Лабораторная работа № 4
Аппроксимация функции одной переменной
Цель работы
Научиться работать с сетью прямой передачи сигнала, функция newff [1]. Разобраться с алгоритмом обратного распространения ошибки.
Краткие теоретические сведения
В лабораторной работе рассматривается нейронная сеть с прямой передачей сигнала (с прямой связью) [2], то есть сеть, в которой сигналы передаются только в направлении от входного слоя к выходному, и элементы одного слоя связаны со всеми элементами следующего слоя. Важнейшим для реализации нейронных сетей является определение алгоритма обучения сети.
В настоящее время одним из самых эффективных и обоснованных методов облучения нейронных сетей является алгоритм обратного распространения ошибки, который применим к однонаправленным многослойным сетям. В многослойных нейронных сетях имеется множество скрытых нейронов, входы и выходы которых не являются входами и выходами нейронной сети, а соединяют нейроны внутри сети, то есть скрытые нейроны. Занумеруем выходы нейронной сети индексом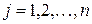 
, а обучающие примеры индексом 
. Тогда в качестве целевой функции можно выбрать функцию ошибки как сумму квадратов расстояний между реальными выходными состояниями 
нейронной сети, выдаваемых сетью на входных данных примеров, и правильными значениями функции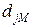 
, соответствующими этим примерам. Пусть 
– столбец входных значений, где i =1,2,.., n. Тогда 
– выходные значения, где j =1,2,…, m. В общем случае n ≠ m. Рассмотрим разность 
, где 
– точное (правильное) значение из примера. Эта разность должна быть минимальна. Введем расстояния согласно евклидовой метрике, определив норму
. (1)
Пусть целевая функция имеет вид
. (2)
Коэффициент ½ выбран из соображений более короткой записи последующих формул. Задача обучения нейронной сети состоит в том, чтобы найти такие коэффициенты 
, при которых достигается минимум 
(Е 
0).
На рис. 1 показана архитектура нейронной сети с прямой передачей сигнала.
|
| Рис. 1. Схема архитектуры нейронной сети с прямой передачей сигнала |
Здесь приняты обозначения, используемые в [1], а именно,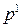 
‑ вектор входа, 
, 
‑ матрицы весов входа и выхода,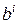 
‑ смещение, 
‑ выход слоя, 
‑ выход сети, tansig (гиперболическая тангенциальная), purelin (линейная) ‑ соответствующие функции активации.
Веса и смещения определяются с помощью алгоритма обратного распространения ошибок [3].
Обучение сети обратного распространения требует выполнения следующих операций:
1. Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети.
2. Вычислить выход сети.
3. Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары).
4. Скорректировать веса сети так, чтобы минимизировать ошибку.
5. Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня.
